1 Версия
Метод простой итерации. Уравнение f(x)=0 преобразуют к виду удобному для организации итерации: x=(x), при этом функция (x) называется итерационной функцией. На отрезке локализации [a,b] выбирается начальное приближение x=x0 и вычисляется x1=(x0). Продолжая этот процесс имеем:
.
Если существует , то получаем равенство: где - корень. Метод сходится при , а при - расходится.
Критерий окончания:
Метод касательных (метод Ньютона). Выбирается точка x0[a,b] и в ней проводится касательная к графику функции y=f(x) и за новое приближение x1 принимается точка, в которой касательная пересекает ось OX и т.д. В итоге получаем итерационную формулу Ньютона:
(2.6)
Необходимым и достаточным условием сходимости метода Ньютона на отрезке локализации x[a,b] являются:
f(x)0, - (необходимое условие); (2.7)
f(x)0 - (достаточное условие);
т.е. знакопостоянство первой и второй производной на отрезке локализации.
2 Версия
Пусть имеется следующая система нелинейных уравнений:
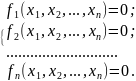(6.5)
Как
уже отмечалось выше, для одной переменной
метод Ньютона использует замену искомого
уравнения уравнением прямой или, как
еще говорят, производит линеаризацию
исходного уравнения. Пусть имеется k
- ое приближение:
.
Разложим левые части системы уравнений
в ряд Тейлора и учтем только линейные
члены:
(6.6)
где
,
i=1,2,...,n; а
частные производные вычисляются в точке
k-го приближения: x1=x1(k),
x2=x2(k),...,xn=xn(k).
Заменим в исходной системе нелинейные функции fi(x1,x2,...,xn) на правые части этих приближенных равенств, которые являются линейными функциями относительно переменных xi, i=1,2,...,n. В итоге получим следующую систему линейных уравнений относительно переменных xi, i=1,2,...,n:
(6.7)
Из
этой системы можно определить значения
xi, i=1,2,...,n
и вычислить значения k+1-приближения:
.
Данная система уравнений представляют
собой метод Ньютона для системы нелинейных
уравнений.
Определитель этой системы называется якобианом.
. (6.8)
Для существования решения якобиан должен быть отличен от нуля для каждого шага итерации.
Критерий
окончания.
Итерационный процесс продолжается до
тех пор, пока не выполнятся условия:
,
для всех i=1,2,...,n.
Обусловленность задачи численного дифференцирования
Так как величина y в формуле (2.10) является абсолютной предельной погрешностью входных данных, а (y)- абсолютной предельной погрешностью результата, то согласно определения абсолютного числа обусловленности для задачи численного дифференцирования из (2.10) имеем:
=(y)/y=1/h,
т.е. задача плохо обусловлена, т.к. при при h0 число обусловленности стремится к бесконечности.
Экзаменационный билет № 26
Арифметические операции над числами с плавающей запятой. Особенности «машинной» арифметики
С целыми числами арифметические операции сложения, вычитания и умножения выполняются точно.
При сложении и вычитании сначала производится подготовительная операция, называемая выравниванием порядков. В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков операндов. После каждого сдвига порядок увеличивается на единицу. В результате выравнивания порядков одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются или вычитаются. В случае необходимости полученный результат нормализуется путем сдвига мантиссы результата влево. После каждого сдвига влево порядок результата уменьшается на единицу.
При умножении двух нормализованных чисел их порядки складываются, а мантиссы перемножаются
При делении двух нормализованных чисел из порядка делимого вычитается порядок делителя, а мантисса делимого делится на мантиссу делителя. Затем в случае необходимости полученный результат нормализуется
Задача одномерной минимизации. Глобальный и локальный минимум. Унимодальные функции
Задача нахождения минимума функции f(x), x[a,b] состоит в нахождении такой точки [a,b], что
(2.1)
Пусть задана функция f(x) на отрезке [a,b]. Точка [a,b] называется точкой глобального минимума, если для всех x[a,b] выполняется условие:
(2.2)
Точка называется точкой локального минимума, если существует - окрестность этой точки, что выполняется условие:
(2.3)
Если
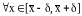выполняется условие
то говорят, что
является точкой строгого локального
минимума.
Унимодальные
функции. Если
на отрезке [a,b]
определена функция f(x)
с одной точкой локального минимума
и при этом для всех
<
функция строго убывает,
,
а для всех
>
функция строго возрастает
,
то такая функция называется унимодальной.
Правило Рунге для оценки погрешности численного интегрирования
См. билет 6
Экзаменационный билет № 27
Виды матриц при решении систем линейных алгебраических уравнений (7 баллов).
См. билет 14
Обусловленность задачи минимизации. Интервал неопределенности точки минимума. Метод прямого поиска
Обусловленность
задачи минимизации. Погрешность
определения точки минимума
связана с предельной абсолютной
погрешностью вычисления значения
функции в точке
следующим образом:
(2.4)
где
- число обусловленности задачи минимизации.
Отсюда следует, что погрешность в
определении x увеличивается в
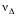по сравнению с погрешностью вычисления
функции
.
Так как при
имеем
,
то задача минимизации является плохо
обусловленной.
Так
как точность расчетов точки минимума
не может быть выше погрешности
,
то имеем
.
оптимальный
пассивный поиск. На
отрезке [a,b]
задается
последовательность точек x0,x1,...,xn,
таких,
что xk=x0+kh,
k=1,...,n;
x0=a,
xn=b.
В
этих точках вычисляется значение функции
f(xk).
За точку минимума
принимается
та точка
xk,
для которой выполняется соотношение:
.
Следовательно:
Отсюда
Погрешность интерполяции
См. «Точность интерполяции»
Погрешность интерполяции Rn(x) зависит от числа узлов n и равна:
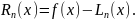(2.11)
В узлах интерполяции погрешность равна нулю. Ее величина зависит от вида аппроксимирующей функции и вычисляется по следующей формуле:
(2.12)
где неизвестная точка на отрезке [x0,xn].
Для равномерного распределения узлов, когда xi-xi-1=h, для всех i=1,2,...,n (равномерная сетка с шагом h) можем записать:
