Фундаментальная система решений однородной системы уравнений

Фундаментальная система решений – это множество линейно независимых векторов  , каждый из которых является решением однородной системы, кроме того, решением также является линейная комбинация данных векторов  , где   – произвольные действительные числа.

Количество векторов   фундаментальной системы рассчитывается по формуле:

Однако в практических заданиях гораздо удобнее ориентироваться на следующий признак: количество векторов   фундаментальной системы равно количеству свободных неизвестных.

Представим общее решение  Примера №3   в векторной форме. Свободная переменная в данном случае одна, поэтому фундаментальная система решений состоит из единственного вектора  . Как его найти? Для этого свободной переменной нужно придать произвольное ненулевое значение. Проще всего, конечно же, выбрать   и получить:  .

Координаты вектора   должны удовлетворять каждому уравнению системы, и будет не лишним в этом убедиться.

Ответ следует записать в виде линейной комбинации векторов фундаментальной системы. В нашей ситуации линейная комбинация состоит из одинокого слагаемого. Общее решение однородной системы я буду обозначать через вектор   (подстрочный индекс расшифровывается «Общее Однородной»).

Ответ: общее решение:  , где   (любое вещественное число)

Придавая параметру   различные действительные значения, можно получить бесконечно много частных решений, например, если  , то вектор частного решения однородного уравнения («Частное Однородной») равен: , то есть набор переменных   удовлетворяет каждому уравнению системы.

Это мы рассмотрели традиционный способ построения фундаментальной системы в так называемом нормальном виде – когда свободным переменным придаются исключительно единичные значения. Но правила хорошего математического тона предписывают избавляться от дробей, если это возможно. Поэтому в данном случае можно взять   и из общего решения системы   получить вектор с целыми координатами: 

И тогда ответ запишется в эквивалентной форме: , где   (любое вещественное число)

Оба варианта ответа правильны, однако чайникам я всё-таки рекомендую классику жанра.

Поблагодарим задачник Рябушко за предоставленные примеры и перейдём к более основательным системам:

Пример 4

Решить однородную систему линейных уравнений

Ответ записать с помощью фундаментальной системы решений

Самостоятельно, plz. Примерный образец оформления в конце урока.

Закинем в копилку знаний ещё один полезный факт:

Взаимосвязь решений неоднородной и соответствующей однородной системы уравнений

Представьте двух близких родственниц: неоднородную систему (у которой хотя бы одно число правой части отлично от нуля) и такую же систему – только справа одни нули (то бишь, однородную систему). Нетрудно предположить, что если системы отличаются лишь столбцом свободных членов, то между их решениями должна существовать тесная связь. И это действительно так! Материал целесообразнее рассмотреть на конкретной задаче, которая, как и все другие, взята из реальной контрольной работы:

Пример 5

Дана система линейных алгебраических уравнений

Требуется:

1) найти общее решение;

2) используя результат предыдущего пункта, найти общее решение соответствующей однородной системы и записать его в векторной форме.

Решение: по условию дана обычная неоднородная система уравнений, и первая часть не отличается новизной:

1) Запишем расширенную матрицу системы (не зеваем нолик в третьей строке) и с помощью элементарных преобразований приведём её к ступенчатому виду:

(1) Ко второй строке прибавили первую строку, умноженную на –1. К третьей строке прибавили первую строку, умноженную на –3. К четвёртой строке прибавили первую строку, умноженную на –4.  (2) Последние три строки одинаковы, две из них удалили.

Обратным ходом метода Гаусса получим общее решение:   – базисные переменные;  – свободные переменные.

Выразим базисные переменные через свободные переменные. Из 2-го уравнения:  – подставим в 1-е уравнение:

Общее решение неоднородной системы  обозначим через    («Общее Неоднородной»).

Ответ: 

2) Во второй части задания требуется найти общее решение   такой же, только однородной системы  , причём по условию необходимо использовать ответ предыдущего пункта.

Выполнять элементарные преобразования заново, разумеется, не нужно.

Правило: общее решение неоднородной системы   равно сумме общего решения соответствующей однородной системы   и какого-либо частного решения неоднородной системы  :

Откуда легко выражается общее решение нашей однородной системы:

Найдём какое-нибудь частное решение   неоднородной системы. Проще всего взять нулевые значения свободных переменных  :

Таким образом, общее решение соответствующей однородной системы:

Представим   в векторной форме. Поскольку у нас две свободные переменные, то фундаментальная система решений будет состоять из двух векторов.

Пойдём классическим путём:

Рассмотрим пару значений свободных переменных   и получим первый вектор:  – координаты данного вектора удовлетворяют каждому уравнению однородной системы (всегда желательна проверка!).

Теперь рассматриваем пару   и получаем второй вектор:  – координаты данного вектора также удовлетворяют каждому уравнению однородной системы (тоже проверяем!).

И вообще – любая линейная комбинация векторов фундаментальной системы  , где   – произвольные действительные числа, является решением данной системы:

Ответ:  , где 

Иными словами, если взять два любых вещественных числа, например,  , то получится вектор частного решения однородной системы: ,  то есть набор   удовлетворяет каждому уравнению однородной системы.

Если хотите избежать дробей, то при нахождении вектора   следует выбрать значения   и получить второй вектор в виде: В этом случае ответ запишется в эквивалентной форме: , где 

Порядком многих я, наверное, подзапутал, но коль скоро задание не придумано, то его нельзя было обойти стороной.

Более распространённая тема для самостоятельного решения:

Пример 6

Дана однородная система

Найти общее решение и записать ответ с помощью векторов фундаментальной системы. В образце решения завершающим элементарным преобразованием я уже потихоньку начинаю приобщать вас к методу Гаусса-Жордана.

Чтобы окончательно закрепить алгоритм, разберём финальное задание:

Пример 7

Решить однородную систему, ответ записать в векторной форме.

Решение: запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:

(1) У первой строки сменили знак. Ещё раз заостряю внимание на неоднократно встречавшемся приёме, который позволяет существенно упростить следующее действие.

(1) Ко 2-й и 3-й строкам прибавили первую строку. К 4-й строке прибавили первую строку, умноженную на 2.

(3) Последние три строки пропорциональны, две из них удалили.

В результате получена стандартная ступенчатая матрица, и решение продолжается по накатанной колее:

 – базисные переменные;  – свободные переменные.

Выразим базисные переменные через свободные переменные. Из 2-го уравнения:

 – подставим в 1-е уравнение:

Таким образом, общее решение:

Поскольку в рассматриваемом примере три свободные переменные, то фундаментальная система содержит три вектора.

Подставим тройку значений   в общее решение и получим вектор  ,  координаты которого удовлетворяют каждому уравнению однородной системы. И снова повторюсь, что крайне желательно проверять каждый полученный вектор – времени займет не так много, а от ошибок убережёт стопроцентно.

Для тройки значений   находим вектор

И, наконец, для тройки   получаем третий вектор:

Ответ:  , где 

Желающие избежать дробных значений могут рассмотреть тройки   и получить ответ в эквивалентном виде:

К слову о дробях. Посмотрим на полученную в задаче матрицу   и зададимся вопросом – нельзя ли упростить дальнейшее решение? Ведь здесь мы сначала выразили через дроби базисную переменную  , потом через дроби базисную переменную  , и, надо сказать, процесс это был не самый простой и не самый приятный.

Второй вариант решения:

Идея состоит в том, чтобы попытаться выбрать другие базисные переменные. Посмотрим на матрицу и заметим две единицы в третьем столбце. Так почему бы не получить ноль вверху? Проведём ещё одно элементарное преобразование:

(4) К первой строке прибавили вторую строку, умноженную на –1.

Здесь базисные переменные   легко и практически мгновенно выражаются через свободные переменные  :

По существу, мы применили метод Гаусса-Жордана, который как раз и направлен на скорейшее получение базисного решения посредством дополнительных элементарных преобразований.

В результате общее решение: 

Последовательно выбираем в качестве значений свободных неизвестных тройки 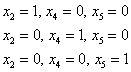и подстановкой их в   получаем соответствующие векторы фундаментальной системы:

Не забываем проверить координаты каждого вектора!

Ответ: общее решение: