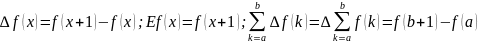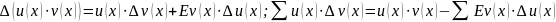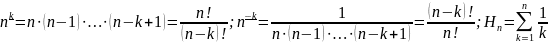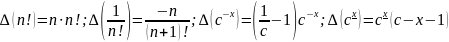Конкретная математика. Лекция 3. Вычисление конечных сумм, часть 2. Метод приведения.
Метод
приведения – это ещё один эффективный
метод вычисления сумм. В ряде случаев
он бывает эффективнее метода репертуаров
или метода неопределённых коэффициентов,
позволяя найти результат гораздо быстрее
и проще. Обозначим искомую сумму как
Sn:
.
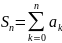Теперь перепишем сумму Sn+1 двумя способами, выделяя первый и последний члены:
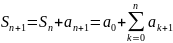(3.1)
Теперь можно заняться последней суммой и попытаться выразить её через Sn – если это получится, то в итоге будет уравнение, решением которого и будет искомая сумма.
Примеры применения метода приведения:
вычисление суммы геометрической прогрессии
. Согласно (3.1):
вычисление суммы
.
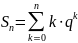Применяем (3.1) здесь:
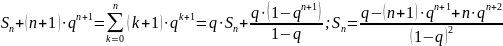
вычисление сумм степеней натуральных чисел
. Здесь (3.1) напрямую не даёт нужного
результата, но нужный эффект даёт
использование Sn+1(q+1):
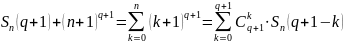
Например, в случае суммы квадратов чисел:
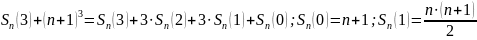
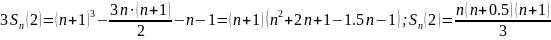
Метод усложнения и упрощения.
В этом методе одинарная сумма заменяется кратной, после чего слагаемые перегруппировываются так, что вычисления заметно упрощаются. Обычно используют:
(3.2)
С помощью них можно получить, например, следующие формулы:
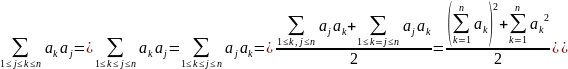
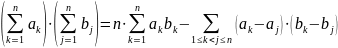(3.3)
Равенство (3.3) получается путём следующих преобразований:
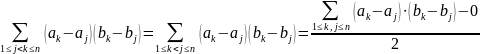
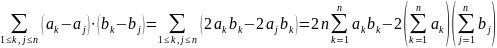
Из (3.3) следуют неравенства Чебышева для сумм:
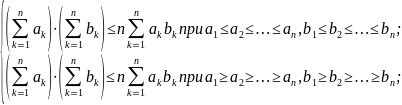(3.4)
Примеры применения метода усложнения и упрощения:
Обозначим за Нn гармоническое число:
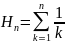и посчитаем
:
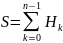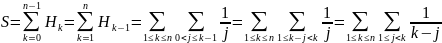
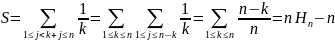
Вычислим сумму квадратов натуральных чисел:
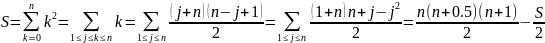
Метод конечных разностей.
Введём операторы конечной разности ∆ и сдвига Е. Они превращают функции в другие функции:
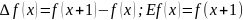(3.5)
Введём
следующие обозначения. Убывающей
факториальной степенью
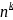назовём выражение:
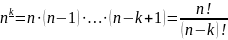(3.6.1)
Соотвественно
возрастающей факториальной степенью
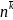назовём аналогичное выражение:
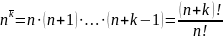(3.6.2)
Аналогично можно определить обратные степени:
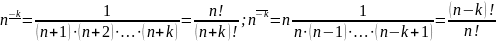(3.7)
Из них особенно удобны убывающие степени потому, что для них верно:
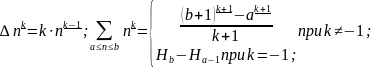(3.8)
Это позволяет, в частности, вычислять суммы степеней натуральных чисел намного проще, чем это делали мы выше. Кроме того, оперирование конечными разностями заметно облегчает вычисление сумм благодаря существованию формул конечной разности произведения функций (3.9) и следующей из неё формулы интегрирования по частям (3.10):
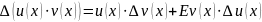(3.9)
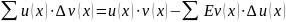(3.10)
Формулу суммирования по частям можно записать и в более подробной форме:
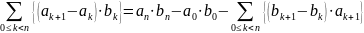
Также очень полезным свойством относительно этих операторов обладает функция 2х и cx:
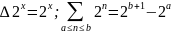(3.11)
Аналогично
для функции cx:
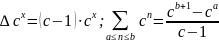(3.12)
Основные формулы для суммирования.
Количество
перекладываний для ханойской башни:
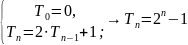
Разрезание
плоскости прямыми:
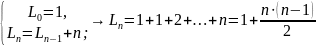
Случай многомерного разрезания в k-мерном пространстве:
Нахождение последнего при исключении каждого второго из круга:
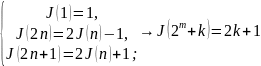
Прогрессии:
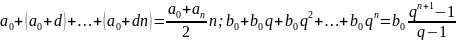
Метод суммирующего множителя:
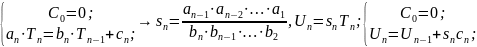
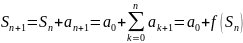– метод приведения
Суммы, получаемые путём перестановки слагаемых:
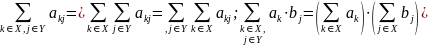
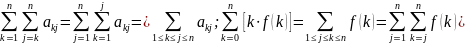
Метод конечных разностей.
