9.3 Орталық симметриялық өрістегі бөлшектің қозғалысы.

Орталық симметриялық өріс деп – потенциалдық энергиясы центрінен қандай да бір центрден қашықтыққа тәуелді болатын өрісті айтады.

Бөлшектің мұндай қрісте әсер ететін күш радиусынынң бойында бағытталады. Сондықтан классик механика толық механикалық энергиямен қатар импульс моментіде сақталады.

Стационар күйлерді қарастыру үшін ортылық күштік өрісте қозғалған микробөлшек үшін Шредингер теңдеуін қарастыру керек. Қріс симметриялық болғандықтан, сфералық координатада қарастырамыз.

Яғни, Ĥ (12)

Мұндағы, Ĥ=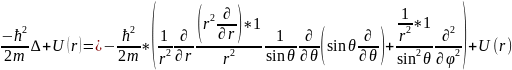 = 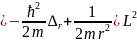+U(r) (13)

Мұндағы, 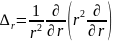(14)

Егер (11,12,13) теңдеулерге мұқият қарайтын болсақ, Ĥ, , операторы бір-біріне коммутация жасайтындығы көрінеді. (13) өрнекті айнымалыларға бөлу әдісімен қарастырайық:

(15)

Мұндағы, R(r) - тек радиус векторға тәуелді радиал функция.

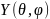- тек бұрыштық шамаларға тәуелді шама .

12-ші өрнекті 15-ші өрнекке қойсақ: 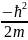Y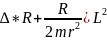 *Y+URY=ERY (16)

15-ші теңдеуді:

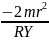
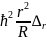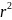*R-2m U +2m E =

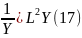
17-ші өрнектің теңдік белгісінің сол жағы тек r-ге тәуелді, ал оң жағы ψ-ке тәуелді. Математикада мұндай теңдік орындалу үшін олардың әр қайсысын қандай да бір тұрақты шамаға теңестіріп шығарады. Біз ондай шаманы λ-деп белгілейік. Сонда, бастапқы Шредингер тіңдеуі екі теңдеуге жіктеледі.

(18) *R-2m U +2m E (19)

18-ші теңдеу яғни 1-ші бөлігі импульс моменті өрнегі операторының квадраты, ал сол бізге белгілі:

λ =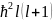 (20)

20-шы өрнекті ескере отырып, 19-шы теңдеуді былайша жазуға болады.

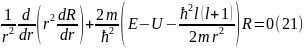
Бұл 21-ші теңдеу радиал теңдеуі деп аталады. Ол бір өлшемді Шредингер теңдеуіне яғни өрісте қозғалған бөлшектің теңдеуіне сәйкес келеді.

U+

№10лек

10.1Сутегі атомының ионизация энергиясы шамамен 13,6 эВ бұл өз кезегінде тыныштық энергиясы 0,51 МэВ болатын электронның энергиясынан айтарлықтай кіші. Олай болса, сутегі атомының есебі релятивистік емес тұрғыдан қарастыруға болады. Яғни, сандардың сақталу заңы орындалады және Шредингердің релятивистік емес теңдеуі қолданылады. Кейбір магниттік әсерлерді ескермеген жағдайда, сутегі атомындағы электрон ядроға тартылу әсерінен Кулондық өрісте қозғалады деп қарастырылады. Яғни электронның потенциалдық энергиясы:

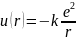(1)

Мұндағы: 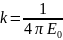→ Кулон тұрақтысы.

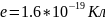→ элементар заряд.

Өріс-орталық симметриялық. Сутегі атомының есебін шығарарда ядролық массасы электрон массасынан жуық шамамен 2000 есе үлкен болғандықтан, ядроны тыныштық күйде тұрады деп қарастыруға болады. Бұл жағдайда электронның массасын екі дене есебіндегі келтірілген массаға алмастырып жазуға болады.

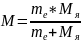(2)

Сондықтан, сутегі атомының есебінде Шредингер теңдеуін электронның энергиясы,ал күй функциясы электронның ядроға байланысты жүйедегі қозғалысын сипаттайды. Бұл жағдайда өрістің эффективті потенциалдық энергиясы мына түрде жазылады:

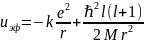(3)

Радиал теңдеуді шешу?

Радиал теңдеу мына түрде жазылады:

(4)

Теңдеуімізді қарапайымға келтіруіміз үшін, өлшем бірліксіз мынадай шамаларға ауысайық:

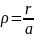, мұндағы: 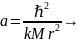Бор радиусы деп аталатын тұрақты шама.

орнына қойсақ а-ның:

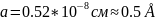
Келесідей белгілеулер енгізейік:

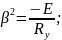мұндағы: 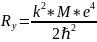(5)

, өлшем бірлігі энергияның өлшем бірлігімен бірдей және жуық шамамен:

→атомдағы электронның энергиясы.

Осы белгілеулерді (4) қойсақ:

(6)

(6) өрнек 2ші ретті диференциалдық теңдеу, сутегі атомы үшін есептер радиал өрнегінің теңдеуі.

Ол теңдеудің шешімі мына түрде :

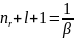( 7)

Мұндағы 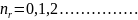радиал кванттық сан.

Оны әдетте кванттық санмен алмастырады.

(8)

n-бас кванттық сан.

(8) өрнекті ескеріп, сутегі атомының энергиясын ескеріп:

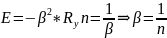
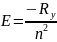(9)

10.2

Сутегі атомының есебінің жалпы шешімі (9) өрнекте көрсетілді. Сол алынған шешімнің негізінде электронның стационар күйін толық сипаттауға болады. Электронның стационар күйлері n,l,m- кванттық сандар көмегімен анықталады. Бұл кванттық сандар көмегімен энергиясын, импульс моментін, импульстің моменттік проекцияларын анықтауға болады. Яғни:

10.3

Сутегі тәріздес жүйелер деп-электростатикалық әсерлесу арқылы байланысатын екі әр аттас зарядталған бөлшектен тұратын барлық жүйені айтады. Сутегі тәріздес жүйеге бір электроны бар, барлық атомдардың оң иондары, позитрон (электрон мен позитроннан тұратын жүйе ), антиатомдар (антипротон мен антипозитроннан тұратын жүйе) мионий (протон мен мион тұратын жүйе) т.б . Сутегі тәріздес жүйелерді бөлшектердің салыстырмалы қозғалысы массасы келтірілген масса (М)-ға тең орталық симметриялы тартылыс өрісінде қозғалады деп қарастырылады. Мұндай бөлшектің потенциалдық энергиясы:

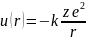(10)

Сутегі тәріздес жүйе үшін радиал теңдеуді жазайық: 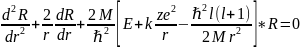(11)

Бұл теңдеу сутегі атомы үшін жазылған теңдеуден (4), тек тұрақтылардың мәндерімен ерекшеленеді.Егер келесідей белгілеулер енгізсек:

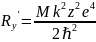; ; -сутегі атомының тәріздес (11) теңдеуіміз (6) теңдеуге айналады. Ал (6) теңдеудің шешімі белгілі. Олай болса сутегі тәріздес атомдар үшін сутегі атомының есебінің нәтижесі толығымен сәйкес келеді.Сутегі тәріздес атомдардың энергия деңгейлері: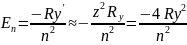

n,l,m- кванттық сандардың мағынасы. Сутегі атомы үшін жазылғандардан өзгермейді.

12-лекция ЭЛЕКТРОН СПИНІ ТУРАЛЫ ГИПОТЕЗА

Көптеген эксперименттердің нәтижелері атомның магниттік моменті тек электрондардың орбитальді магнит моментіне сәйкес болмайтынын көрсетеді.Сондықтан электронның меншікті импульс моменті болады және ол электронның меншікті магнит моментіне пропорционал болады деген болжам жасауға болады.

Электронның меншікті импульс моменті оның спині деп аталады.

Сутегі атомын және сутегі тәріздес жүйені қарастырғанда электрондардың орбитальдық және спиндік магниттік моменттерін өзара әсерлесуін ескеру қажет.Өйткені әсіресе көп электронды атомдарды бұл әсерлесу ескеретіндей үлкен болады.Спинді және орбитальдық әсерлесудің энергиясы үлкен емес сондықтан алдындағы энергетикалық деңгей туралы түсінікке үлкен өзгерістер енгізбейді.Спектрлердің жұқа құрылымдарын қарастырудың нәтижесінде Уленбек және Гаудсмит 1925ж электронның меншікті магниттік және механикалық моменті яғни спиннің болатындығын Шредингер Герлак тәжірбиесінде растайтын еді.Егер біртекті емес магнит өрісі арқылы сутегі атомдарының шоғырын өткізсе негізгі (15) түрдегі 2 шоққа жүктеледі.

Негізгі 1S күйдің орбиталды магниттік моменті 0-ге тең болғанымен электронның спиндік магниттік моментінің болуымен түсіндіреді.

Штерн Герлак тәжірбиесі электронның спиндік магниттік моменттінің проекциясының шамасын табуға мүмкіндік берді.Ол Бордың магнитолінің шамасына тең болды.

Электронның спиннің болуы кеңістіктегі қозғалысына байланысты емес сондықтан спин туралы Шредингер теңдеуінен мағлумат алалмаймыз.Өйткені Шредингер теңдеуі спині жоқ бөлшектер үшін жазылған.

Көп жағдайда көрнекілік үшін электронның масса центрі арқылы өтетін ось маңында айналатын зырылдауық шарик ретінде бейнелейді.Бірақ бұл нұсқа дұрыс деуге келмейді.Бүгінгі таңда электрон құрылымы жоқ нүктелік бөлшек.Сондықтан оның спиндік пайда болуы квантық релятивистік эффект.

Электронның массасы немесе заряды туралы түсінікпен салыстырғанда электронның спині деген түсінік таза кванттық түсінік болып табылады яғни классикалық баламасы жоқ түсінік.Бүгінгі таңда тек электронда ғана емес басқа да элементар көп бөлшекте де спиннің болатындығын дәлелдеген.

12.2

Кванттық механикада динамикалық айырмалар өздеріне сәйкес оператор арқылы енеді. Спинді сипаттау үшін спин операторы қолданылады және оның проекциялары 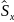, , 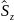мына түрде қолданылады.Спиндік момент үшін орбитальді импульс моменті сияқты келесі қатынастар орындалады. ;

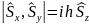(1)

Олай болса коммунтация ережесіне сәйкес келесідей квантталу шартын жазуға болады.

S=h (13.2)

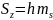(13.3)

S –спиндік кванттық сан деп атал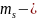ады. спиндік проекцияның кванттық саны деп аталады

Спиндік сан мен спиндік проекцияның 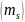саны арасында келесідей қатынас орындалады.

2S+1=2; 2S=1; S=

Олай болса

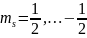
Сонымен электронның спиндік мех-қ моменті келесі өрнекпен жазылады

S=h ; S=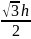 (13.4) Ал oz өсіне проекциясы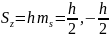

Спин тек электронға ғана емес сондай ақ басқа элементар бөлшектерге тиесілі.

Кейбір элементарлы бөлшектерді қарастырайық.Мыс, Спин жартылай бүтін яғни 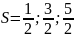т.б бөлшектер бір класқа біріктіріліп фермиондар деп аталады. Спині бүтін сан яғни S=0,1,2… болатын элементар бөлшек базондар деп аталады.Барлық микробөлшектер үшін(12.2),(12.3) өрнектері орындалады.Сутегі атомының энергиясы магниттік әсері ескерілмеген жағдайда жуықтап алғанда спинге тәуелді болмайды деп қарастырылады.Қорыта айтқанда сутегі есебінің шешімінің нәтижесінде сутегі атомын Бордың жартылай классикалық, жартылай кванттық теориясы негізінде қарастыруға болады. Бірақ Шредингердің теңдеуіне негізделген теорияның көмегімен қарастырғанда атомның құрылымы мен қасиеттері туралы толығырақ ақпарат алуға мүмкіндік береді.