8.1 Физикалық шамалардың орташа мәндерінің уақыт өтуімен өзгеруі, Эренфест теңдеуі

Классикалық механиканың белгілі шамалардың уақыт бойынша өзгеру заңы үлкен маңызға ие болады. Мысалы: Классикалық механиканың негізгі теңдеуі

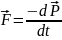
Немесе: Күш маментінің формуласы

Айналмалы қозғалыстың негізгі теңдеуі.

Микробөлшектер әлемінде де физикалық шамалардың уақыт бойынша өзгеру заңдарын қарастырайық . Микробөлшектер әлемінде жалпы жағдайда бөлшектің күйін сипаттайтын шаманың нақты мәнін анықтау мүмкін болмағандықтан оның орташа мәнінің уақытқа тәуелділігін қарастырайық. Микробөлшектің күйін сипаттайтын шаманың орташа мәнінің уақытқа тәуелділігі жүйенің куйі стационар болмаған жағдайда мына өрнекпен анықталады.

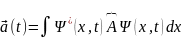
Шаманың орташа мәніннен уақыт бойынша толық деференциял табайық.

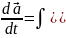)dx

Физикалық шамалардың орта мәндерін уақыт бойынша өзгерісін.

Ол өрнектен операторы 0-ге тең боладыдеп орташа мән тұрақты болады. Яғни Кванттық механикада ол былайша жазылады А операторы

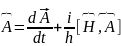
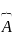операторы уақытқа тәуелді болмаса шама тұрақты болу үшін А және өзара камутативті болуы жеткілікті.

4-өрнек немесе оған эквивалентті 5-қатынас математикалық тілмен айтқанда физикалық шамалардың уақыт бойынша өзгеруін сипаттайтын сондықтан сол өрнектер кванттық механикада қозғалыс теңдеулері депте аталады. Егер физикалық шама уақытқа тәуелді болмаса.

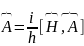
Бұл өрнек қозғалыс теңдеуінің Гейзенберг түрінде жазылуы деп аталады және кванттық механиканың негізін қалайтын Шредирингтер теңдеуінің орнын баса алады.

(5*) өрнектің мағынасын ашу үшін келесі өрнектерді яғни кванттық механикадағы негізгі операторлар координатасы мен импулсы ушін жазамыз.

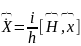(6)

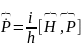(7)

6-7 теңдеулер Гамелтонның классикалық теңдеулерімен салыстыруға болады. Бұл теңдеулер гамелтонның кванттық механиканың теңдеулері деп аталады.

М: U(x,y,z,t) күштік өрістер қозғалысын қарастырайық.

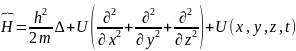
8-өрнек –6 қойсақ ол үшін 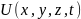және 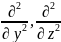осы операторлар .

Олай болса теңдеу камутация жасайдыма соны анықтау жеткілікті.

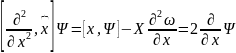
Олай болса: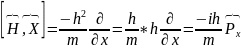

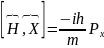
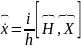
8.2

Физиканың басқа бөлімдеріндегі сияқты кванттық механикада да микробөлшектің күйін немесе микробөлшектер жүйесінің күйін және оның өзгеруін сипаттайтын кейбір динамикалық шамалардың сақталу заңдары маңызды роль атқарады. Ондай сақталу заңдарына физиканың барлық бөлімінде қолданылатын әмбебап шамалар:энергияның, импульстің және импульс моментінің сақталу заңдары жатады. Кванттық механикада неме микродүниеде бұл сақталу заңдарына шаманың жұптылығының сақталу заңы деп аталатын , тек кванттық механикаға тән сақталу заңын қосып айтуға болады.

Кванттық механикада сақталу заңдарына Щредингер теңдеуінің көмегімен қарастырылады. Кез-келген физикалық шаманың операторы үшін:

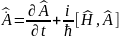(17)

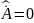және a = const шартын қанағаттандырғанда физикалық шамалардың нақты мәндерінің сақталу шарттарын қарастырайық:

1) Энергияның сақталу заңы: Гамильтон операторы уақытқа тәуелді болуы да, болмауы да мүмкін стационар өрістер үшін:

E = const (18)

(18) өрнектен мынадай қортынды жасалады. Стационар өрісте микробөлшектің энергиясы тұрақты болады.

2) Импульстің сақталу заңы: бөлшек импульсінің операторы

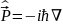
уақытқа тәуелді емес және еркін бөлшек үшін Гамильтон операторымен коммутация жасайды. Олай болса:

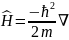(19)

(19)өрнек импульстің сақталу заңы және одан мынадай қортынды жасайды: Еркін бөлшектің импульсі өзгермейді, тұрақты болады, басқаша айтқанда тұйықталған жүйеде, микробөлшектер жүйесінің үйкелісі өзгермейді тұрақты болады.

3) Импульс моментінің сақталу заңы:

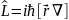(20)

(20) өрнек уақытқа тәуелді емес және еркін бөлшек үшін Гамильтон операторымен коммутация жасайды . Олай болса еркін бөлшектің импульс моменті өзгермейді тұрақты болады яғни тұйықталған жүйедегі импульс моменті тұрақты болады.

8.3.

Кеңістіктің біртектілік және изотроптылық қасиеттерімен қатар оның тағы да бір қасиеті симметриялылығы. Кеңістіктің симметриялылығымен қатар яғни

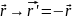
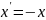
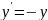
Инверция операциясы екі топтан тұрады:

1. Айнада шағылу

2. Оны 180 -градусқа бұру

Мыс: А нүктесі үшін инверция операциясын қолдануды көрсетейік

Сонда, А нүктесінің координатасына нүктесінің координатасы инверция болып табылады. координаталарын түрлендіруді екі түрлі жүзеге асыруға болады.

1. Жүйені ығыстыру салдарынан

2. Координатаның осьтерін өзгерту салдарынан

2-тәсілге мысал ретінде мына сүретті келтіруге болады:

Инверция кезінде жүйенің физикалық күйі өзгермейді деп қарастырайық. Түрлендіргенге дейінгі жүйенің 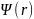функциясымен сипатталсын. Ал, түрлендіргеннен кейінгі күйі 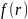толқындық функциямен сипатталсын. Онда инверцияның ережесіне сәйкес:

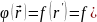
Инверция операторын деп белгілейді. Сонда

Олай болса +-

Егер инверсия операторы Гамильтон операторымен коммутация жасайтын болса, қандай да бір физикалық шаманың сақталу заңы орындалады. Бұл сақталу заңы жұптылықтың сақталу заңы деп аталады. Инверция операторы үшін:

(22) өрнектің екі жағына да инверция операторын тағы да қолданайық:

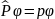
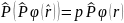
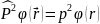(23)

Инверция операторының анықтамасына сәйкес оны кез-келген функцияны екі рет қолданғанда бастапқы функцияны аламыз.

(23)-(24) – өрнектерді салыстырсақ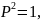 ал

Инверция операторының меншікті мәндері: +1 және -1

Бұл екі сан жаңа физикалық шаманың мәндері болып табылады және микробөлшек күйінің жұптылығын сипаттайды.

ЛЕКЦИЯ № 9.

Тақырып: Орталық симметриялық өрістегі қозғалыс.

9.1. Импульс моменті операторының және оның проекцияларының қасиеттері.

Макраскопиялық денелердің айналмалы қозғалысын сипаттайтын негізгі шамалардің бірі импульс моменті. Бұл шама әсіресе кванттық механикада микробөлшектердің немесе олардың жүйелерінің күйін анықтауға энергиямен бірге шешуші шама болып табылады.

Атом құрылуын тереңірек зерттеу үшін импульс моментінің кванттық қасиеттерін білу шарт. Импульс моментінің операторы мына түрде жазылады:

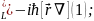
Импульс моменттерінің операторлары декарттық координаттарда остеріне проекциялары:

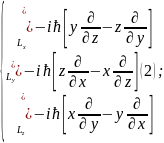
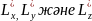операторлары үшін келесі қатынастар орындалады:

Бұл операторлар өзара коммутация жасамайтындықтан:

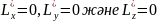жағдайлардан басқа уақытта мына қатынас орындалады:

Импульс моментінің операторларының квадраты оның проекцияларының операторларына коммутация жасайды.

Бұл импульс моментінің модулінің анықталған күйі болатындығын көрсетеді.

Орталық өрістегі бөлшектің қозғалысын қарастырғанда сфералық координатада қарастырған ыңғайлы. Сфералық координатада:

айнымалыларына тәуелді бөлшектің қозғалысы қарастырылады.

Сфералық координаттарда импульс моментінің проекциялары мына турде қарастырылады:

9.2 ^ және операторларының меншікті мәндері мен меншікті функциясы.

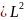және өзара коммутация жасайтын операторлар ортақ меншікті функцияға ие болады. Осы функцияны табу үшін келесі теңдеуді шешеміз:

^ ψ(r)=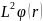 (6)

Бұл теңдеу сфералық координаталарда:

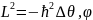(7)

Мұндағы, ( )+ (*)

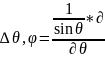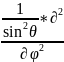Олай болса 6-шы теңдеу келесі дифференциалдық теңдеуге айналады:

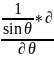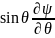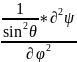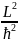( )+ = ψ; (8)

8-ші өрнек математикада белгілі Лаплас теңдеуінің сфералық координата жазылған түрі болып табылады. Ол толық шешілген, сондықтан онығ жауабы дайын күйде жазылады.

(9)

Мұндағы, 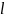=0,1,2, …..

6-шы теңдеу сфералық функциялар (теңдеуі) болып табылады. Оларды 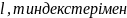белгілейді. Мысалы,

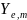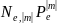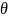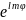( )= (cos ) (10)

Мұндағы, 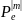(cos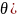 - аргументті cos болатын Лежандра Полилео болып аталады.

Мұндағы, 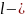азимуталды (орбиталды) кванттық сан. Ал, m-магніттік кванттық сан.

10-ші теңдеудің дербес шешімі мына түрде жазылады:

Ψ= C (11)