42. Нормальное распределение и свойства кривой нормального распределения .

Нормальное распределение является частным (предельным) случаем биномиального распределения, в котором p=q и n→∞. График – симметричная и плавно изменяющаяся кривая, колоколообразная формы. Нормальное распределение отражает характер варьирования мерных непрерывно изменяющихся признаков. Нормальному распределению подчиняется большая часть биологических признаков, так как и их формировании принимает участие великое множество независимых, случайных факторов. Варьирование признака происходит относительно среднего значения. Вероятность нахождения значения биологического признака, подчиняющегося закону нормального распределения, в диапазоне от х до х+∆х, вычисляется по формуле

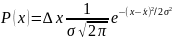. Уравнение плотности распределения дает значение ординат кривой нормального распределения и имеет вид 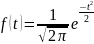где t=(x- /σ – нормированное отклонение значения признака ч от средней (математического ожидания). 42. Вероятность нахождения величины Х в диапазоне от t ₁ до t₂ вычисляют по формуле где t₁=(x₁-x̅)/σ t₂=(x₂-x̅)/σ.

Графически величина P(t) на кривой нормального распределения представлена площадью фигуры, ограниченной с боков перпендикулярами, опущенными на ось абсцисс в точке t₁ и t₂, снизу- осью абсцисс, сверху – отрезком кривой нормального распределения. Вероятность P(t)=[Ф(t₂)±Ф(t₁)]/2 где Ф – значения интегралов вероятностей, найденные в таблице.

Для того, чтобы найти количество вариант р', имеющих значение признака, заключенного в пределах от t₁ до t₂ , необходимо вероятность умножить на объем выборочной совокупности. р'=P(t)n. В случае нормального распределения вероятность нахождения случайной величины в диапазоне x̅±3σ равна 0,9973 (99,73%), то есть практически значения всех вариант статистической совокупности должны лежать в границах x̅±3σ.

Свойства нормального распределения

Рассмотрим основные свойства этого важнейшего распределения.

Свойство 1. Функция плотности нормального распределения определения на всей оси абсцисс.

Свойство 2. Функция плотности нормального распределения больше нуля для любого из области определения ( ).

Свойство 3. При бесконечном увеличении (уменьшении) функция распределения стремится к нулю .

Свойство 4. При функция распределения , заданная функция плотности нормального распределения , имеет наибольшее значение, равное

( 24)

Свойство 5. График функции (рис.9.11 ) симметричен относительно прямой .

Свойство 6. График функции имеет по две точки перегиба симметричные относительно прямой :

( 25)

Свойство 7. Все нечетные центральные моменты равны нулю. Заметим, что используя свойство 7, определяют асимметрию функции по формуле . Если , то делают вывод, что исследуемое распределение симметрично относительно прямой . Если , то говорят, что ряд смещен вправо (более пологая правая ветвь графика или затянута). Если , тогда считают, что ряд смещен влево (более пологая левая ветвь графика рис.9.12 ).

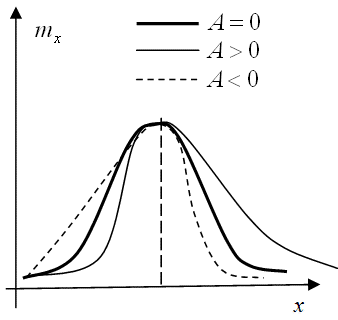
Рис. 9.12. Функция плотности распределения для различных А

Свойство 8. Эксцесс распределения равен 3. Часто на практике вычисляют и по близости этой величины к нулю определяют степень "сжатия" или "размытости" графика (рис.9.13 ). А так как связан с , то, в конечном итоге характеризует степень рассеяния частоты данных. А так как определяет точность измерений (степень рассеянности данных), то становится очевидным, почему в случае повышенной точности измерений, результаты будут группироваться около центра, а в результате кривая будет круче подниматься в центре и резче спадать по мере удаления от среднего (рис.9.13 , ). А тогда с увеличением , т.е. ухудшением качества измерений, рассеяние результатов увеличивается, а кривая принимает более пологий (сглаженный) вид (рис.9.13 , ).

Рис. 9.13.

Кривая нормального распределения носит также название кривой Гаусса (1777 – 1855) – по имени знаменитого немецкого математика, глубоко исследовавшего теорию случайных ошибок и метода наименьших квадратов. В настоящее время теория случайных ошибок измерений является отделом другой, более обширной науки – математической статистики, разрабатывающей рациональные методы и приемы обработки большого количества экспериментальных данных. Эти приемы связаны с современными теориями устойчивости, бифуркаций и катастроф.

Закономерности случайного рассеивания сопровождают появление наиболее характерных, массовых для данной местности, образцов пород, которые хотя и разные по своему виду, текстуре, размеру, испытывают влияние большого количества разнообразных случайных факторов, но при этом подчиняются нормальному закону распределения.

Свойство 9. Форма кривой не изменяется при изменении параметра .

График нормальной функции распределения (22) показан на рис.9.14 .

Рис. 9.14. График нормальной функции распределения