Важнейшие свойства средней арифметической Дополнить!

Средняя арифметическая обладает рядом свойств, которые имеют большое практическое значение:

1. Если х_i = с, где с – постоянная величина, то

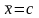
Доказательство: пусть х₁ = х₂ = …= х_n = с

Тогда

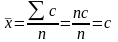
2. Средняя суммы (разности) двух или нескольких величин равна сумме (разности) их средних, т. е.

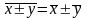
Доказательство:

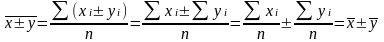
3. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты, т. е.

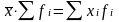
4. При уменьшении или увеличении вариант на одно и то же число, новая средняя изменится на то же число, т.е.

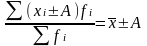
По примеру 2. Пусть А=12,5

Тогда

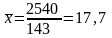
17,7 + А = 17,7 + 12,5 = 30,2

5. Если каждую варианту умножить или разделить на какое-либо произвольное число, то средняя арифметическая измениться во столько же раз, т. е. 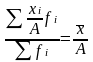и

Попробуйте проверить это свойство сами, аналогично предыдущему примеру.

6. Если все частоты разделить или умножить на какое-либо число, то средняя арифметическая от этого не измениться.

Доказательство:

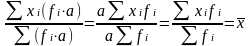
Следствие: при вычислении средней можно вместо абсолютных величин частот брать относительные величины в долях к единице или в процентах.

7. Сумма отклонений вариант от средней арифметической всегда равняется нулю, т.е. _.

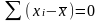Доказательство: 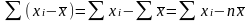из формулы средней арифметической простой: следует, что

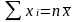
Таким образом, .

Логически это свойство значит, что в средней арифметической взаимно погашаются отклонения вариант в ту и другую сторону.

Расчет средней способом моментов нужен ли этот вопрос?

Изложенные выше свойства средней арифметической позволяют во многих случаях упростить ее расчеты с помощью так называемого «способа моментов».

Алгоритм расчета средней способом моментов:

1. Вычтем из всех вариант постоянное число (лучшее значение серединной варианты или варианты с наибольшей частотой).

2. Разделим варианты на постоянное число, а именно на велечину интервала.

3. Частоты выразим в процентах.

Пример 3. Распределение рабочих по размеру заработной платы

Группа рабочих по размеру заработной платы (ден. ед.)	Среднее значение интервала (хi)	Число рабочих (fi)	хi fi
60-70	65	10	650
70-80	75	30	2250
80-90	85	50	4250
90-100	95	60	5700
100-110	105	145 (max)	15225
110-120	115	110	12650
120-130	125	80	10000
130-140	135	15	2025
ИТОГО:	-	500	52700

4. Рассчитаем среднюю обычным путем:

ден. ед.

5. Рассчитаем среднюю способом моментов:

Среднее значение интервала (хi)	(хi-105)/10 ; (уi)	fi в процентах к итогу (i)	yi* i
65	- 4	2	- 8
75	- 3	6	- 18
85	- 2	10	- 20
95	- 1	12	- 12
105	0	29	0
115	1	22	22
125	2	16	32
135	3	3	9
ИТОГО:	-	100	5

Среднюю арифметическую из этих новых вариант называют моментом первого порядка (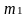 ), и выражают формулой:

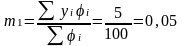
Что бы определить величину средней арифметической, нужно величину момента первого порядка умножить на величину того интервала, на который делили все варианты (в нашем примере 10), и прибавить к полученному произведению величину варианты, которую вычитали (105). Это можно записать так:

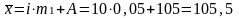ден. ед.