3. Мкэ для уравнения Пуассона

Уравнение Пуассона — эллиптическое дифференциальное уравнение в частных производных, которое описывает:электростатическое поле, стационарное поле температуры, поле давления, поле потенциала скорости в гидродинамике.

Оно названо в честь знаменитого французского физика и математика Симеона Дени Пуассона.

Это уравнение имеет вид:

{\displaystyle \Delta \varphi =f,}Где {\displaystyle \Delta } — оператор Лапласа, или лапласиан, а {\displaystyle f} вещественная или комплексная функция на некотором многообразии.

{\displaystyle \Delta \varphi =0.}Уравнение Пуассона может быть решено с использованием функции Грина; см., например, статью экранированное уравнение Пуассона. Есть различные методы для получения численных решений. Например, используется итерационный алгоритм — «релаксационный метод».

Уравнение Пуассона (неоднородное уравнение Лапласа). Δ = fU (1) Область применения данного уравнения – задачи электростатики, электронной оптики, теории упругости и др.

В данной статье мне хотелось бы изложить реализацию метода конечных элементов на примере уравнения Пуассона. Рассмотрим задачу:

(2)

с однородным краевым условием

(3)

где 

(4)

(5)

(6)

Требуется найти функцию  , решающую заданное уравнение.  3.1 Решение Умножим начальное уравнение на функцию  , непрерывную, кусочно непрерывно-дифференцируемую и равную на краях нулю, и проинтегрируем полученное уравнение по всей области  .  После применения формулы интегрирования по частям, получим следующее уравнение

(7)

Введем на области   квадратную сетку с шагом  :

(8)

и каждый квадрат разделим диагональю, параллельной биссектрисе первого координатного угла: 

Рисунок 1

Получим разбиение области   на треугольные элементы   — триангуляция области  . Триангуляция такого типа называется триангуляцией Фридрихса-Келлера.  Будем искать приближенное решение данного уравнения как функцию  , равную нулю на границе (краевое условие), непрерывную на области   и линейную на каждом полученном элементе триангуляции.  Функцию   можно представить в следующем виде: 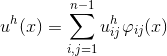(9)

где значения функций в точке   определены следующим образом:

(10)

(11)

Подставив функцию   в первое уравнение, осуществив преобразования и вынос констант изпод знака интеграла, сведем задачу для каждой базисной функции к подсчету интегралов вида: 

(12)

Значение интеграла может быть не нулевым лишь в том случае, если базисные функции под знаком интеграла имеют непустую общую область определения. По построению, каждый элемент имеет три вершины. Вершина может быть общей максимально для 6 треугольников: 

Рисунок 2

С соответствующими значениями производных для каждого из 6 случаев приведенных в таблице 1:

таблица 1

После подсчетов интеграла уравнение с номером   будет выглядеть следующим образом: (13)

где 

(14)

и при достаточно малом  : (15)

Следовательно, уравнение может быть переписано в следующем виде: (16)

Добавив граничные условия, а именно:

(17)

(18)

получаем полную СЛАР, решая которую, находим значения функции в точках сетки.

Выводы

Большая часть всех уравнений в частных производных 2^го порядка, линейных относительно вторых производных являются представителями 3^х различных классов уравнений, которые существенно отличаются друг от друга по методам исследования и по физической природе (описывают различные физические явления).

Любой процесс нагрева и охлаждения можно разделить на три стадии. Первая охватывает начало процесса и характеризуется постепенным распространением температурных возмущений, захватывающих все новые и новые участки материала.

Скорость изменения температуры в отдельных точках материала может быть различной и сильно зависит от начального распределения температур в теле и удаленности этих точек от источника нагрева или охлаждения.

Поэтому первая стадия процесса называется неупорядоченным режимом. С течением времени влияние начальных неравномерностей сглаживается, и относительная скорость изменения температуры во всех точках тела становится постоянной.

Наступает вторая стадия – режим упорядоченного процесса, который называют регулярным режимом.