6.2. Моменты инерции сечений простой формы

О пределим осевые моменты инерции прямоугольного сечения относительно центральных осей, параллельных его сторонам (рис. 6.4). Выбирая элементарную площадку в виде , получим:

(м⁴).

Аналогично

(м⁴).

Таким образом,

Рис. 6.4

^(6.9)

Так как z, y – оси симметрии, центробежный момент инерции

П олярный и осевые моменты инерции сечения в форме круга относительно полюса О и центральных осей z, y (рис. 6.5) находятся согласно следующим соотношениям:

;

(м⁴)

(или );

;

^{. (6.10)}

Определим момент инерции треугольного сечения относительно оси, параллельной осно­ванию (рис. 6.6).

Выбираем элементарную пло­щадку в виде полоски с раз­ме­рами (рис. 6.6).

Тогда .

У

Рис. 6.6

читывая, что , получим:

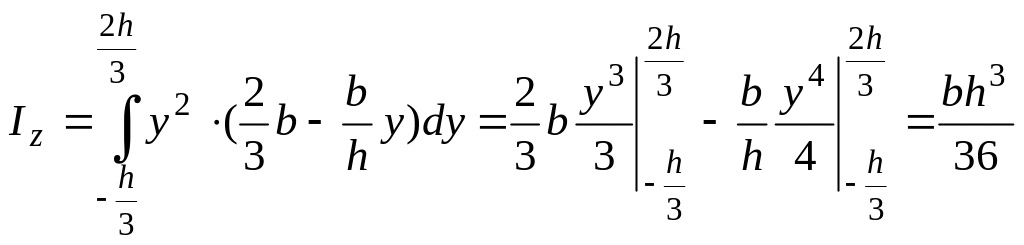. (6.11)

6.3. Формулы перехода при параллельном переносе и повороте осей

В том случае, когда сечение состоит из ряда простых фигур, моменты инерции которых относительно каких-либо осей (чаще всего – центральных осей самих фигур) известны, для определения моментов инерции относительно общих осей сечения удобно использовать формулы перехода. Преобразование плоской системы координат состоит из двух операций: параллельный перенос осей; поворот осей. Рассмотрим последовательно эти операции с позиции определения моментов инерции сечения в новой системе координат.

6.3.1. Параллельный перенос осей

Пусть моменты инерции , , сечения, показанного на рис. 6.7, известны и требуется определить моменты инерции сечения относительно осей z₁, y₁, параллельным осям z, y. Расстояния между осями z, z₁ и y,y₁ равны соответственно a, b. Координаты элементарной площадки dA в новой системе координат равны

(а)

Записывая интегральные выражения для осевых и центробежного моментов инерции сечения в новой системе координат , с учетом (а) получим:

;

_;

. (б)

Поскольку , , ,

, , , (в)

то, согласно (б), (в), получим окончательно формулы перехода для моментов инерции при параллельном переносе осей:

;

; (6.12)

.

Если оси – центральные, то . Следовательно, при переходе от центральных осей фигуры к нецентральным формулы (6.12) принимают вид:

;

; (6.12’)

.

6.3.2. Поворот осей

Пусть, как и ранее, известны моменты инерции , , сечения, показанного на рис. 6.8. Требуется определить моменты инерции относительно осей , повернутых относительно заданных осей на угол .

Используя геометрические построения (рис. 6.8), нетрудно получить следующие зависимости:

;

Рис. 6.8

. (г)

Так как , ,

, , (д)

то, подставляя (д) в (г), получим формулы преобразования координат элементарной площадки dA при повороте осей:

; . (е)

С учетом (е) интегральные выражения для моментов инерции сечения в новой системе координат принимают вид:

; (6.13)

; (6.14)

. (6.15)

Полученные выражения (6.13), (6.14), (6.15) представляют собой формулы перехода для моментов инерции сечения при повороте осей.

Учитывая, что , , , после преобразований получаем другой вариант формул перехода при повороте осей:

. (6.16)

. (6.17)

. (6.18)