16. Вычисления тройного интеграла.

Формулы вычисления тройного интеграла	Пример
Пусть областью интегрирования V является тело, ограниченное снизу поверхностью z=z1(х,у), сверху - поверхностью z=z2(х,у), причем z1(х,у) и z2(х,у) - непрерывные функции в замкнутой области D, являющейся проекцией тела на плоскость OXY. Тогда область V - правильная в направлении оси OZ. В декартовых координатах В цилиндрических координатах В сферических координатах

17. Числовые ряды. Основные понятия

Рассмотрим последовательность {An}; n=1, 2,…,…. Составим формально сумму A1+A2+A3+…=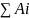 (1)

Сумма вида (1) наз-ся числовым рядом. Ai; i=1,2,3… наз-ся членами ряда

An – общий член ряда. An=F(n)

Ряд (1) задан, если задана функция, определенный общий член ряда, т.е An=F(n)

18. Необходимый признак СХ рядов. Достаточный признак РСХ рядов.

Теорема. Пусть ряд 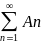(1) СХ, тогда общий член ряда стремится к нулю, т.е

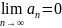
Док-во. Рассмотрим Sn=a1+a2+a3…+An. 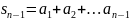=> 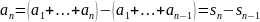(2)

По условию (1) СХ => ,

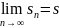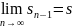
Из (2) => чтд

Следствие. Если 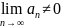, то ряд РСХ (Достаточный признак РСХ рядов)

19.Первый признак сравнения рядов.

Даны ряды:∑𝑎𝑛∞𝑛=1(1) и ∑𝑏𝑛∞𝑛=1(2)

Пусть an≤bn начиная с некоторого номера. Тогда из сх-ми ряда (2) =>сх-ть ряда(1)

Из расх-ти (1)=> расх-ть (2)

20. Второй признак сравнения рядов.

Даны ряды:∑𝑎𝑛∞𝑛=1(1) и ∑𝑏𝑛∞𝑛=1(2)

Пусть lim𝑛−∞𝑎𝑛𝑏𝑛 =k≠0-const

Тогда ряды 1 и 2 одновременно сходятся и расходятся

21. Признак Даламбера

Пусть дан ряд , и

Тогда: (1) сх при Д < 1

(1)расх при Д > 1

При Д=1 требуется дополнительное исследование.

Рекомендуется применять, когда общий член ряда содержит показатель функции или факториал

22. Признак Коши

Пусть дан ряд (1) и

Тогда: (1) сх при K < 1

(1)расх при К > 1

При К=1 требует дополнительного исследования.

23. Знакочередующийся ряд. Абсолютная и условная сходимость

Ряд называется знакочередующимся, если любые два соседних его члена имеют разные знаки, т.е. ряды вида u1 – u2 + u3 – u4 +… + un + …, где u1, u2, …, un, … положительны.

Ряд u1+u2+…+un+… называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные.

Знакочередующиеся ряды являются частным случаем знакопеременных рядов.

Абсолютная сходимость.

Теорема. Дан знакопеременный ряд u1+u2+…+un+…(1). Составим ряд |u1|+|u2|+…+|un|+… (2). Если ряд (2), составленный из абсолютных величин членов ряда (1), сходится, то ряд (1) сходится.

Определение. Знакопеременный ряд u1+u2+…+un+… называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов |u1|+|u2|+…+|un|+… .

Если же знакопеременный ряд (1) сходится, а ряд (2), составленный из абсолютных величин его членов, расходится, то данный знакопеременный ряд (1) называется условно или неабсолютно сходящимся рядом.

24. Признак Лейбница

Теорема Лейбница. Если члены знакочередующегося ряда, взятые по абсолютной величине, монотонно убывают и модуль общего члена ряда стремится к нулю при, то ряд сходится.