
- •1.Вильсон теоремасы
- •2. Симметриялы көпмүще туралы лемма.
- •3.Әртүрлі базистегі вектор координаталарының байланысы.
- •5. Группасының таблицасы жасау керек.
- •2)Антье функциясының қасиеттері
- •3)Вектор нормасы оның қасиеттері.
- •4)Алгебра ұғымы.Алгебра типі,мысалдар.Бір типті алгебралар.
- •1.Қалыңдылар кластарының толық системасы және оның қасиеттері.
- •2.Екі белгісізі бар екі теңдеу системасында белгісізді шығару.
- •3. Әр түрлі базистегі сызықтық оператор матрицаларының байланысы
- •4.Бинарлық қатынастардың берілу тәсілдері,бинарлық қатынасты граф арқылы беру,қатынас графиктері.
- •1.Модульмен өзара жай класстардың мультипликативті группасы, оның реті. Эйлер функциясының ұғымы. Мысал.
- •2. Кемел сандар. Жұп кемел сандар туралы теорема.
- •3.Евклидтік кеңістік ұғымы. Мысал. Стандартты евклид кеңістігі.
- •4. Бинарлық қатынастың негізгі қасиеттері және олардың графтағы көріністері.
- •6. Функциясы бойынша 252 мен 468 діңЕкое ін табу керек.
- •1.Қалындылар класының сақинасы.
- •2. Мебиус функциясы, қасиеттері.
- •3.Ортогональ базис құру(ортогональдау процесі).
- •4. Группа элементінің реті, оның қасиеттері.
- •1.Рефлексивті емес
- •1)Натурал сандардағы бөлу, бөлінді, бөлгіш, еселік ұғымдары. Функциялары.
- •2) Үздіксіз бөлшектер ұғымы, шектеулі, шексіз үздіксіз бөлшектер, мысал.
- •3) Берілген өрістегі векторлық кеңістік ұғымы. Мысалдары. Ішкі кеңістіктер.
- •4) Циклды группалар, ол туралы теорема.
- •1,Бүтін сандар жиынындағы салыстырулар қатынасы, мысал,анықтамадан шығатын қасиеттер,қалыңдылар қасиеті
- •5. Квадраттың айналулар жиының группасының таблицасын құр.
- •2. Лайықты бөлшектің алымы мен бөлімін анықтайтын формулалар
- •3. Векторлық кеңістіктің қасиеттері
- •1,Векторлық кеңістіктің анықтамасы.
- •1,Сызықтық кеңістіктің қарапайым қасиеттері
- •2,Бинарлық қатынас ұғымы. Екі жиынның тура көбейтіндісі. Мысалдар n-аралық қатынастар
- •2. Дәрежелік қосынды ұғымы. Оның қасиеттері туралы теорема.
- •3. Сызықтық оператор матрицасы. X пен ɸ(X) векторларының координат бағандарының байланысы.
- •4. Алгебралық операция ұғымы. N-арлық операциялар. Мысалдары
- •6. 91X ≡ 143 (mod 222) салыстыруды лайықты бөлшектер арқылы шешу керек.
- •18 Билет
3)Вектор нормасы оның қасиеттері.
Вектор-А бас нүктесінен бастап екінші В-соңғы нүктесіне дейінгі түзу бойындағы нүктелер жиыны, ал басқа жағдайларда әртүрлі векторлар-белгілі бір эквиваленттік қатынасы бойынша әртүрлі бағытталған кесінділерэквивалентті класстары болып табылады.
Х вектор нормасы ||х|| нөмірі болып табылады, егер 3 аксиоманы қанағаттандырса:
1)
||х|| 0,
мен ||х||
0,
мен ||х|| 0
сонда және тек қана сонда, x=0;
0
сонда және тек қана сонда, x=0;
2)
|| х||=||
|| ||х||
кез келген х вектор және кез келген
саны;
х||=||
|| ||х||
кез келген х вектор және кез келген
саны;
3) ||х+у||=||х||+||y||
Ең көп таралған 3 норма бар:
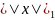 =
= ,
,
 =
1/2,
=
1/2,
 =
= .
.
Вектор нормасының қасиеттері:
1) ||A|| 0, мен ||A|| 0 сонда және тек қана сонда, A=0;
2) || A||=|| || ||A|| кез келген А матрицасы және кез келген саны;
3) ||А+В||=||А||+||В|| кез келген А және В матрицасы;
4)
||АВ|| ||А||||В||
||А||||В||
4)Алгебра ұғымы.Алгебра типі,мысалдар.Бір типті алгебралар.
Алгебра типі:
Сызықтық (немесе векторлық) кеңістікте әмбебап алгебраны бір бинарлық операциямен, унарлық операцияның қосындысы және жиыны арқылы, негізгі жазықтықтарға скаляр көбейтіндімен сипаттауға болады. Егер скалярдың орнына сақинаны алсақ, онда модульдың кең мағынасы шығады. Сызықтық кеңістікті, модульді,сонымен қатар сызықтық ауыстыруды зерттеуге байланысты сұрақтар алгебра бөлімінің-сызықтық алгебра бөлімінде қарастырылады.Алгебра бөліміне топологиялық алгебра, сонымен қатар топологиялық группаның теориясы және Ли группалары, нормаланған сақинаның теориясы, дифференциалдық алгебра, әртүрлі жинақталған алгебраны түрлері кіреді.
Бір типті алгебра:
А= және В=
және В=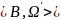 бір типті алгебраболатын В алгебрасы
алгебра бөлімі деп аталады, егер оған
А алгебрасы біртипті болса, егер В
А
және В-ның А-дағы бірдей көрсетілуі А
алгебрасындағы мономорфизмі болып
табылады.
бір типті алгебраболатын В алгебрасы
алгебра бөлімі деп аталады, егер оған
А алгебрасы біртипті болса, егер В
А
және В-ның А-дағы бірдей көрсетілуі А
алгебрасындағы мономорфизмі болып
табылады.
5) Квадрат емес тіктөртбұрыштың симметриялылығының группасының таблтцасы.


 4
3
4
3
I
1 2
3 2

 a
a
4 1
2 1
 a2
a2
3 4
 1
4
1
4
a3
2 3
1 2
b
4 3
4 3
ba
2
3 2
ba2
4 1
 2
1
2
1
ba3
3 4
|
І |
a |
a2 |
a3 |
b |
aa |
ba2 |
ba3 |
І |
І |
a |
a2 |
a3 |
b |
ba |
ba2 |
ba3 |
a |
a |
a2 |
a3 |
I |
ba3 |
b |
ba |
ba2 |
a2 |
a2 |
a3 |
I |
a |
ba2 |
ba3 |
b |
ba |
a3 |
a3 |
I |
a |
a2 |
ba |
ba2 |
ba3 |
B |
b |
b |
ba |
ba2 |
ba3 |
I |
a |
a2 |
a3 |
ba |
ba |
ba2 |
ba3 |
b |
a3 |
I |
a |
a2 |
ba2 |
ba2 |
ba3 |
b |
ba |
a2 |
a3 |
I |
A |
ba3 |
ba3 |
b |
ba |
ba2 |
a |
a2 |
a3 |
I |
6) 23 x3 15(mod 73)
23 x3 15 0(mod 73)
x x
x x
x x
x x
x x
x x
x x
x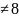 x
x x
x x
x x
x x=13
x=13
Жауабы: 13
17 билет
