4. Жиынтықтар параметрлерін бағалау
128~Статистикалық жиынтық – бұл:
|шексіз бірліктердің үлкен сандарынан тұратын элементтердің жиынтығы
|кез–келген зерттелетін құбылыстың жеке дербес жағдайы
|бақылау қамтылатын бас жиынтық элеметтерінің бөлігі
|бақылау элементтерінің жалпы саны
|уақытпен және кеңістікпен шектелген қандайда бір нысан белгісінің бірдей жиынтығы
129~Уақытпен және кеңістікпен шектелген қандайда бір нысан белгісінің бірдей жиынтығы ... деп аталады.
|бас жиынтық
|таңдамалы жиынтық
|статистикалық жиынтық
|жиынтық көлемі
|бақылаудың элементі
130~Статистикада бақылауға немесе өлшеуге болатын нысандардың немесе құбылыстардын қасиетін … деп аталады.
|көрсеткіш
|ерекшілік
|нәтиже
|белгі
|сипаттама
131~Егер тұтас бақылау жүргізу мүмкін болмаса, онда қолданылатын әдіс:
|таңдамалы
|жеке
|біркелкі
|бір қалыпты
|көрсеткіштік
132~Статистикалық жиынтықтағы белгілі бір шекті нысанды таңдап және оны зерттеудің статистикалық тексеру әдісі:
|жеке
|біркелкі
|бір қалыпты
|таңдамалы
|көрсеткіштік
133~Бас статистикалық жиынтық – бұл:
|зерттелетін құбылыстың кез келген дербес жағдайы
|бақылау бірлігін сипаттайтын белгі
|таңдау жүргізгенде алынған бас жиынтық элементтерінің бөлігі
|бақылау бірліктерінің жалпы саны
|шексіз бірліктердің үлкен сандарынан тұратын элементтердің жиынтығы
134~Шексіз бірліктердің үлкен сандарынан тұратын элементтердің жиынтығы ... деп аталады.
|статистикалық жиынтық
|бас жиынтық
|таңдамалы жиынтық
|жиынтық көлемі
|бақылаудың элементі
135~Таңдамалы жиынтық – бұл:
|шексіз бірліктердің үлкен сандарынан тұратын элементтердің жиынтығы
|зерттелетін құбылыстың кез келген дербес жағдайы
|бақылау бірлігін сипаттайтын белгі
|бақылау элеметтерінің жалпы саны
|бақылау қамтылатын бас жиынтық элеметтерінің бөлігі
136~Бақылау қамтылатын бас жиынтық элеметтерінің бөлігі алынған ... деп аталады.
|бас статистикалық жиынтық
|статистикалық жиынтық
|таңдамалы жиынтық
|тандама көлемі
|бақылаудың элементі
137~Таңдау көлемі – бұл:
|бақылау қамтылатын бас жиынтық элеметтерінің бөлігі
|шексіз бірліктердің үлкен сандарынан тұратын элементтердің жиынтығы
|зерттелетін құбылыстың кез–келген дербес жағдайы
|бақылау бірлігін сипаттайтын белгі
|бақылау элеметтерінің жалпы саны
138~Бақылау элементтерінің жалпы саны … деп аталады.
|таңдамалы жиынтық
|бас статистикалық жиынтық
|тандау көлемі
|статистикалық жиынтық
|бақылаудың элементі
139~Бақылаудың элементі – бұл:
|бақылау элементтерінің жалпы саны
|шексіз бірліктердің үлкен сандарынан тұратын элементтердің жиынтығы
|зерттелетін құбылыстың кез–келген дербес жағдайы
|бақылау қамтылатын бас жиынтық элеметтерінің бөлігі
|бақылау бірлігін сипаттайтын белгі
140~Кез–келген зерттелетін құбылыстың дербес жағдайы ... дап аталады.
|тандау көлемі
|таңдамалы жиынтық
|бақылаудың элементі
|бас статистикалық жиынтық
|статистикалық жиынтық
141~Аз таңдама көлемі:
|n≤50
|n≤60
|n≤30
|n≤100
|n≤200
142~Зерттеудің таңдамалы әдісінің негізі – бұл ... заңы.
|бір қалыпты үлестірім
|кеністіктің шексіздігі
|үлкен сандар
|Ньютон
|Пуассон
143~Үлкен сандар заңы ... сипаттайды.
|кездейсоқ шамалардың берілген сенімділікпен үлестірілуін
|бақылау саны артқан сайын жалпы кездейсоқ құбылыстарда кейбір орташалардың заңды тұрақтылығын
|бас жиынтық көрсеткіштердің арасындағы функционалдық тәуелділікті
|бас жиынтық көрсеткіштерінің арасындағы байланыстың тығыздығын
|бақылау саны артқан сайын таңдамалы жиынтықтың көрсеткіші бас жиынтыққа жақындау үрдісін
144~Таңдаудың негізгі қасиеті ... болып табылады.
|нұсқалық
|сенімділік
|үлгілік
|маңыздылық
|дәлдік
145~Бас жиынтықты сипаттамасына толықтай сәйкес келуі қасиеттің ... деп атайды.
|нұсқалық
|сенімділік
|үлгілік
|маңыздылық
|дәлдік
146~Таңдауды қалыптастыруға қойылатын негізгі талап ... болып табылады.
|таңдаудың бағыттылығы
|таңдаудың дәлдігі
|таңдаудың кездейсоқтығы
|дәл уақытында таңдау
|зерттеудің маңыздылығы
147~Сандық үлгілік – бұл:
|мүмкін болатын барлық бірлік бақылауды қамту
|зерттелетін белгілердің сандық қатынасы
|жеткілікті бақылау саны
|бас және таңдамалы жиынтықтың бақылау өлшем белгілерінің сәйкес келуі
|таңдамалы жиынтықтағы сандық белгілердің болуы
148~Сапалық үлгілік – бұл:
|таңдамалы жиынтықтың сапалы толық құндылығы
|мүмкін болатын барлық бірлік бақылауды қамту
|зерттелетін белгілердің сандық қатынасы
|бас және таңдамалы жиынтықтың бақылау өлшем белгілерінің сәйкес келуі
|таңдамалы жиынтықтағы сандық белгілердің болуы
149~Үлгілік таңдаманың түрі:
|толық, дербес
|кездейсоқ, анықталған
|сапалық, сандық
|дәл, анықталмаған
|тұтас, аралық
150~Вариацияланатын белгілердің мәні:
|жиіліктер
|нұсқалар
|децилер
|бөліктер
|квантилдер
151~Әрбір нұсқа қанша рет кездесетінін көрсететің санды ... деп атайды.
|нұсқалар
|жиіліктер
|децилер
|бөліктер
|квантилдер
152~Реттелген таңдама деп ... атайды.
|үлестірім заңын
|полигонды
|вариациялық қатарды
|гистограмманы
|нұсқаны
153~Вариациялық қатар ... түрінде ұсынылады.
|диаграма
|кесте
|шкала
|саны
|формула
154~Вариациялық қатарлардың түрі:
|сапалық, сандық
|дискретті, үздіксіз
|толық, дербес
|дәл, анықталмаған
|кездейсоқ, анықталған
155~ «xi», «νi» (xi – белгілердің нұсқасы, νi – жиілігі) нүктелерін қосатын сынық сызық түрінде ұсынылған сызба:
|гистограмма
|полигон
|радиалды диаграмма
|бағанаішілік диаграмма
|секторлық диаграмма
156~Суретте ұсынылған сызба:
|полигон
|гистограмма
|радиалды диаграмма
|бағанаішілік диаграмма
|секторлық диаграмма
157~ Стерджес формуласы ... санын анықтау үшін қолданылады.
|жиілік
|аралық
|бақылау
|белгі
|нұсқа
158~ Стерджес формуласы:
|k=1+3,322lgn
|k=1–3,322lgn
|k=2+3,322lgn
|k=2–3,322lgn
|k=3+3,322lgn
159~ Аралықтың шамасы ... формуласымен анықталады.
|
|
|
|
|
160~Суретте ұсынылған сызба:
|радиалдық диаграмма
|гистограмма
|бағанаішілік диаграмма
|секторлық диаграмма
|полигон
161~Аралық вариациялық қатарды гистограмма деп аталатын сатылы тұрпат түрдегі сызбамен көрсетуге болады:
|полигон
|радиадық диаграмма
|гистограмма
|секторлық диаграмма
|сызықтық диаграмма
162~Вариациялық қатар ... көрсеткіштерімен сипатталады.
|дискретті және үздіксіз
|толық және дербес
|орталық үрдіс және әр түрлілік
|кездейсоқ және анықталған
|сапалық және сандық
163~Орталық үрдіс көрсеткіштері:
|орташа және құрылымды шамалар
|абсолютті және салыстырмалы шамалар
|қарапайым және өлшенген шамалар
|полигон және гистограмма
|нұсқалар және жиіліктер
164~Қарапайым орташа арифметикалық шама формуласы:
|
|
|
|
|
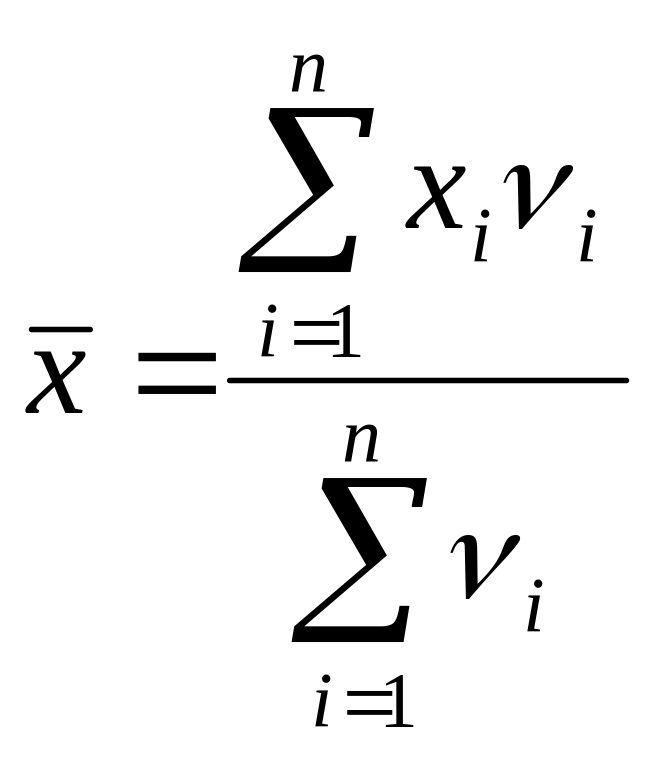
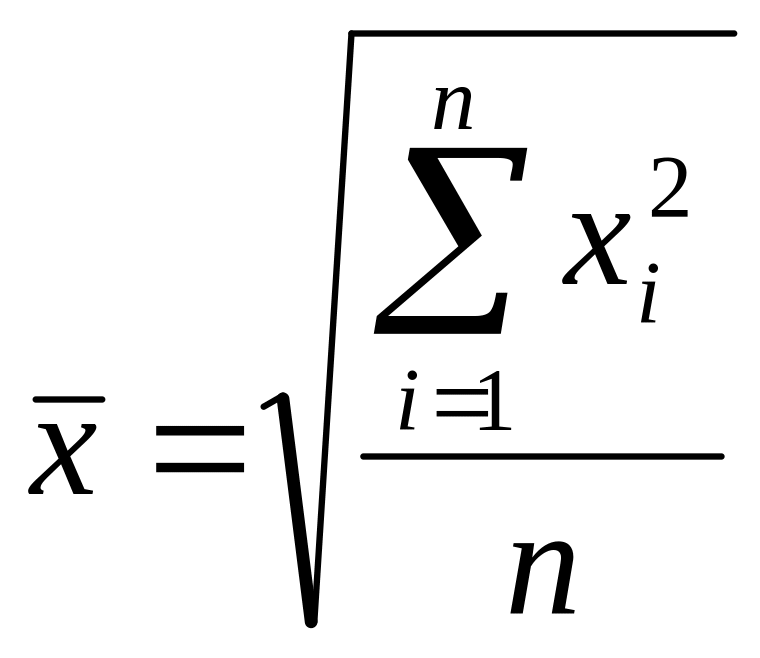
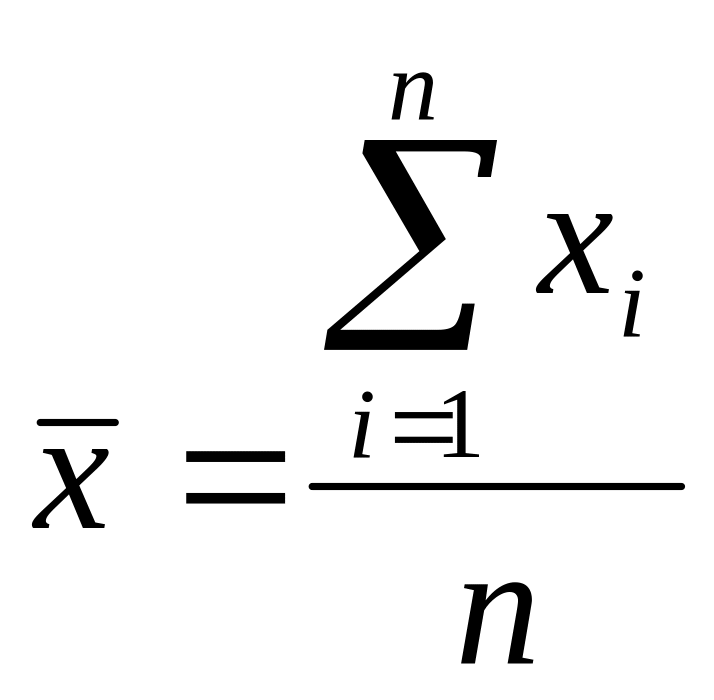
165~ – орташа… шама.
|арифметикалық қарапайым
|арифметикалық өлшенген
|геометриялық қарапайым
|квадраттық қарапайым
|өлшенген орташа квадраттық
166~Өлшенген орташа арифметикалық шама формуласы:
|
|
|
|
|
167~ – орташа ... шама.
|арифметикалық қарапайым
|геометриялық қарапайым
|арифметикалық өлшенген
|квадраттық қарапайым
|квадраттық өлшенген
168~Қарапайым орташа геометриялық шама формуласы:
|
|
|
|
|
169~ – орташа ... шама.
|арифметикалық қарапайым
|арифметикалық өлшенген
|геометриялық қарапайым
|квадраттық қарапайым
|квадраттық өлшенген
170~ Орташа квадраттық қарапайым шама формуласы:
|
|
|
|
|
171~ – орташа ... шама
| геометриялық қарапайым орташа
| квадраттық қарапайым
| арифметикалық қарапайым
|рифметикалықөлшенген
| квадраттық өлшенген
172~ Орташа квадраттық өлшенген шама формуласы:
|
|
|
|
|
173~ – орташа ... шама
|квадраттық қарапайым
|геометриялы қарапайым
|квадраттық өлшенген
|арифметикалықарапайым
|арифметикалық өлшенген
174~Қатар ортасында орналасқан нұсқа:
|мода
|дисперсия
|медиана
|орташа квадраттық ауытқу
|орташа арифметикалық шама
175~Медиана – бұл ... нұсқа.
|ең үлкен жиіліктегі
|ең кіші жиіліктегі
|қатар ортасында орналасқан
|қатар басында орналасқан
|қатар соңында орналасқан
176~Мода – бұл ... нұсқа.
|ең үлкен жиіліктегі
|ең кіші жиіліктегі
|қатар ортасында орналасқан
|қатар басында орналасқан
|қатар соңында орналасқан
177~Ең үлкен жиіліктегі нұсқа:
|медиана
|дисперсия
|мода
|орташа квадраттық ауытқу
|орташа арифметикалық шама
178~Вариациялық қатарды теңдей жеке бөліктерге бөлетін шама:
|квартилдер
|квинтилдер
|квантилдер
|децилдер
|процентилдер
179~Вариациялық қатарды теңдей төрт бөлікке бөлетін шама:
|квантилдер
|квартилдер
|децилдер
|процентлдер
|квинтилдер
180~Вариациялық қатарды теңдей бес бөлікке бөлетін шама:
|квартилдер
|квинтилдер
|квантилдер
|децилдер
|процентилдер
181~Вариациялық қатарды теңдей он бөлікке бөлетін шама:
|квартилдер
|квантилдер
|процентилдер
|децилдер
|квинтилдер
182~Вариациялық қатарды теңдей жүз бөлікке бөлетін шама:
|квинтилдер
|квартилдер
|квантилдер
|процентилдер
|децилдер
183~Процентилдер – бұл вариациялық қатарды теңдей ... бөлетін шама.
|бес бөлікке
|жүз бөлікке
|төрт бөлікке
|он бөлікке
|бөліктерге
184~Квартилдер – бұл вариациялық қатарды теңдей ... бөлетін шама.
|төрт бөлікке
|жүз бөлікке
|бес бөлікке
|он бөлікке
|бөліктерге
185~Децилдер – бұл вариациялық қатарды теңдей ... бөлетін шама.
|төрт бөлікке
|он бөлікке
|жүз бөлікке
|бес бөлікке
|бөліктерге
186~Квинтилдер – бұл вариациялық қатарды теңдей ... бөлетін шама.
|он бөлікке
|бес бөлікке
|төрт бөлікке
|жүз бөлікке
|бөліктерге
187~Квантилдер – бұл вариациялық қатарды теңдей ... бөлетін шама.
|бөліктерге
|бес бөлікке
|он бөлікке
|төрт бөлікке
|жүз бөлікке
188~Төменгі квартиль – бұл … процентиль.
|50–ші
|25–ші
|75–ші
|10–ші
|99–ші
189~Жоғары квартиль – бұл … процентиль.
|25–ші
|75–ші
|50–ші
|10–ші
|99–ші
190~Төменгі квартилдің нөмірі:
|
|
|
|
|
191~Жоғары квартилдің нөмірі:
|
|
|
|
|
192~Кездейсоқ шаманың оның орташа мәнінен шашырау шарасы:
|мода
|дисперсия
|медиана
|орташа квадраттық ауытқу
|таңдамалы орташа
193~Дисперсия – бұл:
|кездейсоқ шаманың нұсқадағы өлшем берлігімен берілген, оның орташа мәнінен шашырау шарасы
|орташадан алынған квадраттық түбір
|орталық үрдіс көрсеткіштері
|белгілер арасындағы байланыстың тарлығы
|кездейсоқ шаманың оның орташа мәнінен шашырау шарасы
194~Орташа квадраттық ауытқу – бұл:
|дисперсиядан алынған квадраттық түбір
|кездейсоқ шаманың оның орташа мәнінен шашырау шарасы
|кездейсоқ шаманың нұсқадағы өлшем берлігімен берілген, оның орташа мәнінен шашырау шарасы
|орталық үрдіс көрсеткіштері
|белгілер арасындағы байланыстың тарлығы
195~ Дисперсиядан алынған квадраттық түбір – бұл:
|таңдамалы орташа
|орташа квадраттық ауытқу
|мода
|медиана
|құлаш
196~Белгінің ең үлкен және ең кіші мәндерінің арасындағы айырым – бұл:
|құлаш
|орташа квадраттық ауытқу
|дисперсия
|таңдамалы орташа
|медиана
197~Егер таңдама вариациялық қатар түрінде берілсе, онда дисперсия ... формуласымен анықталады.
|
|
|
|
|
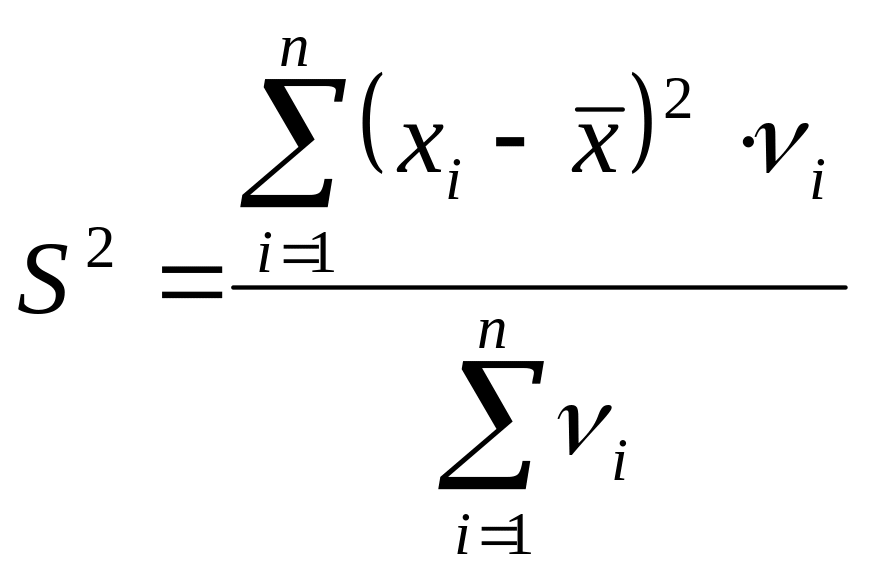
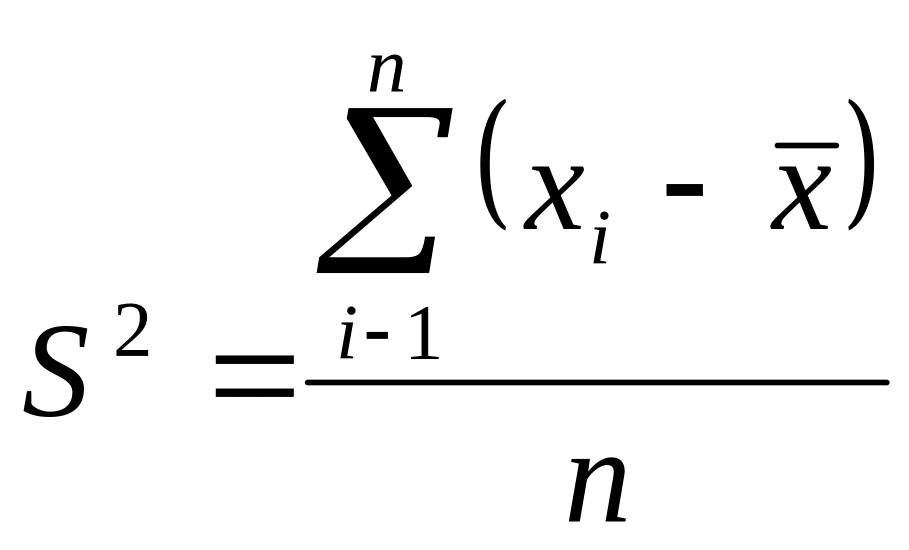
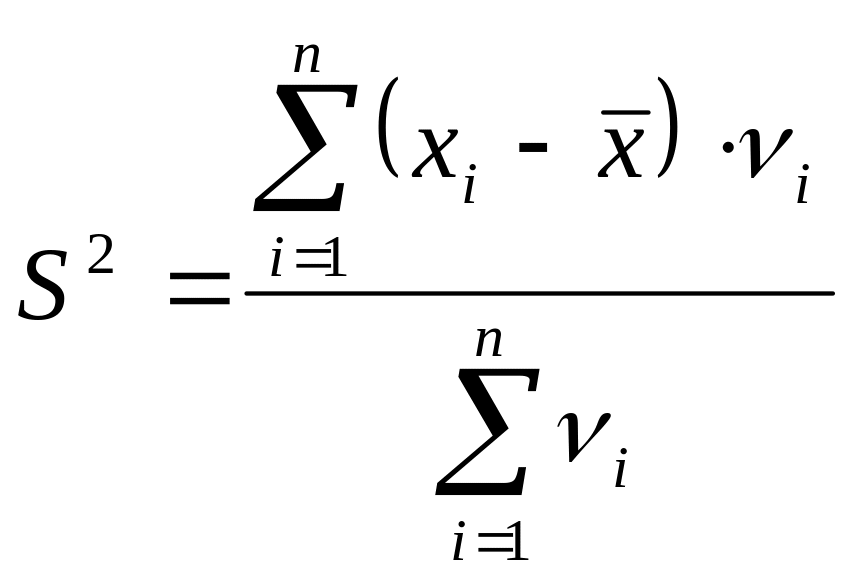
198~Егер таңдама кесте түрінде берілсе, онда дисперсия ... формуласымен анықталады.
|
|
|
|
|
199~ :
|таңдамалы орташа
|медиана
|таңдамалы дисперсия
|орташа квадраттық ауытқу
|құлаш
200~ :
|таңдамалы орташа
|таңдамалы дисперсия
|медиана
|орташа квадраттық ауытқу
|құлаш
201~
:
|орташа квадраттық ауытқу
|таңдамалы орташа
|таңдамалы дисперсия
|медиана
|құлаш
202~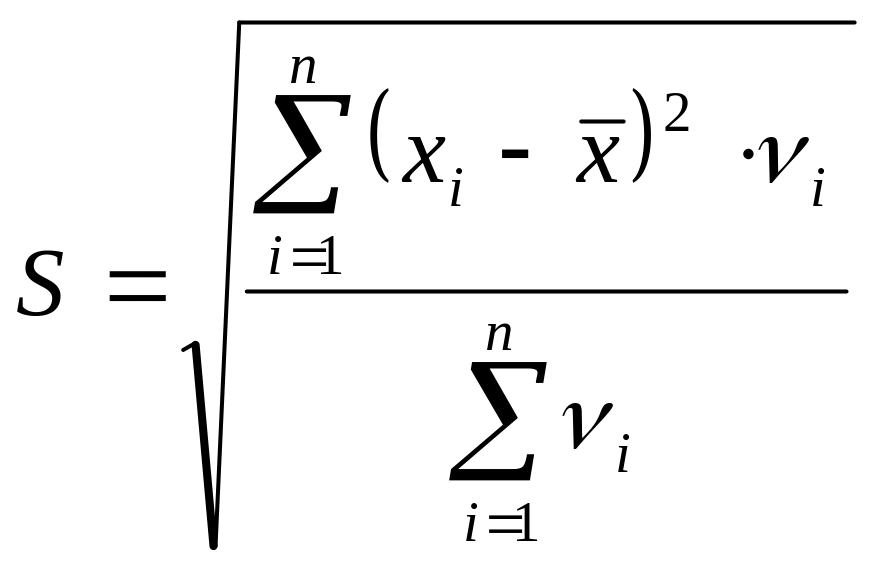
:
|таңдамалы орташа
|таңдамалы дисперсия
|медиана
|орташа квадраттық ауытқу
|құлаш
203~
:
|орташа квадраттық ауытқу
|құлаш
|таңдамалы орташа
|мода
|таңдамалы дисперсия
204~Кездейсоқ шаманың пайызбен берілген оның орташа мәнінен шашырау шарасы:
|дисперсия
|мода
|вариация коэффициенті
|таңдамалы орташа
|орташа квадраттық ауытқу
205~
:
|вариация коэффициенті
|дисперсия
|мода
|таңдамалы орташа
|орташа квадраттық ауытқу
206~Егер вариация коэффициенті ≤33% болса, онда таңдама:
|біртекті
|дәйекті
|ығысқан
|барабар
|анықталған
207~Егер вариация коэффициенті > 33% болса, онда таңдама:
|біртекті емес
|дәйекті емес
|ығыспаған
|барабар емес
|анықталмаған
208~Бас жиынтықтың сипаттамасы:
|параметрлер
|белгілер
|қасиеттер
|мәндер
|көрсеткіштер
209~Түзетілген таңдамалы дисперсия формуласы:
|
|
|
|
|
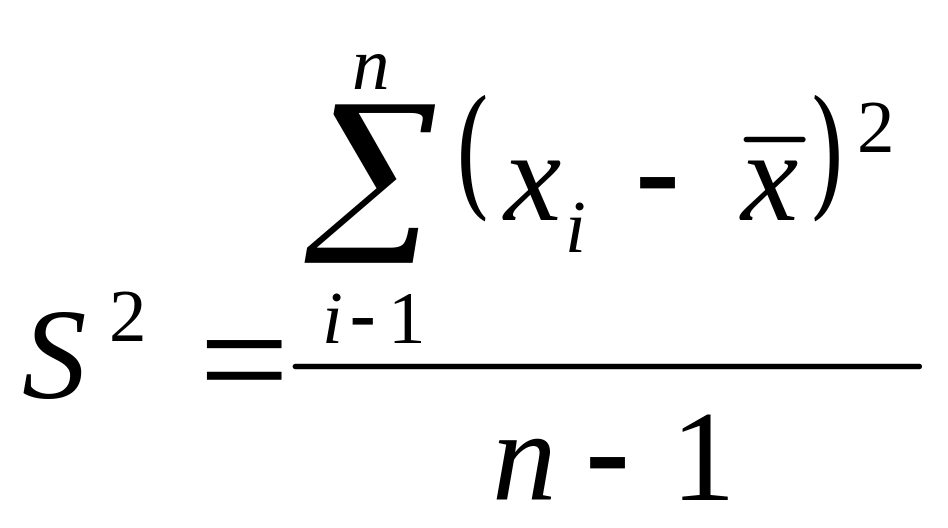
210~ :
|орташа квадраттық ауытқудың түзетілген таңдамасы
|түзетілген таңдамалы орташа
|таңдамалы дисперсия
|түзетілген таңдамалы дисперсия
|таңдамалы орташа квадраттық ауытқу
211~Орташа квадраттық қателік формуласы:
|
|
|
|
|
212~ :
|орташа квадраттық ауытқу
|орташа квадраттық қателік
|қалдық дисперсия
|таңдамалы дисперсия
|таңдамалы орташа
213~Кейбір жеке параметрлерді бағалауды ... бағалау береді.
|аралық
|нүктелік
|шектік
|сенімділік
|дәлдік
214~Параметрлерінің ... бағалауы деп «γ» ықтималдылығымен берілген параметрді екі жағынан жабатын нақты мәнінің аралығын айтады.
|нүктелік
|аралық
|шектік
|сенімділік
|дәлдік
215~Бас орташа үшін сенімділік аралығы:
|
|
|
|
|
216~ – бұл ... үшін сенімділік аралығы.
|бас дисперсия
|таңдамалы орташа
|бас орташа
|таңдамалы дисперсия
|түзетілген дисперсия
217~Оңтайлы таңдама көлемін есептейтін формула:
|
|
|
|
|
218~18 жастағы жас жігіттің орташа салмағы:
Салмағы хi, (кг) |
64 |
63 |
62 |
61 |
60 |
59 |
|
|
369 |
|
|||||
|60
|63,9
|61,5
|62
|59,3
219~18 жастағы жас жігіттің орташа салмағы:
Салмағы хi, (кг) |
64 |
63 |
62 |
61 |
60 |
59 |
|
Зерттеу саны νi |
2 |
3 |
9 |
6 |
4 |
1 |
|
|
1540 |
|
|||||
|
25 |
|
|||||
|50,1
|61,6
|69,8
|46,2
|55,6
220~Вариациялық қатардың модасы:
Салмағы хi, (кг) |
64 |
63 |
62 |
61 |
60 |
59 |
Зерттеу саны νi |
2 |
3 |
9 |
6 |
4 |
1 |
|63
|61
|62
|60
|64
221~Вариациялық қатардың медианасы:
Салмағы хi, (кг) |
64 |
63 |
62 |
61 |
60 |
59 |
Зерттеу саны νi |
2 |
3 |
9 |
6 |
4 |
1 |
|61,5
|63,5
|62,5
|60,5
|64,5
222~1–ден 2–ге дейін жастағы баланың басының орташа шеңбері:
Бастың шеңбері хi, (см) |
41 |
45 |
46 |
47 |
48 |
|
|
227 |
|
||||
|40,2
|45,4
|50
|42,7
|47,3
223~1–ден 2–ге дейін жастағы баланың басының орташа шеңбері:
Бастың шеңбері хi, (см) |
41 |
45 |
46 |
47 |
48 |
|
Зерттеу саны νi |
5 |
7 |
25 |
6 |
2 |
|
|
2048 |
|
||||
|
45 |
|
||||
|48
|60,3
|45,5
|40,9
|47,2
224~Вариациялық қатардың модасы:
Бастың шеңбері хi, (см) |
41 |
45 |
46 |
47 |
48 |
Зерттеу саны νi |
5 |
7 |
25 |
6 |
2 |
|41
|46
|45
|47
|48
225~Вариациялық қатардың медианасы:
Бастың шеңбері хi, (см) |
41 |
45 |
46 |
47 |
48 |
Зерттеу саны νi |
5 |
7 |
25 |
6 |
2 |
|41
|45
|46
|47
|48
226~Тамыр соғуының орташа жиілігі:
1 мин. жиілігі хi |
66 |
68 |
69 |
70 |
72 |
73 |
76 |
|
|
494 |
|
||||||
|70,6
|70
|68
|72,1
|76
227~Тамыр соғуының орташа жиілігі:
1 мин. жиілігі хi |
66 |
68 |
69 |
70 |
72 |
73 |
76 |
|
Зерттеу саны νi |
1 |
2 |
3 |
5 |
3 |
1 |
1 |
|
|
1124 |
|
||||||
|
16 |
|
||||||
|70,25
|70
|68,33
|70,2
|75
228~Вариациялық қатардың модасы:
1 мин. жиілігі хi |
66 |
68 |
69 |
70 |
72 |
73 |
76 |
Зерттеу саны νi |
1 |
2 |
3 |
5 |
3 |
1 |
1 |
|66
|70
|68
|69
|72
229~Вариациялық қатардың медианасы:
1 мин. жиілігі хi |
66 |
68 |
69 |
70 |
72 |
73 |
76 |
Зерттеу саны νi |
1 |
2 |
3 |
5 |
3 |
1 |
1 |
|66
|70
|68
|69
|72
230~Қандағы қанттың орташа мөлшері:
Қандағы қанттың мөлшері хi, (мг %) |
105 |
103 |
102 |
101 |
100 |
100 |
99 |
98 |
97 |
95 |
|
|
1000 |
|
|||||||||
|101
|100
|102
|99
|98
231~Қандағы қанттың орташа мөлшері:
Қандағы қанттың мөлшері хi, (мг %) |
105 |
103 |
102 |
101 |
100 |
99 |
98 |
97 |
95 |
|
Зерттеу саны νi |
1 |
1 |
2 |
3 |
7 |
3 |
1 |
1 |
1 |
|
|
2002 |
|
||||||||
|
20 |
|
||||||||
|102,3
|105,1
|100,1
|99,8
|95,2
232~Вариациялық қатардың медианасы:
Қандағы қанттың мөлшері хi, (мг %) |
105 |
103 |
102 |
101 |
100 |
99 |
98 |
97 |
95 |
Зерттеу саны νi |
1 |
1 |
2 |
3 |
7 |
3 |
1 |
1 |
1 |
|102
|100
|105
|99
|95
233~Вариациялық қатардың модасы:
Қандағы қанттың мөлшері хi, (мг %) |
105 |
103 |
102 |
101 |
100 |
99 |
98 |
97 |
95 |
Зерттеу саны νi |
1 |
1 |
2 |
3 |
7 |
3 |
1 |
1 |
1 |
|102
|105
|100
|99
|95
234~Вариациялық қатардың әр түрлілік көрсеткішіне ... жатпайды.
|дисперсия
|орташа квадраттық ауытқу
|мода
|ауытқу
|вариациялық коэффициенті