3. Бір қалыпты үлестірім және оның қасиеттері
88~
… үлестірім тығыздығы.
|бір қалыпты
|біркелкі
|көрсеткіштік
|биномиалды
|геометриялық
89~Біркелкі үлестірім тығыздығы:
|
|
|
|
|
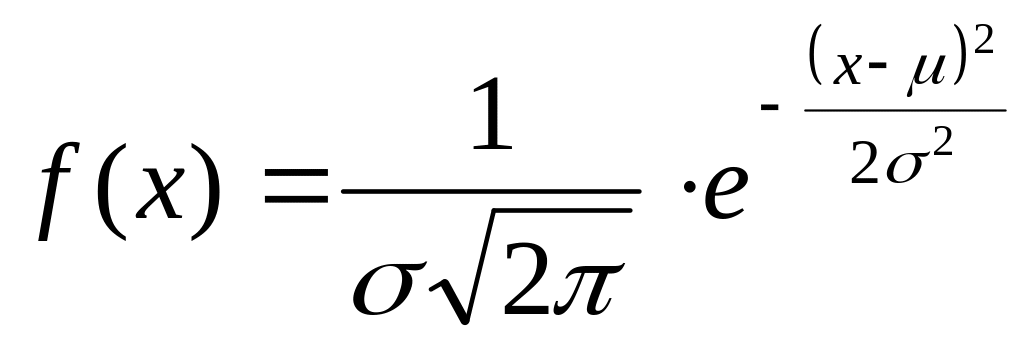
90~ … үлестірім тығыздығы.
|біркелкі
|бір қалыпты
|көрсеткіштік
|биномиалды
|геометриялық
91~Көрсеткіштік үлестірім тығыздығы:
|
|
|
|
|
92~ … үлестірім тығыздығы.
|көрсеткіштік
|біркелкі
|бір қалыпты
|биномиалды
|геометриялық
93~ Бір қалыпты үлестірім тығыздығы:
|
|
|
|
|
94~Сызбада көрсетілген кездейсоқ шамалардың үлестірімі:
|көрсеткіштік
|біркелкі
|бір қалыпты
|геометриялық
|биномиалды
95~Сызбада көрсетілген кездейсоқ шамалардың үлестірімі:
|біркелкі
|көрсеткіштік
|бір қалыпты
|геометриялық
|биномиалды
96~Сызбада көрсетілген кездейсоқ шамалардың үлестірімі:
|көрсеткіштік
|біркелкі
|бір қалыпты
|геометриялық
|биномиалды
97~ Бір қалыпты үлестірім заңы – бұл ... заңы.
|Пуассон
|Бернулли
|Гаусс
|Ляпунов
|Чебышев
98~Егер математикалық үміті µ=0 және орташа квадраттық ауытқуы σ=1 болса, онда бірқалыпты үлестірім ... деп аталады.
|нөлдік
|нормаланған
|симметриялы
|орташа
|бастапқы
99~Егер математикалық үміті µ=60 және орташа квадраттық ауытқуы σ=з болса, онда бір қалыпты үлестірімнің түрі:
|
|
|
|
|
100~Егер ықтималдықтың үлестірім тығыздық функциясының түрі болса, онда математикалық үміті ... тең болады.
|3–ке
|2–ге
|60–қа
|18–ге
|4–ке
101~Егер ықтималдықтың үлестірім тығыздық функциясының түрі болса, онда орташа квадраттық ауытқуы ... тең болады.
|60–қа
|3–ке
|2–ге
|18–ге
|4–ке
102~ Егер математикалық үміті µ=7,4 және орташа квадраттық ауытқуы σ=0,2 болса, онда ықтималдықтың үлестірім тығыздық функциясының түрі:
|
|
|
|
|
103~Егер ықтималдықтың үлестірім тығыздық функциясының түрі болса, онда математикалық үміті ... тең болады.
|7,4
|0,2
|2
|0,08
|4
104~Егер
ықтималдықтың үлестірім тығыздық
функциясының
түрі
болса, онда орташа квадраттық ауытқуы
... тең болады.
|0,2
|7,4
|2
|0,08
|4
105~Орташа мән өгергенде, бірқалыпты үлестірім тығыздығының сызбасы ... ығысады.
|вертикал өс бойымен жоғары немесе төмен
|горизонтал өс бойымен тек солға
|горизонтал өс бойымен оңға немесе солға
|горизонтал өс бойымен тек оңға
|вертикал өс бойымен тек жоғары
106~Орташа квадраттық ауытқу өгерген кезде, бірқалыпты үлестірім тығыздығы сызбасының ... өзгереді.
|ені
|биіктігі
|ұзындығы
|қалыңдығы
|ауданы
107~Егер кездейсоқ шама бір қалыпты үлестірілсе, онда бас жиынтықтың барлық мәндерінің 68,2%–ы ... аралығында жатады.
|
|
|
|
|
108~Егер кездейсоқ шама бір қалыпты үлестірілсе, онда бас жиынтықтың барлық мәндерінің 95,4%–ы ... аралығында жатады.
|
|
|
|
|
109~Егер кездейсоқ шама бір қалыпты үлестірілсе, онда бас жиынтықтың барлық мәндерінің 99,6% –ы ... аралығында жатады.
|
|
|
|
|
110~Егер кездейсоқ шама бір қалыпты үлестірілсе, онда аралығынды бас жиынтықтың барлық мәндерінің ... жатады.
|95,4%–ы
|68,2%–ы
|99,6%–ы
|55,5%–ы
|74,5%–ы
111~Егер кездейсоқ шама бір қалыпты үлестірілсе, онда аралығынды бас жиынтықтың барлық мәндерінің ... жатады.
|68,2%–ы
|95,4%–ы
|99,6%–ы
|55,5%–ы
|74,5%–ы
112~Егер кездейсоқ шама бір қалыпты үлестірілсе, онда аралығынды бас жиынтықтың барлық мәндерінің ... жатады.
|95,4%–ы
|68,2%–ы
|99,6%–ы
|55,5%–ы
|74,5%–ы
113~Медициналық–биологиялық зерттеулерде ... үлестірім жиі кездеседі.
|биноминалды
|бір қалыпты
|Пуассон
|біркелкі
|геометриялық
114~Биологиялық нысандарды үшін алғаш рет бір қалыпты үлестірімді қолданған ғалым:
|К. Пирсон
|А. Кетле
|Р. Фишер
|Ф. Гальтон
|В. Уэлдон
115~Бір қалыпты үлестірім параметрлерінің саны:
|1
|3
|2
|4
|5
116~Бір қалыпты үлестірім параметрлері:
|мода және медиана
|математикалық үміт және орташа квадраттық ауытқу
|мода және дисперсия
|математикалық үміт және вариация коэффициенті
|орташа квадраттық ауытқу және медиана
117~Симметриялы үлестірімнің «қисықтығының» сапалық шарасы – бұл ... коэффициенті.
|асимметрия
|бұзылу
|вариация
|детерминация
|корреляция
118~Асимметрия коэффициентінің формуласы:
|
|
|
|
|
119~ – бұл ... коэффициентінің формуласы.
|бұзылу
|вариация
|асимметрия
|детерминация
|корреляция
120~Егер асимметриия коэффициенті нөлден кіші болса, онда асимметрия:
|оңжақты
|біркелкі
|бір қалыпты
|солжақты
|көрсеткіштік
121~Егер асимметриия коэффициенті нөлден үлкен болса, онда асимметрия:
|біркелкі
|оңжақты
|бір қалыпты
|көрсеткіштік
|солжақты
122~Сызбада көрсетілген асимметрия:
|оңжақты
|солжақты
|біркелкі
|бір қалыпты
|көрсеткіштік
123~Сызбада көрсетілген асимметрия:
|солжақты
|біркелкі
|оңжақты
|бір қалыпты
|көрсеткіштік
124~Симметрия үлестірімнің «тіктілігінің» сандық шарасы – бұл ... коэффициенті.
|бұзылу
|асимметрия
|вариация
|детерминация
|корреляция
125~Эксцесс коэффициентінің формуласы:
|
|
|
|
|
126~ – бұл ... коэффициентінің формуласы.
|асимметрия
|вариация
|бұзылу
|детерминация
|корреляция
127~Егер бұзылу коэффициенті нөлге тең болса, онда үлестірілім:
|біркелкі
|бір қалыпты
|көрсеткіштік
|ассиметриялы
|бір қалыпты емес