
- •Дәріс сабақтардың тезистері
- •1 Тақырып. Термодинамикаға тарихи шолу. Классикалық статистика. Лиувиль теоремасы.
- •2 Тақырып. Термодинамикадағы энергияның рөлі.
- •4 Тақырып. Энтропия. Макроскопиялық қозғалыс.
- •5 Тақырып. Қысым, жұмыс және жылу мөлшері. Жылу функциясы. Еркін энергия.
- •6 Тақырып. Термодинамикалық потенциал (Гельмгольцтың энергиясы).
- •7 Тақырып. Термодинамикалық потенциалдың
- •8 Тақырып. Гиббстің функциясы. Гиббстің үлестіруі. Максвеллдің үлестіруі.
- •9 Тақырып. Идеал газдар. Тепе-теңсіздік күйдегі Больцманның идеал газдары.
- •Тақырып. Кванттық статистикадағы үлестірулер. Ферми-Дирак үлестіруі. Бозе-Эйнштейн үлестіруі.
- •12. Тақырып. Элементар бөлшектердің Ферми және Бозе газдары.
- •13 Тақырып. Сиретілген электронды газ. Қара сәулелену.
- •14 Тақырып. Конденсацияланған деңелер.
- •Энтропия.
- •2) Келесі теңдеуді табу үшін энтальпия: бұдан, ,
14 Тақырып. Конденсацияланған деңелер.
Қатты деңелер. Статистикалық әдістер қатты денелер үшін де қолданылады. Бұнда төменгі температурада атомдар аз тербелістер жасайды. Кристаллдық тор құрайды. Аморфтық да болады. Егер молекула саны N, ал молекуладағы атомдар саны ν болса, онда барлық атомдар Nν және 3Nν- тербелістердің еркіндік дәрежесінің саны.
Еркін энергия:
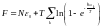 ,
мұндағы k=3Nν (1)
,
мұндағы k=3Nν (1)
Nε0-
молекулалардың өзара әсерлесу энергиясы,
ε0-
бір молекуланың энергиясы, N-
молекулалар саны
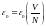 .
Қатты денелердің тербелістері қарапайым
дыбыс сияқты. Толқындар
.
Қатты денелердің тербелістері қарапайым
дыбыс сияқты. Толқындар
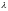 және
және
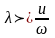 ,
мұндағы u-
дыбыс жылдамдығы, ω- жиілік,
,
мұндағы u-
дыбыс жылдамдығы, ω- жиілік,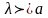 - тордың тұрақтысы.
- тордың тұрақтысы.
Қосындыдан интегралдауға жеңіл өтуге болады
 ,
,
мұнда
V-
дененің көлемі,
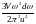 -
тербелістер саны.
-
тербелістер саны.
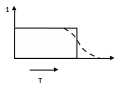 Интегралдан
келесі тендеу аламыз:
Интегралдан
келесі тендеу аламыз:
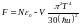 (2)
(2)
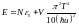 (F=1/3E=PV)
(F=1/3E=PV)
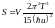
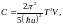 Cp=CV
–
төменгі температуралар үшін
Cp=CV
–
төменгі температуралар үшін
Және Т=0, S=0 (Нернст теоремасы).
Жоғары температурада
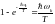 ,
онда
,
онда
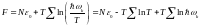
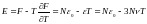 .
.
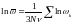 және
және
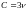 ,
онда
,
онда
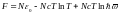
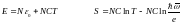 .
.
Көлем
үшін 3Nν:![]() .
.
Классикалық статистика үшін:

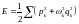 ,
,
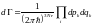
Әдебиеттер: негізгі және қосымша.
15 тақырып. Больцман және Боголюбов теңдеулері.
Больцманның кинетикалық теңдеуі.
Идеал газда бөлшектер өзра тек соқтығысулар кезінде әсерлеседі, соқтығысулар аралығында олар еркін және еріксіз болады. Газдың аз тығыздығы соқтығысуды екі-екіден деп есептеуге мүмкіндік береді. Бұл процессті идеал газға арналған кинетикалық теңдеумен сипаттауға болады.
Тепетеңсіз газ үшін таралу функциясы r, p және t-дан тәуелді. Фазалық кеністіктің элементі болса, онда t уақытында dγ мынаған тен болады:
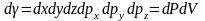
Сонда осы көлемде жатқан газ молекулаларының саны мынаған тең болады:
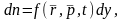
мұндағы
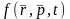 - таралу функциясы. Бұл көлемнен
молекулалар жаңа импульстарға ие бола
отырып кіреді немесе шығады, бұл процесс
соқтығысу нәтижесінде болады. Осылайша
көлемдегі бөлшектер саны өзгереді,
яғни
- таралу функциясы. Бұл көлемнен
молекулалар жаңа импульстарға ие бола
отырып кіреді немесе шығады, бұл процесс
соқтығысу нәтижесінде болады. Осылайша
көлемдегі бөлшектер саны өзгереді,
яғни
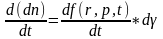 (1) немесе
(1) немесе 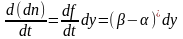 (2)
(2)
мұнда αdγ – көлемді тастап кететін бөлшектер саны, ал βdγ – көлемге кіретің бөлшектер саны. Сәйкесінше,
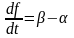 (3)
(3)
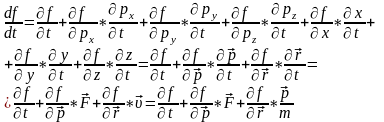
мұндағы
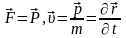
Демек,
 (4)
(4)
Бір жағынан αdγ және α-ны, сондай-ақ βdγ және β-ны табуға болады. өатан соқтығысулар теориясынан. Мысалы:
 (5)
(5)
немесе
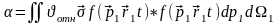 (6)
(6)
мұндағы
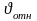 - салыстырмалы жылдамдық, σ1
–
шашырау қимасы, і – шашырау бұрышы, Ω1-
бірінші бөліктің денелік бұрышы, р1-
бөлшектің импульсі. Сондай-ақ βdγ және
β-ны табуға болады:
- салыстырмалы жылдамдық, σ1
–
шашырау қимасы, і – шашырау бұрышы, Ω1-
бірінші бөліктің денелік бұрышы, р1-
бөлшектің импульсі. Сондай-ақ βdγ және
β-ны табуға болады:
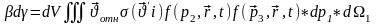 (7)
(7)
dр3dр2=dр1dр - Лиувиль теоремасы және
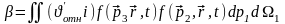 (8)
болғандықтан
(8)
болғандықтан
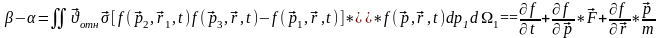
шығады. Бұл тендеу Больцманның тендеуі деп аталады.
Н.Н. Боголюбовтің кинетикалық теңдеуі.
Больцман теңдеуі қатан емес, - өйткені:
Сол жақ болігі тығыздықтар айрымынан немесе сыртқы өріс әсерінен үзіліссіздік теңдеуі болып табылады. Оң жақ болігі – соқтығысқа тәуелді. Және де олар осылайша басқаларына әсер етпейді.
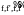 бір
бір
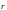 нұктесінде шексіз, молекулалар өлшемі
ескерілмейді. Молекулалар
жылдамдықтарының арасындағы корреляция
жоқ.
нұктесінде шексіз, молекулалар өлшемі
ескерілмейді. Молекулалар
жылдамдықтарының арасындағы корреляция
жоқ.
Басты өлшемсіз соқтығыстар тек жұп бөлшектердікі. Үлкен тығыздықтарда үш, төрт және т.с.с. бөлшектердің соқтығысы болуы мүмкін және т.б.
Боголюбов теңдеуі қатаңырақ болып табылады.
Қорытындыдан:
N бірдей бөлшект болсын. Үлестіріле
функциясы
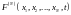 ,
ал ықтималдылық
,
ал ықтималдылық
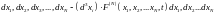 көлемде орналасқан нүктелермен
бейнеленеді және бірге нормаланады.
көлемде орналасқан нүктелермен
бейнеленеді және бірге нормаланады.
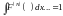 . (1)
. (1)
Сыртқы
өріс жоқ болсын, бөлшектер
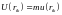 потенциалмен өзара әрекеттеседі делік.
Және де F(N)-
Лиувилль теңдеуіне жауап береді:
потенциалмен өзара әрекеттеседі делік.
Және де F(N)-
Лиувилль теңдеуіне жауап береді:
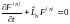 , (2)
, (2)
мұндағы
 . (3)
. (3)
Егер
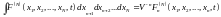 деп
жазсақ, (4)
деп
жазсақ, (4)
онда n - квазиклассикалық функция және статистиалық функция болып табылады. Осы кезде
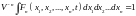 нормалау.
нормалау.
Ықшамдау
үшін (N)
индексін ескермейміз. Егер (2) теңдеуді
(3) теңдеуін есепке ала отырып,
 көбейтсек және интегралдап:
көбейтсек және интегралдап:
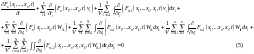 аламыз.
аламыз.
Бесінші интеграл мынаған тең:
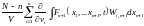 ,
,
онда (5) муше келесі түрде болады:
 (6)
(6)
Берілген теңдеу Боголюбов теңдеуі деп аталады.
Егер
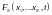 болса, онда (5) теңдеуі Лиувилль теңдеуіне
тең болады және де тұйықталған болып
табылады.
болса, онда (5) теңдеуі Лиувилль теңдеуіне
тең болады және де тұйықталған болып
табылады.
Мысалы, бір бөлшекті жүйе үшін F1(x1,t), екі бөлшекті үшін F1(x1,x2,t).
Осылар үшін:
 .
.

м![]() ұндағы
ұндағы
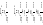 ;
F3=F3(x1,x2,x3,t).
;
F3=F3(x1,x2,x3,t).
Әдебиеттер: негізгі және қосымша.
Практикалық сабактардын жоспары
Практикалық сабактар лекцияда окытылған материалдардың мазмұнына сәйкес есеп шығару түрінде өткізіледі.
Есептер термодинамика және статистикалық физика курсы бойынша құрастырған есептер жинағынан алынады.
Физикалық есептерді шығару женіндегі нұсқаулар термодинамика және статистикалық физика бойынша шығарылған оқу-әдістемелік кешенде келтірілген.
Статистикалық физика және конденсірлі орталар физикасы курсы бойынша есептер шығарудың ерекшеліктері әр бір тарауда мысалдар түрінде келтірілген.
Тапсырма.
Оқытушының нұсқауымен өзінің жеке тапсырманы таңдаңыз. Тапсырманың шарты мен бастапқы берілгендерін, сонымен бірге нәтижелерді енгізу мен шығаруы кезіндегі түрлендірудің функциялары мен айнымалылар типтерін нақтылап алыңыз.
Орындауға әдістемелік нұсқаулар.
Оқу практикасында физикалық есеп деп, әдетте физиканың зандары мен әдістерінің негізінде, жалпы түрде логикалық ой
тұжырымның, математикалық әрекеттердің және эксперименттің көмегімен шешілетін кішігірім мәселені айтады.
Мәселеге тікелей байланысты қарастыратын болсақ, физика сабақтарында оқу материалын оқып үйренуге байланысты пайда болған әрбір сұрақ, оқушылар үшін есеп болып табылады.
Әдістемелік және оқулық әдебиетте есепті, әдетте, басты міндеті оқушылардың физикалық құбылыстарды оқып үйрену, түсініктерді қалыптастыру, физикалық ойын дамыту және білімдерін практикада қолдана алуды дағдыландыру болатын, мақсатқа сәйкес іріктеліп алынған жаттығулар деп түсінеді. Есептерді шығару көптеген басқада мақсаттарды, мысалы, білім, біліктілік және дағдыны бақьыау және есепке алуды көздейді.
Физика есептері көптеген белгілермен топтастырылады: мазмұны бойынша, шешу тәсілі бойынша, қиындық дәрежесі бойынша.
Мазмұны бойынша дерексіз (абстрактылы) және нақты есептер, өндірістік және тарихи мазмұнды есептер, сонымен қатар кызықты есептер деп ажыратылады.
Шешу тәсілі бойынша сапалык (оқулық), эксперименттік, есептік және графиктік есептер деп ажыратылады. Бұл бөліну шартты болып табылады, өйткені есептердің көпшілігін шешуде бірнеше тәсіл қолданылады. Мысалы, эксперименттік есепті шешуде ауызша ойлау, сонымен бірге көптеген жағдайларда есептеу және графикпен жүмыс қажет.
Мазмұны бойынша күрделі емес есептер, мысалға формула мағынасын ашуды, өлшем бірліктер жүйесін іріктеуді, қандай да шаманы дайын формула бойынша табуды және т.с.с. талап ететін, тақырыпты оқып үйрену процесіде шығарылады.
Күрделі есептер проблемалық жағдайлардан және жаңалық элементтерінен түрады. Осындай есептерге физика сабақтарында басты назар аударады. Оларды шығаруға арнайы уақыт бөлінеді, сонымен қатар жеке есеп шығару сабактары.
Келтірілген есеп типтерінің арасында ерекше шек жоқ. Есепті бірте-бірте қиындата отырып, тек проблема қойылған және "еш нәрсе берілмеген" есептерге келеді. Осындай есептерді жиі "шығармашылық" деп атайды. Кейбір әдіскерлер оларды екі негізгі түрге бөледі: "зерттеушілік" (неге? деген сүраққа жауапты талап ететін) және "конструкторлық" (қалай жасау керек? деген
сүраққа жауап талап ететін). Шығармашылық есептер сапалык, есептеу немесе эксперименттік болуы мүмкін.
Ерекше орынды күрделі қиындатылған, олимпиадалық деп аталатьш есептер алады.
Есептерді шығару әдістемесі көптеген шарттарға тәуелді: оның мазмүнына, оқушылардың дайындығына, оқытушының қойған мақсатына және т.с.с. Сонда да оқушылармен бірге есеп шығару барысында ескеретін, есептердің көпшілігіне тиісті жайлар бар:
Есепті шығару, ондағы берілгенді назар салып оқу және үғынудан басталады. Осы кезде жаңа терминдердің мәні,түсініксіз формулалар және т.б. анықталады.
Содан соң бір бағанаға есеп шартында кездесетін ретпен, берілгендер жазылады. Төменірек, "керек болған жағдайда",кестелік берілгендер үшін бірнеше қатар қалдырады.
Оң жағынан есептер жинағында болсада, сәйкесті сызба жасайды. Сызбаны қолданып әр түрлі жорамалдарға ерекше назар аудара отырып, есеп шартын талдайды. Жорамалдардың бірі есеп шартында айтылады, басқасын оқытушының қойған мақсатына қарай, оқушылардың дайындығына қарай есепті шешу барысында жасаған жөн.
Есептердің көпшілігін аналитико-синтетикалық әдіспен шығарады, бірақ осы кезде шығаруды "соңынан", яғни ізделініп отырған шама кіретін өрнекті талдаудан бастауға оқушыларды үйрету қажет.
Есептердің көпшілігін, әсіресе жоғары сыныптарда, жалпы түрде шығаруға тырысу керек, ал содан соң сандык есептеулер жүргізуге болады. Бүл уақытты үнемдейді, өйткені арасындағы сандық есептеулер керексіз болуы мүмкін, сонымен қатар шешімін тексеруді және оны талдауды женілдетеді.
Сандық есептеулер үшін (есеп шартында-ақ) берілгендерді бірдей өлшем бірліктермен, яғни СИ жүйесінде келтірген жөн.
7. Содан сон есептеулерді орындайды, осы кезде ізделінетін шаманың дәрежесін орнатады, егер нәтижені бағалау қиындық тудыратын болса, онда калькулятор қолданады. Сонымен қатар жуық сандармен жұмыс істеу ережелерін қолданған жөн.
Сабақ 1. Классикалық статистика. Лиувиль теоремасы.
Сұрақтар:
Термодинамика.
Гиббс, Больцман принциптері.
Термодинамиканығ ең негізгі ұғымдары.
Фазалық траектория, фазалық көлем.
Лиувильдің теңдеуі.
Тапсырма:
Семестрлік жұмысты орындауға байланысты теориялық сұрақтармен жұмыс.
Есепті шығару мысалы.

теңсіздігін дәлелдеңіз.
Шешімі:
Берілген есеп шартын мынадай анықтауыш
түрінде жазуға болатыны болады:

Якобиандар әдісін қодданып,
![]()
Бірақ
, мына теңдеуден
![]() келесі
теңсіздікті
келесі
теңсіздікті
аламыз:
![]() сондықтан,
бұл теңсіздік бірге тең.
сондықтан,
бұл теңсіздік бірге тең.
Әдебиеттер: [6] әдебиет бойынша есептер шығару.
Сабақ 2. Термодинамикадағы энергияның ролі, негізгі қозғалыс интегралдары.
Сұрақтар:
Термодинамикадағы энергияның ролі.
Лиувильдің теоремасы.
Сақталу заңдары.
Термодинамиканың аддитивті шамалар ы.
Тапсырма:
Семестрлік жұмысты орындауға байланысты теориялық сұрақтармен жұмыс.
Есепті шығару мысалы.
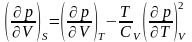 теңсіздікті
дәлелдеңіз.
теңсіздікті
дәлелдеңіз.
Шешімі: Жоғарғы есепке ұқсас Якобиандар әдісімен шығарамыз,
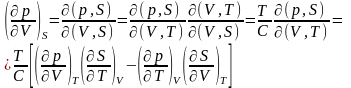
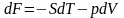 шартын
есепке ала отырып, берілген есеп
шартының шешіміне келеміз.
шартын
есепке ала отырып, берілген есеп
шартының шешіміне келеміз.
Әдебиеттер: [6] әдебиет бойынша есептер шығару.
Сабақ 3. Статистикалық матрица. Ықтималдық үлестіру.
Сұрақтар:
Статистикалық матрица.
Статистикалық матрица.
Шредингер теңдеуі.
Ықтималдық үлестіру.
Тапсырма:
1. Семестрлік жұмысты орындауға байланысты теориялық сұрақтармен жұмыс.
2. Есепті шығару мысалы.
р және S тәуелсіз айнымалы шамалар деп есептеп,
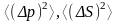 және
және
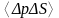 флуктуацияларды шешіңіз.
флуктуацияларды шешіңіз.
Шешімі:
р
және S тәуелсіз шамалардың флуктуациялары
аркылы![]() және
және![]() мәндерін
келесі түрде келтіреміз:
мәндерін
келесі түрде келтіреміз:
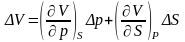 ,
,
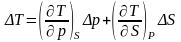 (1)
(1)
![]() қатынас
арқылы,
қатынас
арқылы,
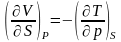
Одан
кейін: 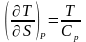
Сондықтан (1) - ші тендеу мына түрде көшіріледі:

Алынған тендеулерден
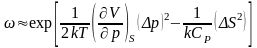 (2)
(2)
(2)-шіден
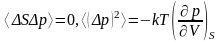
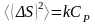
Сабақ 4. Энторпия. Макроскопиялық қозғалыс.
Сұрақтар:
