Вопрос №8:

Наудачу выбрано число, не превосходящее 19. Какова вероятность того, что это число делится на 4?

Решение (в условии под числом подразумевается натуральное число)

Используем классическое определение вероятности.

Общее число элементарных исходов равно 19.

Имеется ровно 4 натуральных числа меньших 19 и делящихся на 4, это числа: 4, 8, 12, 16. Значит благоприятных исходов 4.

Поэтому искомая вероятность равна

Вопрос №9:

Случайная величина Х задана дифференциальной функцией распределения 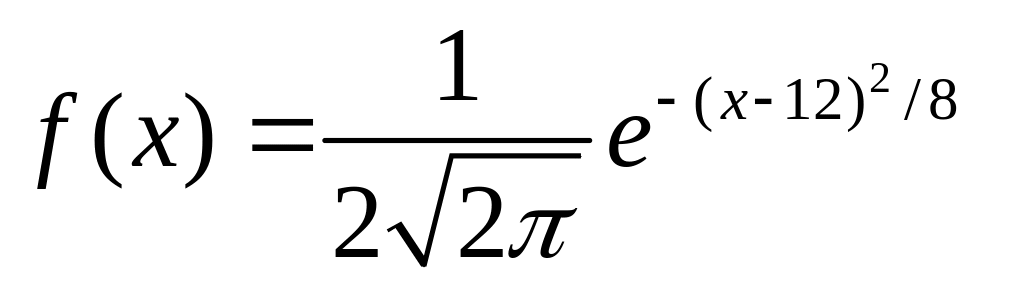. Найти М(3Х9)+D(3Х9) .

Решение

Рассматриваемая величина распределена по нормальному закону, для которого плотность вероятности (дифференциальная функция распределения) имеет вид: . Сравнив это выражение с выражением из условия задачи, определяем, что , .

Для нормально распределенной величины Х .

Далее используем свойства математического ожидания и дисперсии:

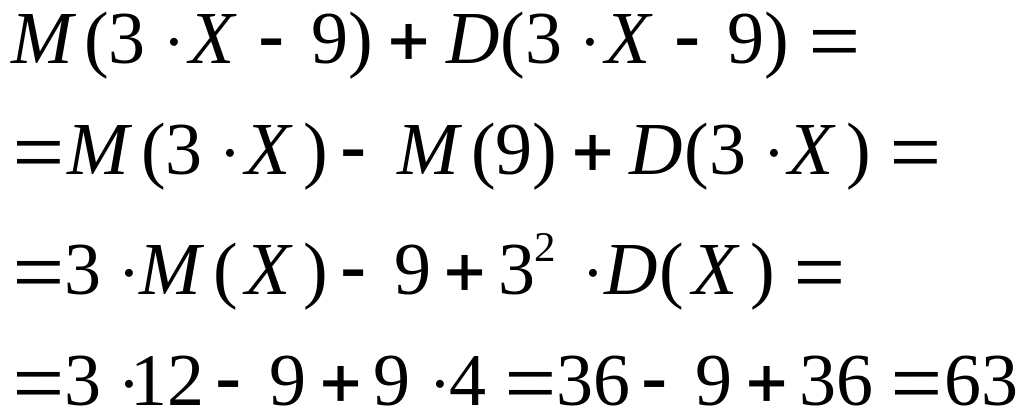
Замечание: при решении задачи использованы свойства (в общем виде):

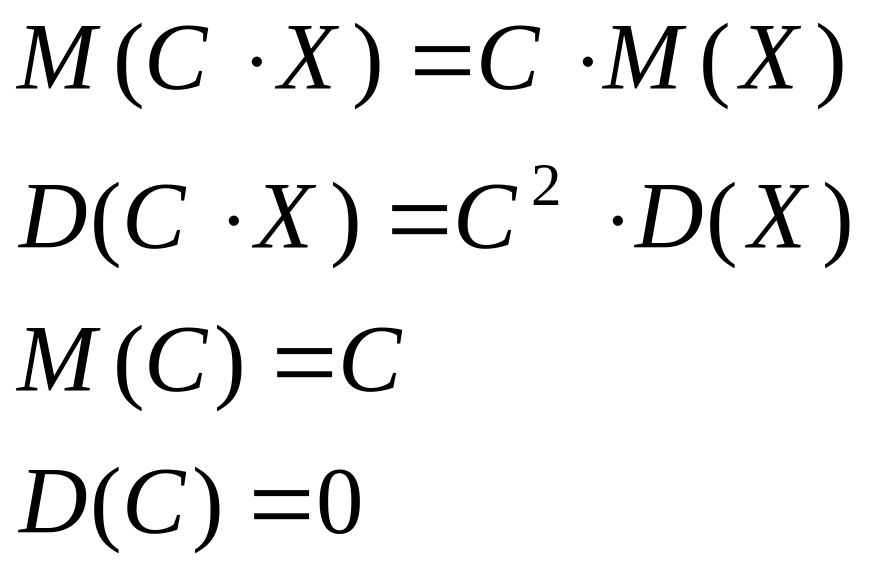
где С – число. Последние два свойства легко запомнить: математическое ожидание константы равно самой этой константе как ее среднее значение. Дисперсия константы равна нолю, т.к. дисперсия характеризует разброс значений относительно среднего, а разброс относительно постоянного числа отсутствует.

Вопрос №10:

Два баскетболиста делают по одному броску в корзину. Вероятность попадания для одного из них равна 0.8, а для другого 0.7.

а) Найти вероятность того, что ровно один из них промахнется.

б) Найти вероятность того, что хотя бы один из них промахнется.

в) Найти вероятность того, что хотя бы один из них попадет.

Решение

Обозначим буквой (событие) попадание первого баскетболиста, буквой (событие) попадание второго баскетболиста.

а) Нам нужно найти вероятность события .

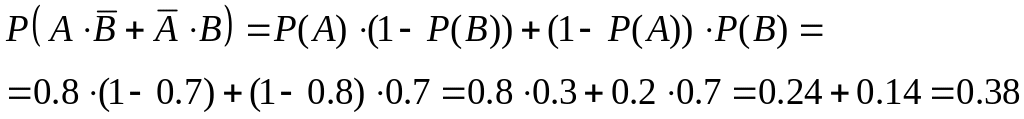
б) Нам нужно найти вероятность хотя бы одного промаха. Здесь удобнее найти сначала вероятность противоположного события – «оба попали»:

Тогда вероятность хотя бы одного промаха:

в) Нам нужно найти вероятность хотя бы одного попадания. Здесь удобнее найти сначала вероятность противоположного события – «оба промахнулись»:

Тогда вероятность хотя бы одного попадания:

Вопрос №11:

Опыт состоит в последовательном бросании двух монет. Рассматриваются события:

А - выпадение хотя бы одной цифры;

В - выпадение герба на второй монете.

Определить условную вероятность Р(В/А) - вероятность события В при условии, что событие А произошло.

Решение

Выпишем сначала все исходы (Г- герб Ц – цифра):

ГГ

ГЦ

ЦГ

ЦЦ

Событию А благоприятствуют 3 исхода: ГЦ, ЦГ, ЦЦ.

Событию АВ (хотя бы одна цифра и герб на второй монете) благоприятствует 1 исход: ЦГ.

Условная вероятность равна:

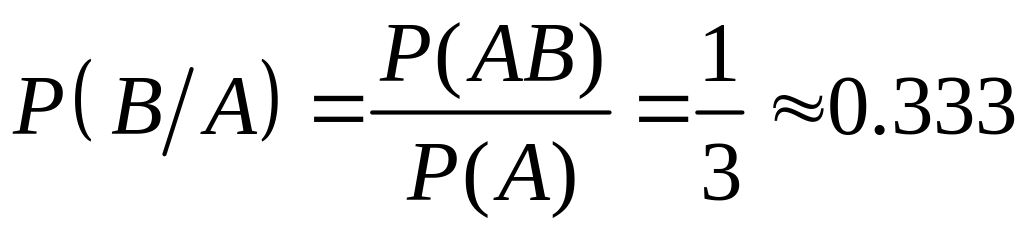
Вопрос №12:

При передаче сообщения вероятность искажения для каждого знака равна 0,1. Найти вероятность того, что сообщение из 5 знаков содержит ровно 3 искажения.

Решение

Для решения этой задачи нужно использовать формулу Бернулли:

В этой задаче , , , .

Итак:

При вычислении мы использовали свойство: .

Замечание: формула Бернулли применяется только тогда, когда проводится несколько испытаний, и вероятность события в каждом испытании ОДИНАКОВАЯ.