1.2. Минимизируемые термодинамические потенциалы
Чтобы корректно построить физико-химическую модель, необходимо четко определить независимые параметры состояния, поскольку именно они определяют условия равновесия системы. Природные и технологические объекты подчинены определенным термодинамическим условиям существования. Поэтому выделение в них независимых и зависимых параметров не является произвольным, а диктуется характером тех процессов, которые допускаются условиями существования гетерогенных систем.
Независимыми
факторами состояния большинства
высокотемпературных технологических
процессов являются давление и температура,
поэтому равновесие в них целесообразно
определять с помощью минимума
изобарно-изотермического потенциала
G (T,P) (свободной энергии Гиббса).
В
круглых скобках указаны независимые
факторы состояния систем: Т– температура,
Р– давление.Наиболее полно этим
требованиям удовлетворяет
изобарно-изотермический потенциал, с
помощью которого условие перехода
вещества А из фазового состояния
в
фазовое состояние
может
быть записано в виде:
G(A;
)=
G(A;
) (4.1)
Остальные потенциалы целесообразно рассматривать как функции G(T,P).
Тогда задача минимизации этих потенциалов сводится к решению конечного числа задач минимизации энергии Гиббса. Система будет находиться в равновесии, когда ее функция энергии Гиббса принимает минимальное значение. Для гетерогенной системы из n зависимых компонентов, которая одновременно может включать конденсированные однокомпонентные и многокомпонентные фазы, а также газовую смесь, изобарно-изотермический потенциал можно записать:
G(x)=
+
+lnP+ln
(4.2),
где
G–
эмпирическая функция, заменяющая
неизвестное истинное значение энергии
Гиббса; R–
универсальная газовая постоянная;
–
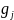эмпирические функции, за-меняющие
неизвестные истинные значения энергии
Гиббса зависимых компонентов системы;
–
число молей зависимого компонента;
–
число молей зависимых компонентов в
фазе
;
P– давление;
–
коэффициент активности зависимого
компонента j
в соответствии с принятой системой
отсчета
.
Система уравнений баланса масс системы:
; i=1,2,…,n (4.3)
где
–
число молей независимого компонента i
в одном моле зависимого компонента j;
–
общее число молей независимого компонента
i в системе.
С помощью наложения ограничений на мольные количества зависимых компонентов системы можно детально учесть эмпирическую информацию об особенностях, протекающих в ней процессов, т.е. ставить и решать физико-химические задачи с заранее предопределенной неравновесностью. Тогда условие (1.3) заменяется неравенством:
≤
≤
, (4.4)
где и – заданные нижние и верхние ограничения на мольные количества а j-го зависимого компонента;
В изобарно-изотермических условиях равновесный состав системы находится минимизацией непрерывной скалярной функции (4.2) на множестве ограничений, задаваемых уравнениями баланса масс (4.3) и условиями (4.4):
=argminG(x), (4.5)
Верхняя крышечка над обозначает оптимальное решение.
Действительные значения неизвестны и не могут быть определены экс-периментально или рассчитаны теоретически. В практических расчетах используются функции, заменяющие значения в выбранном стандартном состоянии и системе отсчета, такие, чтобы замена не влияла на конечный результат вычислений. Эта задача сводится к замене в выражении
G (T, P) =H (T, P)-TS (T, P) (4.6)
неизвестной абсолютной функции энтальпии на приращение энтальпии, которое может быть определено на основании обработки данных калориметрии.