12. Закон полного тока для магнитного поля в вакууме и веществе.

Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В): циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной μ_о на алгебраическую сумму токов охватываемых этим контуром: 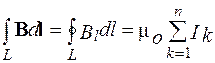Закон полного тока для магнитного поля в веществе является обобщением вышеприведенного закона с учетом как макротоков, так и микротоков:

13. Уравнения Максвелла для электромагнитного поля.

Максвелл высказал гипотезу, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в контуре.

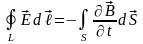
Из уравнения, следует, что изменяющееся магнитное поле порождает электрическое поле. Равенство называется первым уравнением Максвелла.

Согласно рассмотренному выше первому уравнению Максвелла изменяющееся магнитное поле порождает вихревое электрическое поле. Максвелл считал, что электрическое и магнитное поля всегда связаны, поэтому изменяющееся со временем электрическое поле должно приводить к появлению магнитного поля. Током смещения Максвелл назвал переменное электрическое поле. Плотность тока проводимости вблизи обкладок конденсатора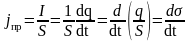 . Электрическое поле можно характеризовать вектором электрического смещения D=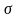 . – поверхностная плотность зарядов. При расчете магнитных полей необходимо брать полный ток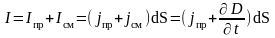 Понятие тока смещения и полного тока дает возможность утверждать, что все цепи переменного тока всегда замкнуты.Тогда обобщенная теорема о циркуляции вектора напряженности запишется в виде Это второе уравнение Максвелла, утверждающее факт появления вихревого магнитного поля при всяком изменении электрического поля

14. Волновое уравнение для электромагнитного поля. Энергия электромагнитных волн. Вектор Умова-Пойнтинга.

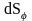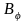
Из теории Максвелла следует, что образование переменного во времени электрического поля всегда вызывает возникновение вихревого магнитного поля и, наоборот. Векторы напряженностей и переменного электромагнитного поля для однородной и изотропной среды вдали от заряда и токов удовлетворяют волновым уравнениям 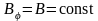Уравнениям удовлетворяют, в частности, плоские монохроматические электромагнитные волны, описываемые уравнениями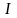 где Е₀ и Н₀ – амплитудные значения полей; ω – циклическая частота колебаний; – волновое число; – начальные фазы колебаний в точках с координатой х = 0.

Электромагнитные волны переносят энергию. Объемная плотность энергии складывается из плотности энергии электрического поля 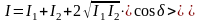и плотности энергии магнитного поля , следовательно, энергия единицы объёма электромагнитного поля равна их сумме, т.е.

Умножив плотность энергии на скорость распространения волны в вакууме –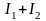 , получим модуль плотности потока энергии:

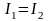
Направление вектора 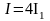совпадает с направлением переноса энергии, поэтому вектор плотности потока электромагнитной энергии можно представить как векторное произведение Вектор называется вектором Умова–Пойнтинга. Модуль вектора равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.