Тесты на гетероскедастичность
Рис.23. Остатки модели
Воспользуемся тестом Вайта, чтобы точно определить наличие/отсутствие гетероскедастичности.
Рис.24. Тест Вайта на гетероскедастичность, Y от X1.
Итак, нулевая гипотеза: гетероскедастичность в остатках отсутствует.
P
– значение =
.
Следовательно, нулевую гипотезу отклоняем
в пользу альтернативной: с вероятностью
95% гетероскедастичность в остатках
есть.
Рис.25. Тест Бриша-Пэгана на гетероскедастичность, Y от X1.
P – значение =0,0737983 > 0,05. Следовательно, нулевая гипотеза подтверждается – гетероскедастичность в остатках отсутствует.
Итак, два теста показали разные результаты. Поэтому, проведем еще один тест Бриша - Пэгана (робастный вариант).
Рис.26. Тест Бриша-Пэгана на гетероскедастичность, Y от X1.
P – значение = 0,647263 > 0,05. Следовательно, нулевая гипотеза подтверждается – гетероскедастичность в остатках отсутствует.
В нашем случае большинство тестов говорят об отсутствии гетероскедастичности.
Тесты на автокорреляцию остатков
Посчитаем коэффициент корреляции.
Рис.27. Коэффициент автокорреляции первого порядка остатков
Нужное нам значение:
.
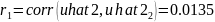Проверим коэффициент на значимость.
Поскольку P
– значение = 0.9274 > 0,05, коэффициент
незначим, и автокорреляции в остатках
нет.
Тест на нормальность остатков
Рис.28. Тест на нормальность распределения остатков
Рис.29. Тест на нормальность распределения остатков
P
– значение =
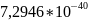< 0,05. Нулевая гипотеза отвергается с
вероятностью 95%, остатки модели не
распределены нормально.
Тест Рамсея
Рис.30. Тест Рамсея
P – значение > 0,05. Нулевая гипотеза подтверждается, и с вероятностью 95% в модели присутствуют все объясняющие факторы.
Регрессионная модель
Рис.31. Результаты оценки регрессии
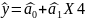
Модель имеет вид:
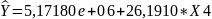
Проверим гипотезы о незначимости параметров модели:
Константа (
Нулевая гипотеза ( ): в генеральной совокупности константа незначима.
Альтернативная гипотеза ( ): , в генеральной совокупности константа значима.
P – значение = 0,0400 < 0,05. Следовательно, нулевая гипотеза отклоняется с вероятностью (1-0,05) = 0,95, или 95%, то есть константа модели значима.
Коэффициент перед X2 (
, в генеральной совокупности коэффициент перед X4 незначим.
, в генеральной совокупности коэффициент перед X4 значим.
P
– значение =
.
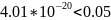Следовательно,
нулевая гипотеза отклоняется в пользу
альтернативной с вероятностью (1-0,05) =
0,95, или 95%, то есть коэффициент модели
при X2 значим.
Проверим гипотезу о незначимости модели в целом.
: все параметры модели (кроме константы) равны друг другу и равны нулю, т.е. модель в целом незначима.
: все параметры модели (кроме константы) не равны друг другу и не равны нулю, т.е. модель в целом значима.
P-значение (F) = . Следовательно, нулевая гипотеза отклоняется в пользу альтернативной с вероятностью 95%, то есть модель в целом значима.
Оценка качества модели по графикам
Рис.32. График «прогноз-реализация» для модели
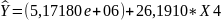
Рис.33. Линия регрессии
Для того чтобы точно определить аномальные точки, посмотрим отчет по остаткам.
Судя по графику можно предположить, что аномальными являются IOC.BO, PPG, что подтверждается данными из отчета по остаткам. (рис.34).
Рис.34. Выдержка из отчета по предсказанным значениям
С помощью отчета по значимым наблюдениям определим значимые наблюдения.
Рис.35. Выдержка из отчета по значимым наблюдениям
Итак, наблюдается одно значимое наблюдение: 0857.НК.
Проверка наличия ошибок спецификации модели