Определение дисперсии

№ n/n	xi	ni	xini	хi -	(хi - 2	(хi - 2ni
1	2	3	4	5	6	7
1	1,25	3	3,75	-0,11	0,0121	0,0363
2	1,30	5	6,50	-0,06	0,0036	0,0180
3	1,32	6	7,92	-0,04	0,0016	0,0096
4	1,36	9	12,14	0,00	0,0000	0,0000
5	1,38	8	11,04	0,02	0,0004	0,0032
6	1,40	5	7,00	0,04	0,0016	-,0080
7	1,42	4	5,68	0,06	0,0036	0,0144
8	1,45	3	4,35	0,09	0,0081	0,0243
всего	-	43	58,48	-	-	0,1138

= = 1,36 : σ² = = 0,0026

Среднее квадратичное отклонение σ – извлечь корень квадратный из дисперсии и учесть только положительный корень: σ = √ σ². (3);

σ = √0,0026 = 0,05 с.

Объединим два основных параметра вариационного ряда - и σ в виде следующего интервала: ± σ = (1,36 ± 0,05) с.

Коэффициент вариации v – параметр вариационного ряда для определения характера рассеивания по формуле v = · 100%;

v = 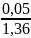· 100% = 3,68%; это означает, что рассеивание показателей относительно средней арифметической составляет 3,68%.

Основные вариационные ряды бывают трех видов: 1- простые упорядоченные; 2- дискретные; 3- интервальные. В дискретных рядах варианты выражаются одним числом (1,36; 0,1138). Простой упорядоченный ряд представляется только вариантами : ± σ = 1,36 ± 0,05 и имеют упрощенную форму определения параметров ряда. В интервальном ряду каждый вариант выражается интервалом, величина интервала может избираться произвольно: чем больше интервал, тем менее точные показатели ряда.

Интервальный ряд при k = 0,10

№ n/n	xi	ni
1	1,25 . . . 1,35	14
2	1,35 . . . 1,45	29
всего	-	43

Графическое изображение рядов имеет два основных представления: 1- полигон; 2- гистограмму. Дискретный ряд отражает полигон

Графическое изображение вариационного ряда Результаты, см

ЦЕЛЬ: Научиться находить среднюю арифметическую величину , дисперсию σ², среднее квадратическое отклонение σ, коэффициент вариации υ.

Самостоятельная работа

Задача: научиться находить среднюю арифметическую величину , дисперсию σ², среднее квадратическое отклонение σ, коэффициент вариации υ.

1. Задание студентам: письменно ответить на вопросы: 1) Определение понятия «ранжирование»; 2) Вариационный ряд состоит из …..; 3) Дисперсия указывает на …. ; 4) Назвать виды вариационных рядов.

2. Скорость плавания (м/с) у 20 пловцов составила (табл.22) .

Таблица 22.

1,00	1,26	1,20	1,32	1,12	1,26	1,30	1,30
1,12	1,20	1,00	1,20	1,12	1,00	1,12	1,26
1,00	1,20	1,32	1,12

Составить вариационный ряд.

3. Рассчитать среднюю арифметическую величину . По формуле

=

4. Вычислить дисперсию σ² по формуле: σ² = ;

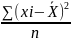5. Определить параметры вариационного ряда – среднего квадратического отклонения σ. По формуле σ = √ σ².

6. Вычислить коэффициент вариации v – параметр вариационного ряда для определения характера рассеивания по формуле v = · 100%;

7. Графически построить гистограмму (столбиковую диаграмму) на основе интервального ряда.

Сделать выводы по работе.

Лабораторная работа № 3. (2 часа)

ТЕМА: Точность измерений.

ЦЕЛЬ: Изучить и научиться пользоваться погрешностями измерений.

Ход работы: