1.2. Диффузия примесей при термообработке

Перераспределение примесей в пространстве системы Si - SiO₂ при термообработке описывается уравнением непрерывности, которое может быть записано следующим образом

, (1.8)

где C - концентрация примесей;

S(t) - замкнутая поверхность (функция времени, t);

V(t) - замкнутый объем по S(t);

- вектор потока примесей;

- единичный вектор, нормальный к S(t);

g - скорость генерации примесей;

l - скорость потерь примесей.

Левая часть уравнения (1.8) представляет собой скорость изменения содержания примеси в некотором объеме V(t) и определяется как скорость генерации примеси в этом объеме минус уход примеси через поверхность S(t), ограничивающую объем V(t). Использование уравнения непрерывности в интегральной форме упрощает обработку изменения объема, происходящего при окислении кремния и в процессе эпитаксиального наращивания. Члены в уравнении (1.8), описывающие процессы генерации и потерь, включены для учета эволюции состояний примесных атомов в кристаллической решетке кремния, как, например, в случае мышьяка, когда атомы могут существовать как в межузельном, так и кластерном состояниях.

Для одномерного потока уравнение (1.8) можно записать в виде

, (1.9)

где , (1.10)

. (1.11)

Здесь y - направление, перпендикулярное поверхности кремниевой подложки (оно положительно для направлении внутрь подложки), а поток F(y) положителен в y- направлении. В физическом смысле поток примесей может возникать из-за термической диффузии, явлений на поверхности раздела, а также вследствие модификации поверхности раздела при окислении кремния и эпитаксии.

1.2.1. Диффузионный поток

Диффузия в твердом теле представляет собой физическое явление, ответственное за перераспределение примесей при высокотемпературных обработках. В любой точке y диффузионный поток F_D(y) примесей связывается с их концентрацией и градиентом диффузии посредством модифицированного первого закона Фика.

Для одномерного потока это соотношение имеет вид

, (1.12)

где D(y) - коэффициент диффузии примеси. Если предположить, что миграция примесей осуществляется только посредством диффузии отдельных атомов, то внутри материала отсутствуют как генерация, так и потери примесей. Следовательно, уравнение сохранения количества примесей примет вид

. (1.13)

Предполагая постоянство коэффициента диффузии, получим хорошо известное выражение для второго закона Фика посредством подстановки (1.10) и (1.12) в (1.13) и дифференцирования по y. Тогда уравнение (1.13) принимает вид

. (1.14)

Второй закон Фика достаточно адекватен для расчета диффузионного перераспределения примеси при низкой концентрации. Однако этот закон не выполняется, когда концентрация примеси возрастает до или выше концентрации собственных носителей заряда n_i(T) в полупроводнике. На рис.1.3 представлен график зависимости n_i от температуры, который используется в SUPREM II [27]. Кроме того, уравнение (1.12) может не выполняться даже при низкой концентрации, если присутствуют другие примеси в кремнии с высокой концентрацией.

Подробный анализ современных представлений и моделей диффузии примесных атомов в кремнии содержится в обзоре [28].

Одна из первых попыток объяснить диффузионное перераспределение примесей в высоколегированном полупроводнике состояла в включении электрического поля и введении эффекта влияния свободных носителей на перераспределение примесей в процессе высокотемпературной обработки [29]. Этот подход подобен описанию амбиполярной диффузии в плазме. В этом случае коэффициент диффузии является функцией концентрации примеси и определяется выражением

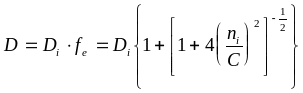, (1.15)

где D_i - собственный коэффициент диффузии примесей. Как видно из выражения (1.15), максимальное значение f_e равно 2 для C >> n_i. Однако этот факт не объясняет увеличения коэффициента диффузии до величин порядка 10...20, что часто наблюдается для большинства примесей.

Явление несобственной диффузии примеси является результатом миграции примеси посредством взаимодействия с заряженными точечными дефектами в кремнии [30]. Большинство примесей диффундирует в кремнии посредством взаимодействия с такими дефектами кристаллической решетки, как вакансии и межузлия. Таким образом, коэффициент диффузии примесей пропорционален концентрации точечных дефектов. Хотя концентрация нейтральных дефектов при любой температуре зависит от концентрации примеси (но не превышает концентрацию атомов кремния), концентрация дефектов в различных зарядовых состояниях (которые должны находиться внутри запрещенной зоны кремния) зависит от положения уровня Ферми в запрещенной зоне и, следовательно, является функцией концентрации примеси.

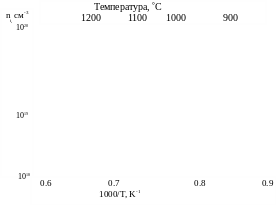
Рис.1.3. Зависимость от температуры концентрации

свободных носителей заряда в кремнии

В работе [31] проанализированы экспериментальные результаты по диффузии примесей в кремнии в предположении, что эффективный коэффициент диффузии должен быть суммой нескольких коэффициентов диффузии, каждый из которых учитывает взаимодействие примеси с различными зарядовыми состояниями вакансий кристаллической решетки. Эффективный коэффициент диффузии может быть, следовательно, представлен как

, (1.16)

где D^V - коэффициент диффузии, обусловленный каждым из приведенных выше зарядовых состояний вакансий, (v:=, -, ^х, +, т.е. двукратно заряженная, однократно заряженная, нейтральная и положительно заряженная вакансия), а [V^V] - концентрация вакансий в каждом заряженном состоянии, нормализованная на собственную концентрацию вакансий в соответствующем зарядовом состоянии. Используя больцмановское приближение, можно рассчитать нормализованные концентрации вакансий

, и , (1.17)

где n - концентрация свободных электронов. Следовательно, для собственного полупроводника (n=n_i) уравнение (1.16) принимает вид

, (1.18)

т.е. собственный коэффициент диффузии является суммой коэффициентов диффузии, обусловленных различными зарядовыми состояниями вакансий.

Данная модель является основой для описания диффузионного перераспределения примесей в программе SUPREM II. За исключением фосфора, предполагается, что только нейтральные или однократно заряженные вакансии ответственны за коэффициент диффузии примесных атомов. В программе SUPREM II используется специальная форма представления коэффициента диффузии

, (1.19)

где D_i - собственный коэффициент диффузии, а f_v=n/n_i поправочный коэффициент для доноров и n_i /n - для акцепторов. Следовательно, в собственном полупроводнике f_v=1 и D=D_i. С другой стороны, для примесных полупроводников физическое значение параметра  может быть выведено из уравнений (1.16), (1.17) и (1.19), что дает

и .

Таким образом, коэффициент =D_V / D_X является показателем эффективности заряженных вакансий относительно нейтральных вакансий при диффузии примеси. На рис.1.4 приведен график зависимости нормализованного коэффициента диффузии D/D_i от f_v. Очевидно, что для любого примесного элемента коэффициент  зависит от температуры, однако эти зависимости к настоящему времени отсутствуют. Рекомендуемые значения (используемые в программе SUPREM II по умолчанию): =3 для бора и =100 для мышьяка, в то время как для фосфора используется совершенно другая модель, которая будет описана ниже. Для других примесей величина  неизвестна и по умолчанию равна 1.

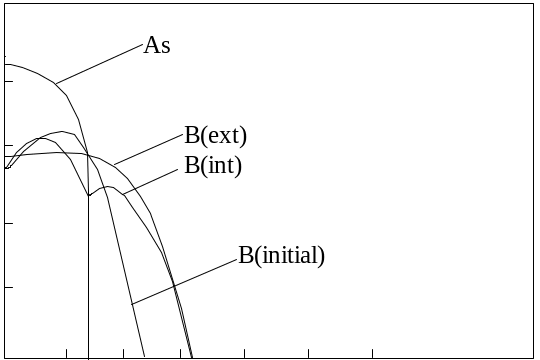
Хорошо известно, что при наличии в кремнии разных примесных атомов существует электрическое взаимодействие между ними [32]. На рис.1.5 иллюстрируется случай, когда мышьяк с высокой концентрацией влияет на распределение бора. В программе SUPREM II это взаимодействие моделируется посредством использования уравнения (1.10) для вычисления потока примесей. В примере, представленном на рис.1.5, диффузионный поток бора в области с высокой концентрацией примеси n-типа проводимости уменьшается, т.к. f_v(B)=n_i/n0, тогда как на краю профиля распределения мышьяка наблюдается падение концентрации из-за быстрого изменения f_v и, следовательно, коэффициента диффузии бора.

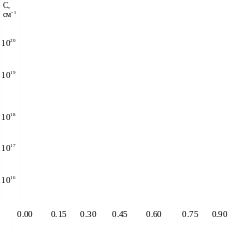
Фосфор. Модель, используемая в SUPREM II для диффузионной миграции фосфора, представлена в работе [33]. Модель описывает с приемлемой точностью образование ступеньки в профиле распределения фосфора (kink-effect), а также эффект смещения базы, обычно наблюдаемый при диффузии фосфора с высокой концентрацией в области эмиттера при биполярной технологии. Согласно этой модели физическое объяснение таких аномальных эффектов состоит в повышении концентрации вакансий в кремнии, вызванном диссоциацией ионизированных пар вакансий, которые движутся к кремниевой подложке. Типичный профиль распределения фосфора с высокой концентрацией состоит из трех частей, которые изображены схематически на рис.1.6,а:

Рис.1.4. Нормализованный коэффициент диффузии в зависимости

от нормализованной концентрации носителей для различных значений 

(Глубина, мкм)

Рис.1.5. Эффекты влияния высокого уровня легирования мышьяка

на перераспределение бора

B (initial) - исходное распределение бора после имплантации;

B (int) и B (ext) – профили распределения бора после термообработки

в присутствии мышьяка и без него соответственно;

As – профиль распределения мышьяка

1. Поверхностная область, в которой диффузия фосфора осуществляется посредством взаимодействия с нейтральными вакансиями и с вакансиями, имеющими двукратный заряд, формирующими P⁺V⁼ пары. В этой области коэффициент диффузии фосфора определяется выражением

, (1.20)

где n_i - концентрация свободных электронов, вычисляемая из полной концентрации фосфора с использованием выражения (1.11). Следовательно, в этой области коэффициент диффузии фосфора монотонно уменьшается (см. рис.1.6, а). Конец этой области лежит в точке, где уровень Ферми падает ниже 0.11 эВ относительно зоны проводимости; эта точка определяется как основной уровень для дважды ионизированных вакансий. Это имеет место при характеристической концентрации электронов, n_e, определяемой выражением

. (1.21)

2. Область хвоста, где коэффициент диффузии D_TAIL повышается относительно собственного значения вследствие пересыщения кристаллической решетки кремния вакансиями из-за диссоциации пар P⁺V⁼. В этой области коэффициент диффузии описывается выражением

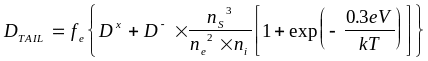, (1.22)

где n_s - концентрация поверхностных электронов.

Это уравнение следует рассматривать в качестве эмпирически подогнанного к экспериментальным результатам. Как видно из рис.1.6а, коэффициент диффузии в хвостовой части очень сильно зависит от n_s и, следовательно, от концентрации фосфора на поверхности.

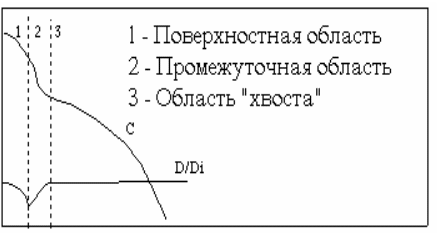
ГЛУБИНА

Рис.1.6, а. Типичный профиль распределения концентрации (С) фосфора

с выделением трех областей. Показано также локальное распределение коэффициента диффузии фосфора (D/D_i)

Поскольку данная модель предсказывает существование пересыщения вакансионных дефектов в объеме полупроводника [34], для других примесей в кристаллической решетке кремния под областью высокой концентрации фосфора также проявляется эффект усиления диффузии других примесей, примерно одинаковый по сравнению с эффектом, проявляющимся для атомов фосфора. Для этого в программе SUPREM II вводится коэффициент f_enh, задаваемый выражением

, (1.23)

на который умножается собственный коэффициент диффузии, D^x, другой примеси в присутствии фосфора. Такой подход позволяет не только моделировать эффект сдвига базы, но и предсказывать усиление коэффициента диффузии других примесей как, например, мышьяк или сурьма, которые могут присутствовать в скрытом слое коллектора при формировании биполярного транзистора.

3. Начало области хвоста определяется следующим образом. При использовании анализа Больцмана-Матано профиля фосфора при высоком уровне легирования [33, 35] было обнаружено, что существует промежуточная область между поверхностью и хвостом, где коэффициент диффузии возрастает пропорционально (n\n_i). Этот эмпирический факт используется в SUPREM II для определения начала хвостовой области. Коэффициент диффузии, рассчитываемый в конце поверхностной области (где n=n_e ), умножается на величину (n_i/_/n)² по мере увеличения глубины от поверхности, пока не будет достигнута точка, где коэффициент диффузии не достигнет значения D_. Именно в этой точке предполагается начало хвостовой области.

Из уравнения (1.23) видно, что эта модель предсказывает монотонное увеличение коэффициента диффузии фосфора с увеличением поверхностной концентрации (по крайней мере в хвостовой области). Известно, что поверхностная концентрация увеличивается по крайней мере до 3-4x10см^-3 при уменьшении коэффициента диффузии в хвостовой области. Этот эффект можно объяснить [36] сужением ширины запрещенной зоны кремния, обусловленным напряжением кристаллической решетки из-за высокой концентрации фосфора. В SUPREM II этот эффект напряжения кристаллической решетки моделируется посредством увеличения концентрации собственных носителей в соответствии с формулой

, (1.24)

, (1.25)

где Eg - сужение ширины запрещенной зоны, C_TS - полная поверхностная концентрация фосфора.

Очевидно, что n_e должно также увеличиваться на ту же величину. Важность включения в модель эффекта напряжения кристаллической решетки иллюстрируется рис.1.6 б, где рассчитанные профили диффузионного перераспределения фосфора (с и без  Eg ) сравниваются с экспериментальными данными.

Еще один дополнительный эффект влияния напряжения кристаллической решетки на коэффициент диффузии имплантированного фосфора включен в программу SUPREM II. Коэффициент диффузии фосфора уменьшается при увеличении дозы имплантации, что, вероятно, обусловлено разупорядочением кристаллической решетки в процессе имплантации. Следовательно, в случае ионно-имплантированного фосфора добавочное сужение ширины запрещенной зоны вычисляется из уравнения

, (1.26)

где Q_P - доза имплантации фосфора.

C, см^-3

0 0.2 0.4