1.4. Коши теоремасы

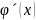Коши теоремасы (функциялардың ақырғы өсімшелері туралы). Егер мына үш шарт: 1) f(x) пен функциялары сегментінде үзіліссіз, 2) ең болмағанда (a, b) интервалында олардың туындылары f´(x) пен ақырлы, 3) (a, b) интервалында 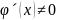орындалса, (a, b) интервалында ең болмағанда бір нүкте , c нүктесі, табылады және

теңдігі орындалады.

Дәлелдеу. Әуелі

(9)

болатынын дәлелдедік.

Шынында да, яғни болады деп жорысақ, 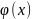функциясы Ролль теоремасының барлық шарттарын қанағаттандыратын болады да, (a, b) интервалының ең болмағанда бір нүктесінде нольге айналар еді. Олай болушылық Коши теоремасының үшінші шартына қайшы. Демек, (9) шарты міндетті түрде орындалады.

Сол себепті (8) теңдік мағынасыздыққа айналмайды. Сондықтан бұл теңдіктің (a, b) интервалындағы қандайда болса бір с нүктесінде орындалатындығын дәлелдесек болады.

Бұл мақсатта сегментінде анықталған мына көмекші функцияны қарастыралық:

Ф(x) = f(x) – f(a) -

f(x) пен функцияларының сегментінде үзіліссіздігі және олардың (a, b) интервалында ақырлы туындылары бар болу себепті (10) функция да сол шарттарды қанағаттандыратыны айқын. Сонан кейін:

Ф(a) = f(a) – f(a) -

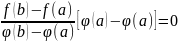
және

Ф(b) = f(b) – f(a) -

яғни

Ф(a) = Ф(b).

Бұдан (10) функцияның сегментінде Ролль теоремасының барлық шарттарын қанағаттандыратыны, сондықтан да (a, b) интервалында ең болмағанда бір нүктеде, с нүктесінде болатынын көреміз.

Ал

Ф´(x) = f´(x) -

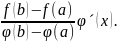
Олай болса:

Ф´(c) = f´(c) -

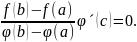
яғни

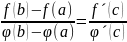
болады, дәлелдемекшіміз де осы болатын.

(8) теңдікті Коши формуласы деп атайды.

Коши теоремасы осы теореманың алдында ғана дәлелденген Лагранж теоремасының онан ары жалпылануы болып табылады. Оған дәлел: егер 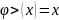десек те Коши теоремасындағы шарттар бұзылмайды.

Бұл жағдайда

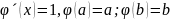
болады да, Кошидің (8) формуласы мына түрге келеді:

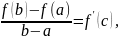
яғни Коши формуласы 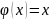болған жағдайда Лагранж формуласына айналады.

1-ескерту. Коши формуласы және Лагранж формуласы тек a болғанда ғана дұрыс болып қана қоймай, a болғанда да дұрыс болып қала береді.

2-ескерту. Дәлелденген Ролль, Лагранж, Коши теоремаларында туындының аргументі тәуелсіз айнымалының қандай болса да бір орташа с мәні болып табылады. Сондықтан туындылардың сәйкес мәндерін де орташа деп, ал сол аталған теоремаларды “орташа мәндер теоремалары” дейді.

3-ескерту. (8) қатынасы 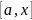кесіндісінің кез келген нүктесінде дұрыс, яғни

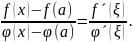
Мысалдар. 1-мысал. 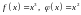функциялары үшін Коши формуласын жазу керек және 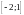кесіндісіндегі с –нің мәнін анықтау керек.

Шешуі. Шарт бойынша:

Сол сияқты,

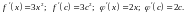
Коши формуласына қойып, мынаны аламыз:

бұдан,

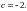
2-мысал. f(x) = 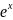және g(x) = функциялары 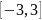кесіндісінде Коши теоремасы шарттарын қанағаттандыра ма?

Шешуі. Жоқ, себебі: екеуі де берілген аралықта үзіліссіз дифференциалданатын болғанымен, g´(x) = 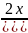туындысы

x = 0 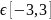нүктесінде 0-ге тең.