20. Частотная модуляция. Спектр сигнала с угловой модуляцией.

При частотной модуляции по закону модулирующего (передаваемого) сигнала изменяется мгновенное значение частоты ω₁(t) носителя: . Мгновенное значение частоты ω₁ модулированного колебания определяется выражением , где - коэффициент пропорциональности, устанавливающий связь между модулирующим сигналом и изменением частоты носителя; - частота немодулированного носителя. Полная фаза модулированного колебания определяется в виде . Отсюда видно, что при ЧМ имеет место изменение фазы колебания, т.е. ФМ. Получим выражение для частотно-модулированного сигнала: , где - девиация частоты (максимальное отклонение частоты от значения ); - индекс модуляции. Индекс частотной модуляции фактически равен максимальному отклонению фазы ЧМ-колебания, т.е. m_ЧМ =_max. Он не зависит от средней ω₁ (немодулированной) частоты, а определяется исключительно величиной девиации частоты и модулирующей частотой .

Спектры сигнала с угловой модуляцией

Выражение для сигнала, модулированного по частоте или фазе . Рассмотрим случай, когда m – любая величина. Для этого функции sin(msinΩt) и cos(msinΩt) разложим в тригонометрические ряды. В теории Бесселевых функций доказываются следующие соотношения: где J_n(m) – Бесселева функция первого рода n-го порядка от аргумента m. Перепишем выражение для сигнала в виде

Заменив в этом выражении произведения косинусов и синусов суммами, получим

Таким образом, при угловой модуляции спектр сигнала состоит из бесконечного числа боковых частот, отличающихся от несущей частоты ω₁ на  n.

Примерный вид спектра сигнала с угловой модуляцией одним тоном  при m=3 и U_ω1=1 В представлен на рисунке. По мере удаления от ω₁ амплитуды боковых составляющих уменьшаются.

21. Фазоимпульсная модуляция

П ри ФИМ по закону изменения передаваемого сигнала с(t)=U_sin(t) изменяется величина временного сдвига относительно тактовых точек (рисунок 3.5)

Если у немодулированного импульса фронт соответствует моменту времени -τ/2, а спад – моменту времени +τ/2, то для модулированного импульса эти моменты будут (рис. 3.6):

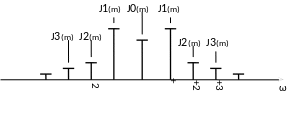
где - наибольшее смещение фронта.

где ω₁=m_ФИМ – индекс модуляции при ФИМ.

Из анализа выражения следует, что спектр сигнала при ФИМ содержит постоянную составляющую, составляющую с частотой модулирующего сигнала , основную гармонику с частотой ω₁(k=1) и кратные ей высшие гармоники с частотами kω₁, вокруг которых размещаются полосы боковых гармоник с частотами kω₁n (рисунок 3.7). Необходимая полоса частот ω_ФИМ=2 /. Доля мощности, заключенная в составляющих с частотами выше ω_B, настолько мала, что эти составляющие можно не учитывать.

22. Двукратная модуляция ам-чм.

АМ-ЧМ-сигнал. При данном сигнале поднесущая промодулированная по амплитуде, модулирует носитель по частоте. В соответствии с определением частотной модуляции можно записать выражение для АМ-ЧМ-сигнала в виде

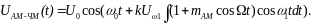
Спектр АМ-ЧМ можно построить по следующему правилу: строится спектр полезного сообщения C(t), затем спектр полезного сообщения переносится на частоту поднесущей по правилам АМ сигнала, а потом полученный спектр переносится на несущую частоту по правилам ЧМ-сигнала.

Спектр, построенный по рассмотренной выше методике, приведен на рисунке 4.41.

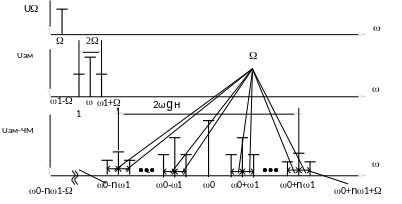
Рисунок 4.41 – Процесс построения спектра АМ-ЧМ-сигнала

Следует отметить, что спектр, построенный по данной методике, дает представление о частотном составе спектра, позволяет определить полосу частот, занимаемую сигналом, но не дает возможности определить амплитуды отдельных гармонических составляющих.

Определим полосу частот, занимаемую АМ-ЧМ-сигналом, как разность частот между верхней и нижней боковыми составляющими.

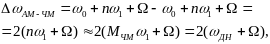где

- индекс частотной модуляции несущего сигнала; - девиация частоты носителя.