Четверте рівняння Максвела

Четверте рівняння Максвела в інтегральній формі співпадає із законом Гауса для магнітного поля, який можна сформулювати наступним чином. Потік вектора через будь-яку поверхню S рівний нулю: . Це означає, що не існує ліній вектора , які тільки входять в замкнуту поверхню S (чи навпаки, тільки виходять із поверхні S): вони завжди пронизують її. Це є четверте рівняння Максвела в інтегральній формі. В результаті перетворень можемо отримати диференціальну форму: .

Це показує, що в природі відсутні магнітні заряди. З цього рівняння також слідує, що лінії вектора (силові лінії магнітного поля) являються завжди неперервними.

Резюме:

1). Максвел ввів струм зміщення.

2). Результатом 1 і 3 рівнянь Максвела є закон збереження заряду – вивести.

2.4. Електромагнітні властивості середовищ

Вектори електричної та магнітної індукцій і , а також густина струму провідності зв’язана з напруженостями поля і співвідношеннями, які залежать від властивостей середовища. Зазвичай існують зв’язки:

, , (2.15)

Найчастіше процеси в середовищі вважаються локальними і безінерційними, для яких:

–матеріальні рівняння, (2.16-2.18)

де – відносна діелектрична проникливість; – відносна магнітна проникливість;

– питома провідність.

Тут j=σE – закон Ома в диференціальній формі.

Поляризація і намагнічування

Нехай електромагнітне поле вакууму має і . Тоді і .

Якщо ж поле існує в деякому середовищі, то:

, (2.19)

де – поляризованість; – намагніченість. Звичайно, що і . В більшості випадків цим співвідношенням можна надати простої форми:

, , (2.20)

де і – безрозмірні коефіцієнти: електрична і магнітна сприйнятливості середовища. Тоді

=1+ =1+ . (2.21)

Розрізняють випадки, де зустрічається лише намагнічування чи поляризація, це є:

– магніти, що характеризуються самостійним намагнічуванням та

– електрети, що характеризуються самостійною поляризованістю.

Для більшості середовищ . Але існують і такі, для яких магнітна проник-ливість не відповідає цій умові. В залежності від усі метали поділяють на:

1. Діамагнетики: , наприклад, мідь: =0.99999044;

2. Парамагнетики: , наприклад, алюміній: =1.00002227;

3. Феромагнетики: , наприклад, залізо: >1000.

Електропровідність

В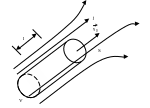 иділимо елементарний об’єм V . Візьмемо закон Ома в диференціальній формі: .

Проінтегруємо цей вираз за малим об’ємом V:

.

Тут величина – струм провідності; – падіння напруги на відстані l. Тоді отримаємо:

I·R=U. (2.21)

Це є закон Ома для ділянки кола, де R=l/S – електричний опір виділеної ділянки кола (або середовища). R вимірюється в Омах [Ом], а питома провідність  – у Сіменсах/метр [См/м].

Нехай носії додатного заряду переміщуються зі швидкістю . При цьому існує струм із густиною j, який направлений як і . Тоді справедлива така формула:

. (2.22)

Довести формулу.

2.5. Типи середовищ в електродинаміці. Провідники і діелектрики

Вираз для густини повного струму (з використанням матеріальних рівнянь):

. (2.23)

Для ідеального діелектрика: ; а для ідеального провідника: .У випадку : зникає перший член . У випадку : другий член стає неважливим, у порівнянні з першим. Тоді, якщо

– провідник, а якщо – ізолятор (або діелектрик).

Якщо поле E=E_mcost – гармонійне, то можна отримати наступне співвідношення для амплітуд j_m і : , (2.24)

де – циклічна (колова) частота . Тоді виконується така умова:

. (2.25)