
- •41.Наибольшее и наименьшее значение функции на отрезке.
- •42.Выпуклость функции. Точки перегиба.
- •44. Общая схема исследования функций и построения их графиков.
- •Определение, предел и непрерывность функции нескольких переменных.
- •Частные производные первого и высших порядков.
- •48.Определение экстремума функции двух переменных. Необходимые и достаточные условия экстремума функции двух переменных.
- •Первообразная функции и неопределенный интеграл.
- •54.Таблица основных интегралов
- •55. Интегрирование при помощи подстановки.
- •56.Интегрирование по частям.
- •Интегрирование рациональных функций. Метод неопределенных коэффициентов.
54.Таблица основных интегралов
Таблица содержит формулы, которые проверяются непосредственным дифференцированием.
1)
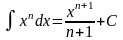 2)
2)
 3)
3)
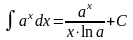
4)
 5)
5)
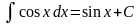 6)
6)
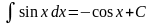
7)
 8)
8)
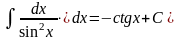
9)
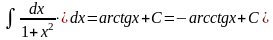 10)
10)
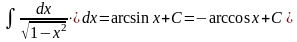
11)
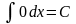 12)
12)

55. Интегрирование при помощи подстановки.
Метод интегрирования подстановкой можно разделить на три подгруппы методов, для которых справедлива общая формула –
![]()
После интегрирования выражения, которое содержит новую переменную, необходимо возвращаться к старой переменной.
непосредственная замена: Идея здесь такова, что путем замены мешающей части подынтегрального выражения получаем интеграл более простого вида или вообще табличный интеграл.
Найти интеграл
 -меняем корень на новую переменную
-меняем корень на новую переменную
2)поднесение под знак дифференциала.
Этот метод применяется тогда, когда под знаком интеграла стоит произведение, в котором какая-либо часть подынтегрального выражения может быть выражена через дифференциал другого сомножителя
![]()
3)метод интегрирование
подстановкой.
В этом случае
замена переменной носит несколько
искусственный характер, хотя суть метода
замены переменной
остается
прежней. Найти
интеграл
![]()

56.Интегрирование по частям.
![]()
Рекомендации по применению формулы интегрирования по частям
В качестве u берут функцию, производная от которой представляет более простое выражение, чем сама функция, а в качестве dv берут произведение оставшейся функции на dx, а затем берут первообразную от этой функции.
Случай 1. (Произведение многочлена на тригонометрическую или показательную функцию).
Если
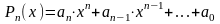 f(x)
- одна из функций: cos(ax+b);
f(x)
- одна из функций: cos(ax+b);
 ;
sin(ax+b),
то в качестве u
берут многочлен (u
= Pn(x);
f(x)dx
= dv)
и в этом случае интегрируем по частям
столько раз, какова степень многочлена.
;
sin(ax+b),
то в качестве u
берут многочлен (u
= Pn(x);
f(x)dx
= dv)
и в этом случае интегрируем по частям
столько раз, какова степень многочлена.
Случай 2. (Произведение многочлена на обратную тригонометрическую или логарифмическую функцию) Если f(x) - одна из функций: ln(ax+b), arctg(ax+b), arcctg(ax+b);то u=f(x); Pn(x)dx=dv. В этом случае по частям интегрируем только один раз.
Интегрирование рациональных функций. Метод неопределенных коэффициентов.

Если n<m, то дробь называют правильной; если n≥m, то дробь называют неправильной.
Простейшие дроби


IV-Для
нахождения интеграла
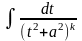 используют рекуррентную формулу,
которая позволяет свести нахождение
этого интеграла после (к-1)
шагов к
нахождению табличного интеграла.
используют рекуррентную формулу,
которая позволяет свести нахождение
этого интеграла после (к-1)
шагов к
нахождению табличного интеграла.
