§4. Интегралы движения в методе Лагранжа. Свойства симметрии пространства и времени. Законы сохранения.

Динамические переменные в методе Лагранжа – это обобщённые координаты и обобщённые скорости. Всего их 2n, они задают начальное состояние систем.

Интеграл движения – это функция динамических переменных и времени , сохраняющая своё значение при движении системы (в КП).

- постоянство означает, что полная производная по времени должна быть равна нулю:

При n=1 имеем:

, .

Рассмотрим замкнутую систему.

Замкнутая система материальных точек – это система точек, взаимодействующих между собой и не взаимодействующих с точками, не принадлежащими, данной системе.

1 .Для замкнутой системы реализуется принцип однородности времени.

Это означает, что мы по временной оси начало отсчёта можем выбрать произвольно. Допустим, мы вели наблюдения в течение времени , этот отрезок времени можно на оси t взять в любом месте, процесс не изменится. Вследствие однородности времени для замкнутых систем функция Лагранжа явно не зависит от времени, т.е.

Найдём производную функции Лагранжа по времени:

Подставим второе уравнение в первое:

В силу уравнения движения Лагранжа:

Тогда:

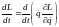
- интеграл движения, но только для стационарных связей.

В случае многих степеней свободы:

В случае стационарных связей кинетическая энергия есть квадратичная форма скоростей.

- коэффициенты, имеющие не обязательно смысл массы.

В силу теоремы Эйлера об однородных функциях:

=const, т.е. реализуется скалярный закон сохранения энергии

2.Однородность пространства.

Пространство называется однородным, если уравнения движения (эволюции) системы не зависят от трансляции (переноса как целого) системы в пространстве.

У равнения движения замкнутой системы инвариантны относительно пространственных трансляций системы как целого. В этом случае реализуется закон сохранения импульса:

или

, ,

Для замкнутой системы:

, т.е реализуется векторный закон сохранения импульса системы.

Иногда системы, будучи не замкнутыми, допускают трансляции вдоль некоторых осей. Например, система в однородном поле силы тяжести, допускает трансляции, в плоскости ортогональной вектору напряжённости этого поля -

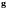
- у поверхности Земли.

3. Изотропность пространства.

Уравнения движения замкнутой системы не изменяются при вращении системы как целого относительно любой оси. Другими словами, уравнения движения инвариантны относительно вращения вокруг любой оси. В этом случае реализуется закон сохранения момента импульса:

- момент импульса материальной точки a.

, т.е реализуется векторный закон сохранения момента импульса системы.

Для незамкнутой системы существуют поля, допускающие вращение системы как целого относительно некоторых осей.

Пример:

Если выбрать z вдоль , то систему можно вращать как целое вокруг z, в данном поле будет сохраняться проекция момента импульса на направление поля.

Рассмотрим теперь центральное поле. Например, гравитационное поле Земли (сферически симметричное).

Центр Земли – это центр поля тяготения. Вращение вокруг любой оси, проходящей через центр симметрии, не меняет уравнения движения.