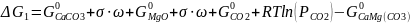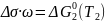Контрольные вопросы

1. Почему возникает необходимость моделирования процессов производства стали?

2. Какова природа взаимодействия металла со шлаком и в чем это проявляется?

3. Какой потенциал называется стационарным?

4. Какой потенциал называется равновесным?

5. Что называется электродной поляризацией (перенапряжением)?

6. Что называется коэффициентом распределения марганца между металлом и шлаком?

7. От чего зависит константа распределения марганца между металлом и шлаком?

8. Какие факторы влияют на скорость перехода марганца из металла в шлак в диффузионном режиме?

9. Перечислите определяемые по результатам опытов физические величины.

10. Выберите комбинации величин для построения регламентированных в работе графиков (Ось Х, Ось Y).

11. Перечислите физические величины, определяемые по результатам опытов.

12. Перечислите ожидаемые наблюдения по результатам работы.

13. Укажите количество электронов в электродной полуреакции перехода марганца (кремния, железа) через границу металл – шлак.

14. Укажите формы существования реагентов (кремний, марганец, железо) в фазах, в которых они присутствуют.

15. Последовательно перечислите этапы восстановления марганца (железа, кремния) и механизмы их реализации.

2.7 Изучение диссоциации доломита методом дифференциального термического анализа (Работа № 21)

2.7.1 Особенности процесса диссоциации доломита

Общие закономерности процессов диссоциации карбонатов обсуждены в разделе 2.4 «Термографическое изучение процессов диссоциации природных карбонатов (Работа № 16)». Чистый доломит является двойной солью угольной кислоты и имеет химическую формулу CaMg(CO₃)₂. Для природных доломитов в зависимости от месторождения характерно наличие различных примесных минералов: CaCO₃, CaSO₄, CaO, MgO, SiO₂, -содержание которых может достигать нескольких процентов. Для исследования более сложной по сравнению с карбонатом кальция системы требуется метод, позволяющий получить дополнительную информацию о системе, поэтому здесь использован метод дифференциального термического анализа, позволяющий в дополнении к значениям температур остановок оценить величины тепловых эффектов процессов.

Как и кальцит доломит является соединением с преимущественно ионными связями, в узлах кристаллической решетки которого чередуются ионы Ca²⁺, Mg²⁺ и CO₃^2-. Ион магния обладает наиболее сильным электростатическим полем, которое в сочетании с кинетической энергией при относительно небольшой температуре способно разрушить сложный анион CO₃^2-, при этом выделяется молекула углекислого газа и ион кислорода. В тесном пространстве кристаллической решетки доломита молекула углекислого газа начинает диффундировать в направлении менее плотной решетки, а ионы магния и кислорода перемещаются на небольшое расстояние в поисках себе подобных, формируя наноразмерные области оксида магния. Анионы угольной кислоты, удержавшиеся вблизи катионов кальция, образуют области кальцита такого же размера, поскольку число частиц кальция и магния в исходной решетке одинаково. Таким образом однородная однофазная кристаллическая система по мере диссоциации карбоната магния превращается в гетерогенную ультрамелкодисперсную. Происходящая при этом реакция предается уравнением:

CaMg(CO₃)₂ = CaCO₃ + MgO + CO₂. (1)

В этой записи подчеркивание использовано, чтобы отметить мелкодисперсное состояние фаз. При реализации процесса в отрытой установке в исходном состоянии такая система характеризуется четырьмя компонентами, включая и компонент «воздух», поскольку составляющие последнего – кислород и азот ни в каких реакциях не участвуют и в этом смысле неразличимы. Число степеней свободы:

с = 4 + 1 – 4 = 1

означает, что в системе может меняться только один параметр (температура) без изменения числа или природы фаз в новом состоянии равновесия.

Так продолжается до тех пор, пока равновесное давление СО₂ над доломитом не достигнет атмосферного давления. При этом весь воздух из системы будет вытеснен, число компонентов уменьшится до трех, а число степеней свободы станет равным нулю и до завершения процесса диссоциации карбоната магния температура меняться не сможет – наступит температурная остановка. В реальности по ряду причин температура вновь начнет расти раньше, чем произойдет полное разложение карбоната кальция.

С ростом температуры увеличение колебательной энергии движения частиц в кристаллической решетке кальцита в совокупности с дестабилизирующим действием электростатического поля катиона кальция приведет к разрушению аниона CO₃^2- уже в решетке карбоната кальция. Образующийся ион кислорода вместе с высвобождающимся ионом кальция будут образовывать новую самостоятельную фазу столь же мелкодисперсного кальцита, либо растворяться в уже имеющемся оксиде магния. Новый процесс передается уравнением:

CaCO₃ = СаО + CO₂. (2)

либо

CaCO₃ + MgO = (СаО + MgO) + CO₂. (3)

Здесь круглые скобки отражают нахождение реагентов в составе единого раствора. И в том и другом случае при давлении углекислого газа меньше атмосферного число компонентов равно четырем и равно числу фаз. Система имеет одну степень свободы, позволяющую ее нагревать без изменения числа фаз. При возрастании давления углекислого газа до атмосферного и вытеснения воздуха число степеней свободы уменьшается до нуля и наступает вторая температурная остановка.

Термодинамическое описание реакции (1) должно учитывать мелкодисперное состояние продуктов реакции. Известно, что энергия Гиббса дисперсного вещества включает дополнительное слагаемое, равное произведению межфазной энергии единицы поверхности (σ) на величину поверхности раздела (ω). Поэтому выражение для изменения энергии Гиббса в реакции (1) приобретает вид:

(21.1)

В этой формуле G⁰ – энергии Гиббса в стандартном состоянии, которые могут быть вычислены по термодинамическим данным, σ – межфазное натяжение на границе раздела оксида магния и кальцита, ω – площадь этой поверхности раздела, зависящая от размера дисперсных частиц, R – универсальная газовая постоянная, Т – абсолютная температура. Во время температурной остановки (Р_СО2 = 1) в равновесной системе изменение энергии Гиббса равно нулю, поэтому обобщенная характеристика поверхностных свойств и дисперсности системы (σ·ω) легко может быть вычислена по формуле:

(21.2)

Стандартное изменение энергии Гиббса в процессе 1 для температуры, отвечающей опытному значению первой температурной остановки, можно рассчитать, пользуясь термодинамической базой данных (TDHT) и специальными функциями для термодинамических расчетов.

Выражение для изменения энергии Гиббса для второго процесса в отсутствие образования оксидного раствора наряду со стандартным изменением энергии Гиббса процесса диссоциации кальцита должно включать сравнительно небольшую поправку, связанную с изменением межфазного натяжения (Δσ) на границе раздела при замене карбоната кальцитом.

(21.3)

В варианте образования раствора вместо нее должна быть учтена уже известная характеристика поверхностных свойств и дисперсности системы (21.2) и изменение энергии Гиббса при образовании раствора. Считая раствор идеальным и с одинаковой концентрацией компонентов (X_CaO = X_MgO = 0.5) получим следующее выражение:

(21.4)

Применяя это выражение (21.3) к описанию системы во время второй температурной остановки (Т₂) можем оценить добавку, связанную с дисперсностью системы в этом процессе:

(21.5)

Для этого надо вновь воспользоваться справочной термодинамической информацией и функциями для расчета величины ΔG₂ для определенной в опыте температуры второй остановки.