Решение задач
П
р и м е р 1. Вычислите
угловые коэффициенты касательных к
параболе
в точках
.
Решение.
Из геометрического смысла производной
(формула 1) угловой коэффициент касательной
.
Найдём
производную функции:
.
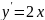Найдём значение производной в точке
.
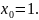
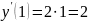Следовательно,
.
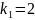Найдём значение производной в точке
.
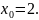
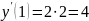Следовательно,
.
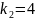П
р и м е р 2. У
параболы
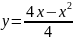проведены касательные в точках
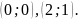Найдите углы наклона касательных к оси
Ох.
Решение.
По формуле (1)
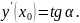
Найдём
.
.
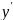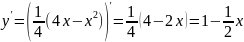Вычислим значение производной в точке
:
.
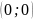Следовательно,
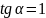и
.
Аналогично в точке
.
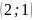
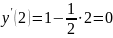Следовательно,
и
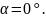
П
р и м е р 3.
В какой точке касательная к кривой
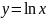наклонена к оси Ох
под
углом
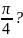
Решение. По формуле (1)
;
.
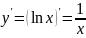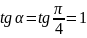Следовательно,
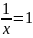и
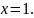
Подставив
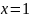в функцию
,
получим
.
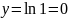Получили точку
.
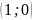П
р и м е р 4.
Составить уравнение касательной и
нормали к параболе
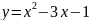в точке
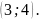
Решение. Уравнение касательной к кривой имеет вид .
Из
условия задачи
.
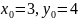Найдём производную
.
;
.
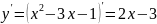Подставив
все значения в уравнение
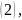получим уравнение касательной
или
.
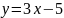Составим уравнение нормали, воспользовавшись формулой :
или
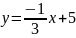
Вопросы для самопроверки
Дайте определение касательной к кривой.
Что называется нормалью к кривой?
В чём заключается геометрический смысл производной? Запишите формулу.
Запишите уравнение касательной к кривой в данной точке.
Запишите уравнение нормали к кривой в данной точке.
УПРАЖНЕНИЯ
Найти угловой коэффициент касательной, проведённой к кривой
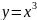
в
точке
.
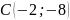Кривая задана уравнением
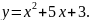Определить углы наклона касательных
к положительному направлению оси
,
проведённых к кривой в точках
с
абсциссами
.
В какой точке касательная к кривой
:
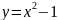а) параллельна оси
;
б) образует с осью
угол 45
?В какой точке касательная к графику функции
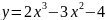параллельна оси абсцисс?Найти угол наклона касательной к кривой
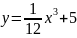в точке, абсцисса которой
равна 2.
Составить уравнение касательной к кривой
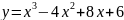в точке
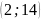.Найти касательную к кривой
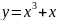в точке с абсциссой
.
Задачи для самостоятельного решения
8.
Найти абсциссу точки параболы
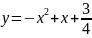, в которой касательная параллельна
оси абсцисс.
9.
Найти угловой коэффициент касательной,
проведённой к кривой
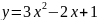
в
точке
.
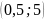10.
В какой точке касательная к кривой
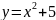образует с осью
угол 30
?
11.
Составить уравнение касательной к
параболе
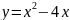в точке с абсциссой
12.
Составить уравнение касательной к
гиперболе
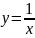в точке
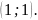
13. В каких точках угловой коэффициент касательной к кубической параболе
равен 3?
14.
Составить уравнение касательной к
параболе
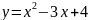в точке с абсциссой
.
15.
Составить уравнение касательной к
кривой
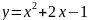в точке с абсциссой
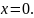
16.
Составить уравнение касательной к
кривой
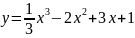в точке с абсциссой
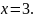
17.
Какой угол образует с осью абсцисс
касательная к параболе
,
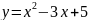проведённая в точке M
?
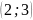Составить уравнение этой касательной.
18.
Найти координаты точки, в которой
касательная к параболе
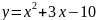образует с осью
угол
в 135
.
19.
На кривой
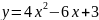найти точку, в которой касательная
параллельна прямой
.
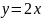20.
В какой точке касательная к графику
функции
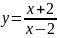образует угол 135
с осью ?