
- •Методическое пособие
- •Приложения производной
- •Содержание
- •Введение
- •Физический и механический смысл производной. Понятие второй производной
- •1. Физический смысл первой производной
- •2. Производная второго порядка. Производная n-го порядка.
- •3. Механический смысл второй производной.
- •Вопросы для самопроверки
- •Приложение производной к решению прикладных задач
- •Понятие касательной и нормали. Геометрический смысл производной
- •1. Понятие касательной и нормали к кривой
- •2. Геометрический смысл производной
- •Решение задач
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
- •Исследование функции на монотонность с помощью производной
- •Признаки возрастания и убывания функции.
- •Вопросы для самопроверки
- •Упражнения
- •Исследование функции на экстремум по первой и второй производной
- •Определение точек экстремума.
- •2. Признаки существования точек экстремума.
- •Второе правило исследования функции на экстремум.
- •Если то - точка максимума,
- •Вопросы для самопроверки
- •Упражнения
- •Задания для самостоятельного решения
- •Применение производной к исследованию функции на монотонность и экстремумы
- •Построение графика квадратного трёхчлена
- •Упражнения
- •Наибольшее и наименьшее значения функции на отрезке
- •1. Найти критические точки, принадлежащие отрезку и вычислить значения функции в этих точках.
- •2. Вычислить значения функции на концах отрезка , то есть найти и .
- •3. Из полученных значений функции выбрать наибольшее и наименьшее.
- •Упражнения
- •Задания для самостоятельного решения
- •Примерный вариант контрольной работы по теме
- •Литература
Вопросы для самопроверки
1. В чём заключается физический смысл первой производной?
2. Как найти мгновенную скорость прямолинейного неравномерного движения? Запишите формулу.
3. Что называется производной второго порядка, третьего порядка, n-го порядка?
4. В чём заключается механический смысл производной?
5. Как найти ускорение прямолинейного неравномерного движения в данный момент времени? Запишите формулу.
Приложение производной к решению прикладных задач
Решите задачи.
Путь, пройденный материальной точкой, задаётся уравнением
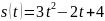 .
Найти скорость и ускорение точки в
конце 5-й секунды.
.
Найти скорость и ускорение точки в
конце 5-й секунды.
Вычислить ускорение материальной точки в конце 3-й секунды, если точка движется по закону
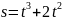 .
.Точка движется прямолинейно по закону
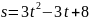 .
Найти скорость и ускорение точки в
момент
.
Найти скорость и ускорение точки в
момент
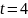 секунды.
секунды.Материальная точка движется прямолинейно по закону
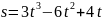 .
Найти её ускорение в конце 3-й секунды.
.
Найти её ускорение в конце 3-й секунды.Путь, пройденный клетью подъёмной машины, определяется уравнением
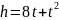 .
Найти скорость и ускорение в момент
времени 5 с.
.
Найти скорость и ускорение в момент
времени 5 с.
Определить момент , в который ускорение прямолинейного движения, совершаемого по закону
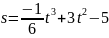 ,
равно нулю. Какова при этом скорость?
,
равно нулю. Какова при этом скорость?Закон движения частицы определяется уравнением
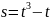 .
Каково ускорение частицы в момент,
когда её скорость равна 11 м/с?
.
Каково ускорение частицы в момент,
когда её скорость равна 11 м/с?Температура тела T изменяется в зависимости от времени t по закону
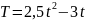
 .
С какой скоростью нагревается это тело
в момент времени
.
С какой скоростью нагревается это тело
в момент времени
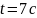 ?
?
Количество электричества, протекающего через проводник, задаётся формулой
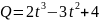 .
Найти силу тока в конце 4-й секунды.
.
Найти силу тока в конце 4-й секунды.Сила тока изменяется в зависимости от времени по закону
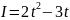 (I
– в амперах, t
– в секундах). Найти скорость изменения
силы тока в конце 8-й секунды.
(I
– в амперах, t
– в секундах). Найти скорость изменения
силы тока в конце 8-й секунды.Известно, что тело массой m = 5кг движется прямолинейно по закону
 .
Найдите кинетическую энергию тела
через
2с после начала движения.
.
Найдите кинетическую энергию тела
через
2с после начала движения.Две материальные точки движутся прямолинейно по законам:
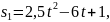
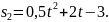 В какой момент времени скорости их
равны?
В какой момент времени скорости их
равны?Две материальные точки движутся прямолинейно по законам:
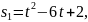
 В какой момент времени скорость первой
точки будет в два раза больше скорости
второй?
В какой момент времени скорость первой
точки будет в два раза больше скорости
второй?Основание а параллелограмма изменяется по закону
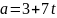 ,
а высота
,
а высота
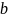 по
закону
по
закону
 Вычислите скорость изменения его
площади
Вычислите скорость изменения его
площади
 в
момент t
= 4c.
(Основание а
и
высота b
измеряются
в сантиметрах).
в
момент t
= 4c.
(Основание а
и
высота b
измеряются
в сантиметрах).Радиус круга R изменяется по закону
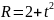 .
C
какой скоростью изменяется его площадь
в момент
.
C
какой скоростью изменяется его площадь
в момент
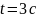 ,
если радиус круга измеряется в
сантиметрах.
,
если радиус круга измеряется в
сантиметрах.Материальная точка массой 2кг движется прямолинейно по закону
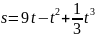 ,
где s-
путь в метрах, t
– время в секундах. Найдите силу,
действующую на неё в момент t
= 3 c.
,
где s-
путь в метрах, t
– время в секундах. Найдите силу,
действующую на неё в момент t
= 3 c.
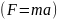
Маховик, задерживаемый тормозом, поворачивается за t секунд на
угол
(t)
=
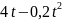 (рад).
Найдите:
(рад).
Найдите:
а) угловую скорость вращения маховика в момент t = 6с;
б) в какой момент маховик остановится?
Материальная точка движется прямолинейно по закону
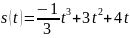 ,
,
где s – путь в метрах, t – время в секундах. Найдите:
а) момент времени t, когда ускорение точки равно 0;
б) скорость, с которой движется точка в этот момент времени.
