9. Теорема Гаусса-Маркова (формулировка, смысл условий и вывода).

Применение метода наименьших квадратов (МНК) к оценке параметров линейной модели не всегда позволяет получить состоятельные оценки (Напоминаю: состоятельные оценки - обладающие свойством несмещённости при больших объёмах выборки).

Для получения состоятельных оценок необходимо, чтобы они удовлетворяли ряду условий, эти условия сформулированы в теореме Гаусса-Маркова.

Теорема Гаусса-Маркова формулирует условия, при которых МНК позволяет получить наилучшие оценки параметров линейной модели множественной регрессии.

К.Ф Гаусс (1777-1855) – разработка МНК

А.А. Марков (1856-1922) – сформулировал условия, при которых МНК позволяет получить состоятельные оценки.

Сформулируем постановку задачи:

Имеем:

1) спецификацию модели в виде линейного уравнения множественной регрессии

 (« уравнение звёздочка» *)

2) выборку из n наблюдений

Значения переменных в каждом наблюдении связаны между собой по правилу (*)

Следовательно,

(5.17)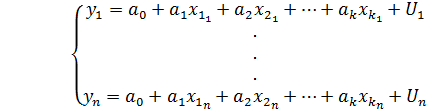 

Система уравнений (5.17) называется системой уравнений наблюдений или схемой Гаусса-Маркова.

В компактной (матричной) записи эта система имеет вид

В матрице Х в первом столбце единицы появляются только в тех случаях, когда спецификация содержит свободный параметр   .

Если этот параметр отсутствует, то и в матрице Х этот столбец отсутствует.

Перейдём к задаче.

Необходимо

1. найти значение состоятельных оценок параметров моделей

2. оценку ошибки случайного возмущения

3. оценку наилучшего прогноза с помощью модели (5.17)

4. оценку ошибки прогноза эндогенных переменных

Предпосылки теоремы Гаусса-Маркова следующие:

1) математическое ожидание случайных возмущений во всех наблюдениях равно нулю

 (5.20)

2) дисперсия случайных возмущений во всех наблюдениях одинакова и равна const . И свойство однородности случайных возмущений

 (5.21)

3) ковариация между парами случайных возмущений в наблюдениях равна нулю

 (5.22)

→ отсутствие автоковариации случайных возмущений

Неравенство нулю (≠0) есть автоковариация

4) ковариация между вектором-регрессором и вектором случайных возмущений равна нулю → регрессоры и случайные возмущения НЕ зависят друг от друга

 .

(далее непонятная неведомая фигня)

Если матрица X неколлинеарна, т.е нет ни одного столбца, который можно было бы приставить в виде линейной комбинации других столбцов, то

1) наилучшая оценка вектора параметров линейной модели множественной регрессии вычисляется по правилу

 =   (5.24) - она (оценка) соответствует МНК

2) значение несмещённых оценок параметров

Ковариационная матрица параметров модели вычисляется

 (5.25)

3) дисперсия случайного возмущения равна:

 (5.26)

4) наилучший прогноз по модели (5.17) в точке 

 +…+   (5.27)

5) оценка ошибки прогноза эндогенной переменной равна

10. Линейная модель множественной регрессии. Порядок её оценивания методом наименьших квадратов в Excel. Смысл выходной статистической информации функции линейн.

В этой модели две эндогенные переменные x1,х2 и одна экзогенная у. Случайное возмущение u предполагается гомоскедастичным. Спецификация содержит 4 параметра: а0,а1,а2, 

Получили линейную эконометрическую модель в виде изолированных уравнение с несколькими объясняющими переменными или модель линейной множественной регрессии. Экономический смысл коэфицентов а1,а2 функции регрессии модели : это ожидаемые предельные значения переменной у по объясняющим переменным соответственно х1 и х2.

Модель является базовой моделью эконометрики по той причине, что, во-первых, к такой модели может быть трансформирована практически любая эконометрическая модель в виде изолированного уравнения. Во-вторых, поведенческие уравнения в линейных моделях из одновременных уравнений имеют такой же вид. Эконометрическая модель Самуэльсона-Хикса является частным случаем модели. Рассмотренный нами порядок рассмотрения оценивания при помощи Excel модели сохраняются без какого-либо изменения при произвольном количестве К экзогенных переменных х1,х2,…,хК.

Мы располагаем информацией в виде конкретных значений экзогенных и эндогенных переменных модели.

Порядок оценивания модели состоит из след шагов:

Шаг 1. В столбце А листа Excel с первой строчки расположить значения эндогенной переменной у. В столбцах В и С, начиная с первой строчки, записать значения экзогенных переменных соответственно x_1t и x_2t.

Шаг 2. Активировать ячейку с адресом А(n+1) и на стандартной панели инструментов целкнуть мышью кнопку вставки ф-ии F_x.

Шаг 3. В появившемся окне выбрать функцию линейн.

Шаг 4. В строчке «неизвестные_значения_у» указать адрес А1:Аn диапазона значений эндогенной переменной y_t, а в строчке «известные_значения_х» адрес B1:Cn известных значений предопределенных переменных х1,х2.

Шаг 5. В строчку «Конст» диалогового окна занести цифру 1.

Шаг 6. В строчку «Статистика» диалогового окна занести цифру 1 и щелкнуть «Ок».

Шаг 7. Выделить мышью диапазон ячеек А(n+1):C(n+5).

Шаг 8. Щелкнуть мышью по строке формул.

Шаг 9. Нажать клавиши Ctrl+Shift+Enter.

В итоге в выделенном диапазоне ячеек появится результаты оценивания модели.

Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:

Значение коэффициента а2	Значение коэффициента а1	Значение коэффициента a0
Среднеквадратическое отклонение а2	Среднеквадратическое отклонение а1	Среднеквадратическое отклонение a0
Коэффициент детерминации R2	Среднеквадратическое отклонение у	Н/Д
F-статистика	Число степеней свободы	Н/Д
Регрессионная сумма квадратов	Остаточная сумма квадратов	Н/Д

Назначение фиктивных переменных. Может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровней. Это могут быть разного рода атрибутивные признаки. Чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены цифровые значения. Такого рода переменные принято называть фиктивными переменными.

Рассмотрим применение фиктивных переменных для функции спроса. Предположим, что по группе лиц мужского и женского пола изучается зависимость потребления кофе у от цены х. В общем виде уравнение регрессии имеет вид: y=a+b*x+ε. Отдельно для лиц муж пола: y1=a1+b1*x1+ε1. Для жен: y2=a2+b2*x2+ε2

Объединив эти уравнения и введя фиктивные переменные (например пол) получим следующее выражение: y=a1*z1+a2*z2+b*x+ε, где z1 и z2 фиктивные переменные.

В общем уравнении регрессии зависимая переменная у рассматривается как функция не только цены х, но и пола (z1, z2). Переменная z принимает всего два значения: 1 и 0. При этом когда z1 = 1, то z2 = 0 и, наоборот.

Случайные переменные (дискретные и непрерывные), их закон распределения и основные количественные характеристики. Выборочные значения основных количественных характеристик случайных величин и их оценивание.

Переменная величина x с множеством возможных значений Ax называется случайной, если ее возможные значения ti появляются в некотором опыте со случайными элементарными исходами ui вида: ui: x= ti, где ti. Переменная величина, все значения которой можно занумеровать, называется дискретной переменной. Если возможные значения переменной x непрерывно заполняют собой некий интервал (или объединение интервалов) числовой прямой, т.е. Ax есть интервал числовой прямой между некоторыми точками a и b, Ax =(a,b), то такая величина называется непрерывной.

Законом распределения СВ называется всякое соотношение, устанавливающее связь между возможными значениями СВ и соответствующими им вероятностями.

Для дискретной СВ закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически. Пример:

X:

x1	x2	…	xi	…	xn
p1	p2	…	pi	…	pn

или 

Такая таблица называется рядом распределения дискретной СВ.

Для любой дискретной величины

Если по оси абсцисс откладывать значения СВ, по оси ординат – соответствующие их вероятности, то получаемая (соединением точек) ломаная называется многоугольником или полигоном распределения вероятностей.

Две СВ называются независимыми, если закон распределения одной из них не меняется от того, какие возможные значения приняла другая величина.

Закон (ряд) распределения дискретной СВ даёт исчерпывающую информацию о ней, так как позволяет вычислить вероятности любых событий, связанных со СВ. Однако такой закон (ряд) распределения бывает трудно обозримым, не всегда удобным (и даже необходимым) для анализа.