§3. Числовые характеристики случайных величин.
Закон распределения полностью характеризует случайную величину. Однако при решении многих практических задач достаточно лишь знать лишь некоторые числовые параметры, характеризующие отдельные существенные свойства (черты) закона распределения СВ. такие числа принято называть числовыми характеристиками СВ.
Важнейшими из них являются характеристики положения: математическое ожидание (центр распределения СВ), характеристики рассеяния: дисперсия (отклонение значений СВ от ее центра), среднеквадратичное значение.
3.1. Математическое ожидание случайной величины.
Математическим ожиданием дискретной случайной величины называется сумма всех возможных произведений значений случайной величины на их вероятности:
.
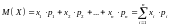Вероятностный смысл математического ожидания состоит в том, что оно является средним арифметическим СВ Х
Математическим ожиданием непрерывной случайной величины Х, с плотностью вероятности f(x) называется число
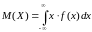
Свойства математического ожидания:
Если все значения случайной величины Х принадлежат промежутку [a; b], то математическое ожидание не может быть меньше a и больше b.
Математическое ожидание постоянной равно самой постоянной:
.
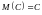Замечание:
Отклонением
случайной величины Х
от ее математического ожидания называется
разность между случайной величиной Х
и ее математическим ожиданием:
.
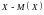Математическое ожидание отклонения случайной величины Х от ее математического ожидания равно нулю:
3.2. Дисперсия.
Только математическое ожидание не может в достаточной степени характеризовать СВ. Легко указать такие случайные величины, которые имеют одинаковые математические ожидания, но различные возможные значения, причем у одной из них возможные значения могут располагаться вблизи математического ожидания, а у другой – далеко.
Таким образом, зная лишь математическое ожидание случайной величины, еще нельзя судить ни о том, какие возможные значения она может принимать, ни о том, как они рассеяны вокруг математического ожидания. Поэтому в качестве характеристики, показывающей степень рассеяния значений случайной величины относительно центра, рассматривается дисперсия случайной величины.
Дисперсией (рассеянием) случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
для
ДСВ Х
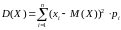
для
НСВ Х 
Н а практике вычисление дисперсии лучше производить по следующей формуле.
,
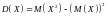где
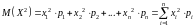
для дискретной случайной величины и
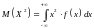
для непрерывной случайной величины.
Свойства дисперсии:
Дисперсия всегда неотрицательна:
.Дисперсия постоянной равна нулю:
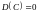.Дисперсия суммы случайной величины Х и постоянной величины равна дисперсии случайной величины Х:
.
3.3. Среднее квадратическое отклонение.
Недостатком дисперсии является то, что ее размерность равна размерности квадрата случайной величины, поэтому в ряде случаев для описания разброса используют среднеквадратическое отклонение, которое имеет ту же размерность, что и сама случайная величина.
Средним квадратическим отклонением σ(Х) называется арифметическое значение квадратного корня из ее дисперсии:
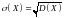
Пример 1: Имеется 10 студенческих групп, насчитывающих соответственно 12, 10, 15, 14, 10, 12, 9, 12, 14, 13. Установить закон распределения дискретной случайной величины Х, представляющей собой число студентов в наугад выбранной группе, построить многоугольник распределения и найти ее числовые характеристики.
X |
|
|
|
|
|
|
P |
|
|
|
|
|
|
Задача 2: Для функции распределения непрерывной случайной величины
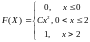
найти коэффициент С и определить вероятность попадания СВХ в интервал [0; 1]. Найти числовые характеристики этой функции