3.7. Метод замены переменной в неопределенном интеграле.

Преобразование интеграла производится по формуле

; . (1)

При этом предполагается, что функция непрерывна, а функция имеет непрерывную производную.

Примеры.

.

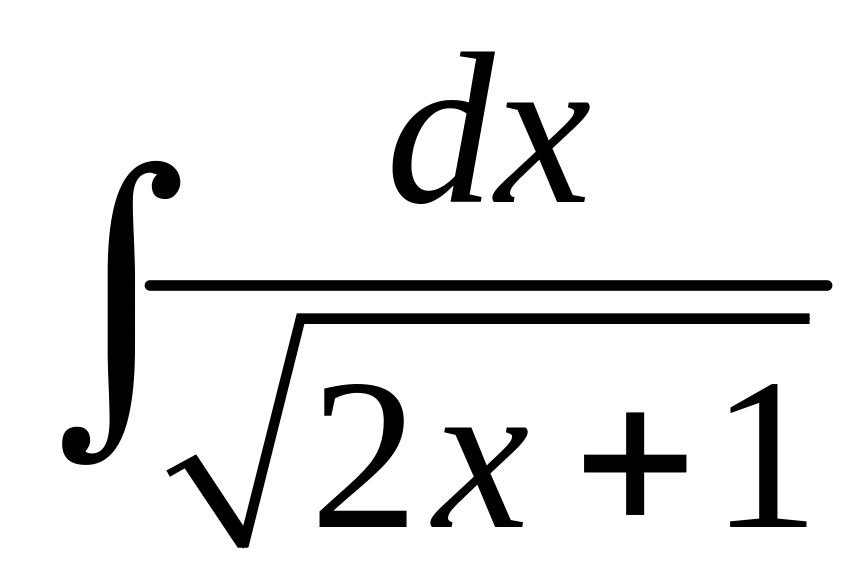Замена переменной или по формуле (1) преобразует данный интеграл к виду

.

.

= =2y-2 +c=2(1+ )–2 )+c.

3.8. Метод интегрирования подстановкой.

1. Интегралы , где R - рациональная функция; целые числа, которые вычисляются с помощью подстановки ; s - общий знаменатель дробей

Пример. Найдите неопределённый интеграл .

Выполняем подстановку: х + 1 = t⁴

2. К интегралам от функций, рационально зависящих от тригонометрических функций, сводятся интегралы:

подстановкой x=asint;

- подстановкой x=atgx;

- подстановкой x=a sec t.

3. Подстановка Эйлера преобразует интеграл .

к виду .

4. Интеграл 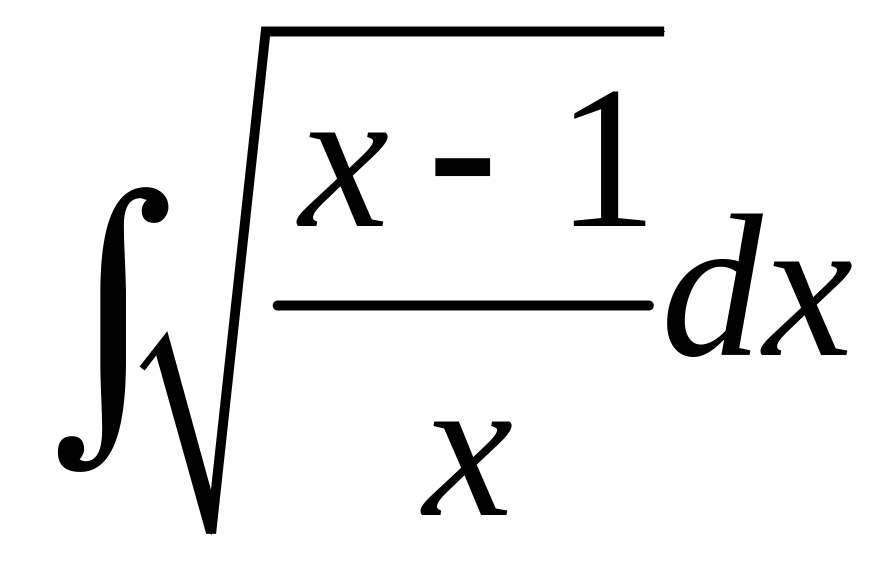приводится к интегралу от рациональной функции подстановкой , в результате которой получает вид

При вычислении интеграла от рациональной функции использован метод интегрирования по частям при .

5. Интеграл от биномиального дифференциала , где и – целые, а и – рациональные числа, приводится с помощью подстановки Чебышева к интегралу от рациональной функции в следующих случаях:

1. – целое число (подстановка );

2. – целое число (подстановка );

3. – целое число (подстановка ).

В других случаях интеграл от биномиального дифференциала не выражается в конечном виде через элементарные функции.

Пример. Найдите неопределённый интеграл

Здесь Пусть откуда дифференцированием находим Тогда

6. Подстановка или преобразует интеграл к виду

Определенный интеграл. Свойства определенного интеграла. Формула Ньютона – Лейбница.

Криволинейной трапецией называют фигуру в плоскости , ограниченную прямыми , , графиком функции и осью . Поставим задачу вычисления площади криволинейной трапеции. Приближенной решение задачи можно получить следующим образом. Разобьем отрезок на интервалов точками . На каждом интервале выбираем точку и строим составную фигуру из прямоугольников, показанную на рис. 1. По интуитивным представлениям, площадь ступенчатой фигуры приближенно совпадает с площадью криволинейной трапеции, откуда получаем формулу

.

Рис. 1

Чем больше , тем лучше приближение. Точное равенство получается в пределе при :

.

Предел суммы в правой части равенства называют определенным интегралом от функции в пределах от до и обозначают . Таким образом, независимо от геометрического смысла, определение определенного интеграла будет

. (3)

доказывается, что предел в правой части выражения (3) существует для любой функции , непрерывной на интервале и не зависит от расположения точек и .

Необходимость специального рассмотрения пределов вида (3) вызвана тем, что такие пределы встречаются во многих задачах, в том числе в задачах прикладного характера. Сходство обозначений определенного и неопределенного интегралов не случайно и будет выяснено в дальнейшем.

Теорема. Если функция непрерывна на отрезке , то функция дифференцируема в любой внутренней точке этого отрезка, причем .

Другим следствием доказанной теоремы является формула Ньютона - Лейбница:

если функция непрерывна на интервале , то

, (4)

где – первообразная функции .

Формула Ньютона - Лейбница устанавливает связь между неопределенным и определенным интегралом и дает мощное средство вычисления определенных интегралов. Например, функция имеет первообразную (находим ее из неопределенного интеграла) и поэтому .

При применении формулы Ньютона - Лейбница следует проверять подынтегральную функцию на непрерывность в интервале интегрирования. В противном случае возможен неверный результат. Например, результат вычисления интеграла неверен по причине разрыва функции в точке .