§ 4.3 «Радиальное уравнение» и волновые функции
4.3.1 Анализ радиального уравнения
Уравнение (4.1) при n =1 и ℓ = 0 имеет вид:
-
[
+
] – (ℇ1
+ k
)
= 0, (4.3)
Где обозначено ℜ10
Решением может быть простая экспонента, поскольку при r →0 второе и четвёртое слагаемые стремятся к нулю.
= A1 exp[- ( r/ao)]
Ур. (4.3) станет тождеством, если:
ao
=
-
т.н. боровский радиус,
ℇ1=
-
= -
-
энергия основного уровня электрона.
→0 при r →0 и не имеет узлов.
С другой стороны в классическом понимании движение здесь – качание маятника относительно силового центра. Необычный результат.
4.3.2 Волновые функции состояний (орбитали)
Для n =2, ℓ =0
=
A2
(1-
r/2ao)
exp[-
(
r/2ao)]
Эта функция уже имеет один узел.
При
ℓ
0
появляется угловая зависимость.
Так, при n = 2 и ℓ = 1, mℓ = 0 выражениe для орбитали таково:
=
A2,1
·(r/ao)
exp[-
(
r/2ao)]·
cos θ
При
n
= 2 и ℓ
=
1,
mℓ
=
следующие
орбитали:
=
A2,1,1
·(r/ao)
exp[-
(
r/2ao)]·
sin θ ·
Число узлов по радиусу остаётся прежним, но возникает один узел по углу.
Вероятность обнаружения электрона даётся выражением
dw = │ψ│2 4 r2 ·dr
См. на рис. изменения вероятности с расстоянием.
§ 4.4 Многоэлектронные атомы
4.4.1 Общие особенности
Качественные рассуждения уже могут дать полезные выводы.
Заметим, что:
а) Только два электрона могут описываться одной орбиталью, чтобы удовлетворялся принцип Паули;
б) электроны-соседи влияют друг на друга; имеет место экранирования ядра.
В последнем случае вводится эфф. заряд ядра Zeff . Z
Водород (Z =1)
Единственный электрон в состоянии 1s, потенциал ионизации 13,6 эВ, наличие спина мало сказывается в первом приближении. Тонкая структура возбуждённых уровней обуславливается взаимодействием собственных магнитных спинового и орбитального моментов (появятся дублеты).
Гелий (Z =2)
В случае одного электрона, т.е. для иона, «работает» модель водороподобного атома
Энергия ионизации
ℇи
= -
=13,6 ·
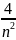= 54 эВ,
что близко к опытным данным.
В атоме гелия электроны как бы видят ядро с зарядом Z* Zeff = Z - σ , где
σ = у них одинаковая орбиталь, волновая функция при n = 2 имеет один узел.
Оболочка из двух электронов замкнутая.
Литий (Z =3)
Эффективный заряд σ = 1,25. Третий электрон относительно слабо связан с ядром, его называют валентным. Его основное состояние 2s. Все состояния с одинаковыми n и ℓ называются подоболочкой. Третий электрон попадает в p - состояние.В принципе, в р – состоянии может находится 2(2ℓ +1)= 6 электронов. Их общее число в оболочке n =2 не более
2 +6 = 8.
Список можно продолжить. Картина будет усложняться, а главное необходимо вводить квантовые числа для атомной системы с большим числом электронов.
4.3.2 Диаграммы переходов и правила отбора
Важно, что при излучении (поглощении),связанном с квантовыми переходами, долен выполняться закон сохранения импульса наряду с законом сохр. энергии.
Правила отбора состоят в том, что переходы разрешены при
ℓ = 1
В многоэлектронных атомах также
L = 1 и S =0. Значения суммарного момента импульса J изменяются на единицу: J = 1, переходы между состояниями с J = 0 запрещены. Есть особые отклонения, их детализировать сйчас не будем.
ψ(r,t)
f
fn
x
(
)I│l-0
=(
)II│l+0
│ψ│2
d 3r = 1 L L L m ℏ2ℓ(ℓ+1)
υ2
=
υг
=
φ
= (2m
+1)
π
φ
= 2πm
ħω
ħω
hν
ħ
ħ
ψn ψ*n
П
ψ(x,t)
j
ħ
-
ψ
→
ω →
= υ2
δ
=
ωo2
=
cos
Σ
α
φ
q
φo
β
ω ωо
2 π
ψ (x,t)
x
k
§
ℓ δ λ φ ε θ α π υ ν ω τ μ ψ ρ
∙
§ ΄
Мz
γ σ ℓ
→ ∶ § π tg φ ψ → ω → t μ μо εoε ∠
δ = ωo2 = cos(ωt + φo) sin (ωt + φo) sin2
е-
δt
ω
=
εm
рез
Cambria Math (буквеподобные
сим.)
ħ const