2.3. Расчет переходных процессов

Краткие теоретические сведения. При учете только механической инерционности привода законы изменения скорости и момента M определяются из решения уравнения движения его механической части

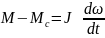, (3)

при заданных начальных условиях и виде зависимостей M(и M_с(где J_ – суммарный момент инерции подвижных частей привода

Если в простейшем случае в переходном процессе амплитуда и частота напряжения на статоре асинхронного двигателя неизменны и, кроме того, можно принять M(const,  M_с(const, решение (3) относительно скорости имеет вид

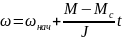(4)

где – начальное значение скорости в переходном процессе.

При линейном законе изменения M(и M_с(const решения (3) для скорости и момента имеют одинаковый вид

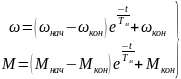(5)

где 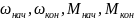– начальные и конечные значения скорости и момента в переходном процессе, Т_м – электромеханическая постоянная времени.

При плавном по линейному закону изменении амплитуды и частоты напряжения на статоре двигателя и при условии, что на рабочем участке механических характеристик они могут быть приняты линейными, решение уравнения (3) для скорости приобретает вид

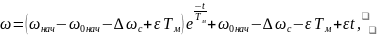(6)

где 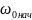– начальное значение скорости идеального холостого хода двигателя в переходном процессе; 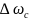– статический перепад скорости под действием нагрузки; 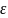– темп изменения скорости идеального холостого хода двигателя в переходном процессе (имеет размерность углового ускорения).

Уравнение для момента в данном случае получаем в результате дифференцирования по времени уравнения (6), подстановки полученного результата в уравнение (3) и решения его относительно момента.

Анализ нагрузочной диаграммы и тахограммы движения механизма в примере показывает, что его рабочий цикл включает следующие переходные процессы:

а) пуск с ограничением пускового тока;

б) увеличение скорости;

в) наброс нагрузки;

г) торможение.

а) Пуск. Поскольку при плавном изменении выходных параметров преобразователя частоты ток двигателя с некоторым допущением можно считать пропорциональным моменту, требование уменьшения пускового тока двигателя влечет за собой изменение пускового момента М_n. Учитывая, что

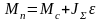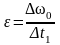и , а также 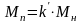, находим

где ₀ - изменение скорости идеального холостого хода двигателя в переходном процессе.

В нашем случае ₀=_01p, поэтому

t`₁=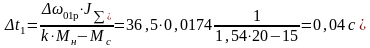

где ; .

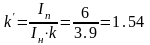Следовательно, в процессе пуска привода выходные параметры преобразователя частоты должны плавно нарастать по линейному закону в течение времени t'=0,04 с.

Процесс пуска в данном случае состоит из нескольких этапов.

Первый этап – задержка по времени в нарастании скорости на величину t₃, необходимая для увеличения момента двигателя от 0 до М_с1:

,

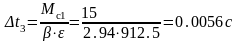где ; ; .

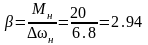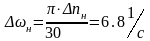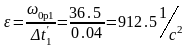При этом момент двигателя нарастает по линейному закону от 0 до М_с1 согласно уравнению

(7)

Следует обратить внимание на то, что при пуске вхолостую или при изменении скорости под нагрузкой относительно некоторого начального ненулевого её значения в начале переходного процесса момент двигателя равен моменту нагрузки, поэтому этот этап в переходном процессе отсутствует.

На втором этапе пуска, которому соответствует линейно нарастающий участок заданной тахограммы движения, уравнение для скорости получаем из уравнения (6) при подстановке туда =0, ,

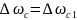
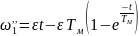, (8)

где

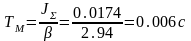
Уравнение для момента получаем в результате дифференцирования по времени уравнения (8) и подстановки полученного результата в уравнение (3). Опуская промежуточные преобразования, приходим к уравнению для момента двигателя на этом этапе в виде

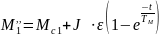(9)

Длительность второго этапа

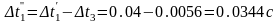
К концу второго этапа скорость двигателя достигает величины ,

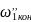значение которой определяют из уравнения (8) при подстановке в него :

.

Согласно (9) момент двигателя при

На третьем этапе скорость и момент двигателя изменяются по экспоненциальным законам согласно уравнениям (5). В соответствии с принятыми обозначениями переменных для этого этапа приходим к уравнениям

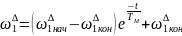(10)

, (11)

где ; ;

;

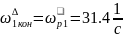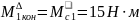
Временные диаграммы изменения скорости и момента двигателя для пуска изображены на рис. 3.

б) Увеличение скорости. В данном случае точка, отображающая состояние привода, мгновенно переходит из положения 1 на характеристике (б) (см. рис. 2) в положение 2 характеристики (в), и в дальнейшем скорость и момент в переходном процессе изменяются в соответствии с участком 2-3 характеристики (в).

Расчет с использованием усредненной механической характеристики двигателя в переходном процессе.

Заменив реальную нелинейную механическую характеристику двигателя на участке, соответствующем переходному процессу, усредненной зависимостью (штрихпунктирная линия на рис. 2) и определив средний момент на этом участке М_ср2 =41 Нм, найдем время переходного процесса:

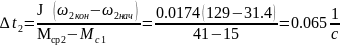
где ; .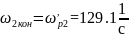

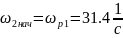При допущении о постоянстве момента двигателя в переходном процессе можно записать приближенное уравнение для его скорости в интервале времени t₂ в виде

(8)

Временные диаграммы изменения скорости и момента двигателя для этого случая изображены на рис. 4 (сплошные линии).

Расчет с использованием реальной нелинейной механической характеристики двигателя.

Наиболее общим подходом к расчету переходных процессов в электроприводе при заданных зависимостях M() и M_c() без ограничения их вида является использование приближенного численного или графо-аналитического решения уравнения движения электропривода. Для этого разбиваем ось ординат на графике рис. 5 между точками 1 и 3 на достаточно малые равные интервалы  так, чтобы в пределах каждого из интервалов без существенной погрешности можно было принять M = const. Для определенности предположим, что это условие выполняется при

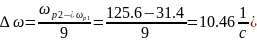
Тогда в уравнении движения можно производную заменить отношением приращений 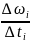и записать

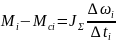(9)

где t_i – длительность переходного процесса на i – том интервале. Значение t_i для i – ого интервала определяем из (9) как

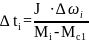(10)

Далее из графиков на рис. 5 для каждого i – того интервала последовательно берутся численные значения M_i и M_c и подставляются в формулу (10), из которой получают численные значенияt_i.

Результаты расчетов для интервалов ₁, ₂, …, ₉ сводим в таблицу 5.

Таблица 5

i	1	2	3	4	5	6	7	8	9
Mi	33.5	35.2	37.0	40	42.0	45.2	47.3	47.3	32.0
ti	0.0098	0.009	0.0084	0.0073	0.0067	0.00601	0.00562	0.00562	0.0106
t4	0.0098	0.0198	0.0272	0.0354	0.0412	0.0472	0.05283	0.05845	0.069

Затем в осях (t) отмечаются точки с координатами (t_i-1+ t_i), _i-1+ _), соединив которые плавной кривой получают график t). Зависимость M(t) строится также по точкам с использованием полученной ранее зависимости t) и известной кривой M(Вид получаемых при этом кривых показан на рис. 6.6,б. Наиболее эффективен изложенный подход к расчету переходных процессов при его компьютерной реализации.

Временные диаграммы изменения скорости и момента двигателя для этого случая изображены на рис. 4 (пунктирные линии).

в) При набросе нагрузки скорость и момент двигателя изменяются по экспоненциальным законам согласно уравнениям в общем виде (7). При этом точка, отображающая состояние привода, переходит из положения 3 (см. рис. 2) в положение 4 на характеристике (в). В соответствии с принятыми обозначениями для этого переходного процесса из (7) получаем уравнения

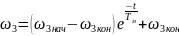; (9)

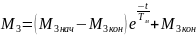_, (10)

где; ;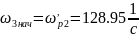

;

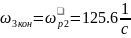
г) Торможение. Механическая характеристика асинхронного двигателя согласно условию будет представлять собой прямую, параллельную оси скоростей и отстоящую от нее на –М_п (прямая (г) на рис. 2).

Точка, отображающая состояние привода, мгновенно перейдет из положения 4 на характеристике (в) в положение 5 на характеристике (г), и дальнейшее изменение скорости и момента двигателя в переходном процессе будет отражаться участком 5-6 характеристики (г) на рис. 2.

Время торможения

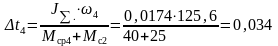с,

где ; .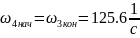

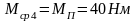Приближенное уравнение для скорости в интервале времени t₄ :

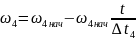
Временные диаграммы изменения скорости и момента двигателя для наброса нагрузки изображены на рис. 6., торможения - на рис. 7.