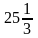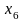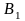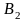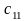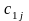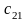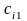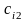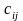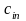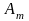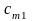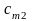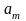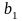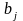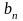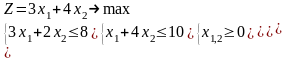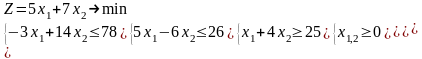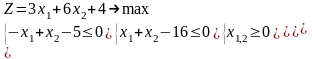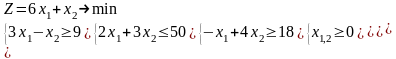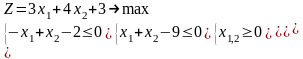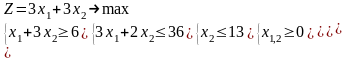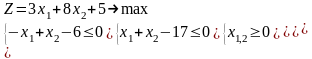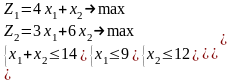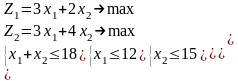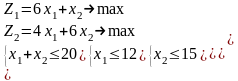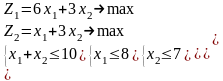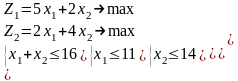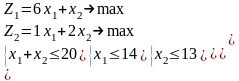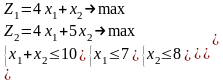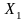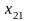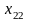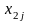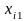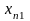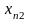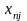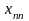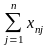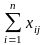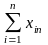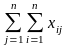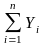- •Е.С. Филонова линейные модели в экономике Учебное пособие
- •Орел 2016
- •Рецензент:
- •Орлова и.В.
- •Содержание
- •Предисловие
- •Введение. Понятие, роль и этапы математического моделирования в экономике и финансах
- •Раздел1. Основы линейного программирования
- •1.1. Экономико-математическая модель оптимизационной задачи и задачи линейного программирования
- •1.2. Графический метод решения задачи линейного программирования
- •1.3. Симплекс-метод решения задач линейного программирования
- •1.4. Основы теории двойственности
- •Задачи для самостоятельного решения
- •Раздел 2. Специальные задачи линейного программирования
- •2.1. Задачи дискретного программирования
- •2.2.Транспортная задача. Методы построения опорного плана. Улучшение плана методом потенциалов
- •2 Этап.Построение системы потенциалов и проверка начального плана на оптимальность
- •Задачи для самостоятельного решения
- •Раздел 3. Задачи многокритериальной оптимизации
- •3.1. Происхождение и постановка задачи многокритериальной оптимизации
- •3.2. Основные методы решения многокритериальных задач
- •Задачи для самостоятельного решения
- •Раздел 4. Неотрицательные матрицы и модели Леонтьева
- •4.1. Некоторые сведения из линейной алгебры Собственные значения и собственные векторы неотрицательных матриц
- •Теорема Фробениуса – Перрона. Число и вектор Фробениуса, их свойства
- •4.2. Модель Леонтьева6 многоотраслевой экономики
- •Задачи для самостоятельного решения
- •Рекомендуемая литература
- •Е.С. Филонова линейные модели в экономике Учебное пособие
- •7,75Усл. Печ. Л. Тираж 500 экз. Заказ № 225
оценить целесообразность включения в план изделия четвертого вида ценой 70ед., на изготовление которого расходуется по две единицы каждого вида ресурсов.
4.6. На основании информации, приведенной в таблице, решается задача оптимального использования ресурсов на максимум выручки от реализации готовой продукции.
Вид сырья
|
Нормы расхода сырья на ед. продукции |
Запасы сырья |
||
А |
Б |
В |
||
I II III |
18 6 5 |
15 4 3 |
12 8 3 |
360 192 180 |
Цена изделия |
9 |
10 |
16 |
|
Требуется:
Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.
Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
Пояснить нулевые значения переменных в оптимальном плане.
На основе свойств двойственных оценок и теорем двойственности:
проанализировать использование ресурсов в оптимальном плане исходной задачи;
определить, как изменятся выручка от реализации продукции и план ее выпуска, если запас сырья I вида увеличить на 45кг, а II - уменьшить на 9кг;
оценить целесообразность включения в план изделия "Г" ценой 11ед., на изготовление которого расходуется 9, 4 и 6кг соответствующего вида сырья.
4.7. Предприятие выпускает четыре вида продукции и использует три вида оборудования: токарное, фрезерное, шлифовальное. Общий фонд рабочего времени оборудования каждого вида, нормы расхода и цены реализации единицы каждого вида продукции приведены в таблице.
Тип оборудования |
Нормы расхода ресурса на одно изделие |
Фонд рабочего времени,ч |
||||
А |
Б |
В |
Г |
|||
Токарное Фрезерное Шлифовальное |
2 1 1 |
1 0 2 |
1 2 1 |
3 1 0 |
300 70 340 |
|
Цена изделия |
8 |
3 |
2 |
1 |
|
|
Требуется:
Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.
Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
Пояснить нулевые значения переменных в оптимальном плане.
На основе свойств двойственных оценок и теорем двойственности:
проанализировать использование ресурсов в оптимальном плане исходной задачи;
определить, как изменятся выручка и план выпуска продукции, если фонд рабочего времени шлифовального оборудования увеличить на 24 часа;
оценить целесообразность включения в план изделия "Д" ценой 11ед., если нормы затрат оборудования 8,2 и 2ед. соответственно.
4.8. На основании информации, приведенной в таблице, решается задача оптимального использования ресурсов на максимум выручки от реализации готовой продукции.
Тип сырья |
Нормы расхода сырья на ед. продукции |
Запасы сырья |
||
Iвид |
IIвид |
IIIвид |
||
I II III |
1 3 1 |
2 0 4 |
1 2 0 |
430 460 420 |
Цена изделия |
3 |
2 |
5 |
|
Требуется:
Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.
Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
Пояснить нулевые значения переменных в оптимальном плане.
На основе свойств двойственных оценок и теорем двойственности:
проанализировать использование ресурсов в оптимальном плане исходной задачи;
определить, как изменятся выручка от реализации продукции и план ее выпуска, если запас сырья I вида увеличить на 10ед., а II - уменьшить на 80ед;
оценить целесообразность включения в план изделия четвертого вида ценой 7у.е., если нормы затрат сырья 2, 4 и 3ед.
4.9. Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цены реализации единицы каждого вида продукции приведены в таблице.
Тип сырья
|
Нормы расхода сырья на одно изделие |
Запасы сырья |
|||
А |
Б |
В |
Г |
||
I II III |
2 1 3 |
1 5 0 |
0,5 3 6 |
4 0 1 |
2400 1200 3000 |
Цена изделия |
7,5 |
3 |
6 |
12 |
|
Требуется:
Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.
Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
Пояснить нулевые значения переменных в оптимальном плане.
На основе свойств двойственных оценок и теорем двойственности:
проанализировать использование ресурсов в оптимальном плане исходной задачи;
определить, как изменятся выручка и план выпуска продукции при увеличении запасов сырья I вида на 100ед. и уменьшении на 150ед. запасов сырья II вида;
оценить целесообразность включения в план изделия "Д" ценой 10ед., если нормы затрат сырья 2, 4 и 3ед.
4.10. Для изготовления трех видов продукции используют четыре вида ресурсов. Запасы ресурсов, нормы расхода и цены реализации единицы каждого вида продукции приведены в таблице.
Вид ресурсов |
Нормы расхода ресурсов на ед. продукции |
Запасы ресурсов |
||
Iвид |
IIвид |
IIIвид |
||
Труд Сырье 1 Сырье 2 Оборудование |
3 20 10 0 |
6 15 15 3 |
4 20 20 5 |
2000 15000 7400 1500 |
Цена изделия |
6 |
10 |
9 |
|
Требуется:
Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.
Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности.
Пояснить нулевые значения переменных в оптимальном плане.
На основе свойств двойственных оценок и теорем двойственности:
проанализировать использование ресурсов в оптимальном плане исходной задачи;
определить, как изменятся выручка и план выпуска продукции при увеличении запаса ресурса первого вида на 24ед.;
оценить целесообразность включения в план изделия четвертого вида ценой 11ед., если нормы затрат ресурсов 8, 4, 20 и 6ед.
Раздел 2. Специальные задачи линейного программирования
Наряду с обычными задачами линейного программирования рассматривают некоторые специальные их виды: задачи дискретного программирования, транспортные задачи, задачи о назначениях.
2.1. Задачи дискретного программирования
В ряде задач линейного программирования вводятся ограничения на искомые переменные, например, ограничения на их непрерывность. К задачам дискретного программирования относят задачи с целочисленными или двоичными переменными, а также задачи, в которых переменные могут принимать значения из определенного промежутка.
Задачи оптимизации, в результате решения которых искомые значения переменных должны быть целыми числами, называются задачами (моделями) целочисленного программирования.
По смыслу значительной части экономических задач, относящихся к задачам линейного программирования, компоненты решения должны выражаться в целых числах, т.е. быть целочисленными. К ним относятся, например, задачи о производстве неделимой продукции (мебели, одежды, техники и т.д.).
Модель задачи целочисленного программирования отличается от модели обычной задачи лишь условием целочисленности:

Добавление условия целочисленностик обычной ЗЛП существенно усложняет ее решение. Для решения целочисленных задач используется ряд методов. Самый простой из них – округление полученных дробных значений переменных до ближайших целых чисел. Этот метод может привести к далекому от оптимального целочисленному решению, поэтому используют специально разработанные методы.
Все методы целочисленной оптимизации можно разделить на три основные группы:
Методы отсечения
Комбинаторные методы
Приближенные методы
Остановимся подробнее на методах отсечения. Сущность их состоит в том, что сначала задача решается без условия целочисленности. Если полученное оптимальное решение содержит дробные значения, то к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами:
- оно должно быть линейным;
- должно отсекать найденный оптимальный нецелочисленный план;
- не должно отсекать ни одного целочисленного плана.
Далее задача решается с учетом нового ограничения (правильного отсечения). После этого в случае необходимости добавляется еще одно ограничение и т.д.
Геометрически добавление каждого линейного ограничения отвечает проведению прямой, которая отсекает от многоугольника решений некоторую его часть вместе с оптимальной точкой с нецелыми координатами, но не затрагивает ни одной из целых точек этого многогранника (рис. 1).
На рисунке 1 ОКLM – область допустимых решений задачи, ограниченная прямыми (1), (2), (3) и осями координат; L – точка оптимального, но нецелочисленного решения задачи; (4) – прямая, отсекающая это нецелочисленное решение; OKNM – область допустимых решений расширенной задачи с новым ограничением; N – точка оптимального целочисленного решения.
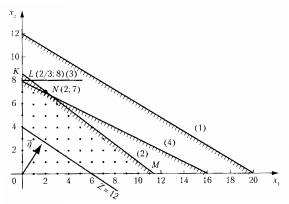
Рис. 1. Графическая иллюстрация метода отсечения
Один из алгоритмов решения задачи линейного целочисленного программирования методом отсечения, предложенный Р. Гомори, основан на симплексном методе3 и использует достаточно простой способ построения правильного отсечения.
Если
в оптимальном плане задачи переменная
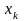 ,
по условию целочисленная, принимает
дробное значение, то к системе ограничений
добавляют неравенство
,
по условию целочисленная, принимает
дробное значение, то к системе ограничений
добавляют неравенство
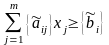 , (1)
, (1)
где
 обозначает дробную часть числа а,
а числа
обозначает дробную часть числа а,
а числа
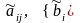 взяты из последней симплекс-таблицы из
строки, содержащей переменную
,
как базисную.
взяты из последней симплекс-таблицы из
строки, содержащей переменную
,
как базисную.
Если же дробные значения принимают несколько переменных, то дополнительное неравенство определяется числом с наибольшей дробной частью.
Замечание.
Под
дробной частью некоторого числаа
понимается наименьшее неотрицательное
число b
такое, что разность а
и bесть
целое, например,
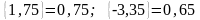 ,
т.к. -3,35-0,65=-4 – целое число.
,
т.к. -3,35-0,65=-4 – целое число.
Добавив, дополнительное ограничение в симплекс-таблицу, процесс вычислений повторяют. Проводя конечное число итераций, либо получают оптимальный план задачи целочисленного программирования, либо устанавливают ее неразрешимость.
Пример. Для приобретения оборудования по сортировке зерна фермер выделяет 34 ден. ед. Оборудование должно быть размещено на площади, не превышающей 60 кв. м. Фермер может заказать оборудование двух видов: менее мощные машины типа А стоимостью 3 ден. ед., требующие производственную площадь 3 кв. м, и производительностью за смену 2 т зерна, и более мощные машины типа В стоимостью 4 ден. ед., занимающие площадь 5 кв. м, и производительностью за смену 3 т сортового зерна.
Требуется составить оптимальный план приобретения оборудования, обеспечивающий максимальную общую производительность при условии, что фермер может приобрести не более 8 машин типа В.
Решение.
Обозначим
через
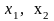 количество машин соответственно типа
А и В, через Z
– общую производительность.
количество машин соответственно типа
А и В, через Z
– общую производительность.
ЭММ задачи:
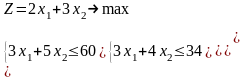
Приведем модель задачи к каноническому виду:
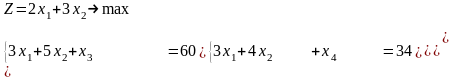 (2)
(2)
Решаем задачу симплексным методом. Графическая иллюстрация решения представлена на рисунке 1.
Первая симплексная таблица:
Базис |
Свободный член |
Переменные |
Оценочные отношения |
||||
|
|
|
|
|
|||
|
60 |
3 |
5 |
1 |
0 |
0 |
12 |
|
34 |
3 |
4 |
0 |
1 |
0 |
|
|
8 |
0 |
1 |
0 |
0 |
1 |
8 |
Z |
0 |
-2 |
-3 |
0 |
0 |
0 |
|
Вторая симплексная таблица:
Базис |
Свободный член |
Переменные |
Оценочные отношения |
||||
|
|
|
|
|
|||
|
20 |
3 |
0 |
1 |
0 |
-5 |
20/3 |
|
2 |
3 |
0 |
0 |
1 |
-4 |
2/3 |
|
8 |
0 |
1 |
0 |
0 |
1 |
|
Z |
24 |
-2 |
0 |
0 |
0 |
3 |
|
Третья симплексная таблица:
Базис |
Свободный член |
Переменные |
Оценочные отношения |
||||
|
|
|
|
|
|||
|
18 |
0 |
0 |
1 |
-1 |
-1 |
|
|
2/3 |
1 |
0 |
0 |
1/3 |
-4/3 |
|
|
8 |
0 |
1 |
0 |
0 |
1 |
|
Z |
|
0 |
0 |
0 |
2/3 |
1/3 |
|
Получили оптимальное решение:
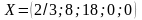 ;
;
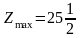 ,
,
которое не является целочисленным.
Дробное значение в оптимальном плане имеет переменная . Поэтому, используя соответствующую строку (вторую) в последней симплекс-таблице, получаем:
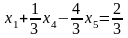 .
.
В соответствии с (1) к системе ограничений добавляем неравенство
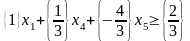 ,
,
или,
учитывая, что
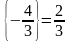 ,
т.к.
,
т.к.
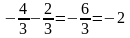 – целое, получим
– целое, получим
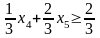 .
.
Вводим балансовую переменную :
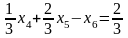
или, после деления на (-1), чтобы коэффициент при стал равен 1, получим:
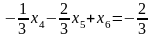 .
.
Включим в систему ограничений (в последнюю симплекс-таблицу) новую балансовую переменную в качестве основной переменной:
Базис |
Свободный член |
Переменные |
Оценочные отношения |
||||||
|
|
|
|
|
|
|
|||
|
18 |
0 |
0 |
1 |
-1 |
-1 |
0 |
|
|
|
2/3 |
1 |
0 |
0 |
1/3 |
-4/3 |
0 |
|
|
|
8 |
0 |
1 |
0 |
0 |
1 |
0 |
|
|
|
-2/3 |
0 |
0 |
0 |
-1/3 |
-2/3 |
1 |
|
|
Z |
|
0 |
0 |
0 |
2/3 |
1/3 |
0 |
|
|
Видим,
что полученное базисное решение
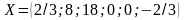 – недопустимо.
– недопустимо.
Замечание. После включения в систему ограничений дополнительного уравнения, соответствующего правильному отсечению, всегда будет получаться недопустимое базисное решение (т.к. знак в неравенстве (1) « » и дополнительную переменную необходимо вычитать).
Для
получения допустимого базисного решения
необходимо перевести в основные
переменную, входящую с положительным
коэффициентом в уравнение отсечения
,
в нашем случае это
или
 .
.
Выберем в качестве основной переменной, например, . В правильном отсечении
разделим все на 2/3, чтобы коэффициент при переменной стал равен 1:
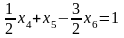 .
.
Заметим, что на этом этапе линейная функция не рассматривается, т.е. выбор переменной, которая будет переведена в следующей таблице в основные не осуществляется с помощью элементов последней строки (тем более, что там нет отрицательных значений).
Пересчет элементов следующей таблицы осуществляем обычным для симплекс-метода способом:
Базис |
Свободный член |
Переменные |
Оценочные отношения |
||||||
|
|
|
|
|
|
|
|||
|
19 |
0 |
0 |
1 |
-1/2 |
0 |
-3/2 |
|
|
|
2 |
1 |
0 |
0 |
1 |
0 |
-2 |
|
|
|
7 |
0 |
1 |
0 |
-1/2 |
0 |
3/2 |
|
|
|
1 |
0 |
0 |
0 |
1/2 |
1 |
-3/2 |
|
|
Z |
25 |
0 |
0 |
0 |
1/2 |
0 |
1/2 |
|
|
Заметим, что в строке переменной получились именно те коэффициенты и свободный член, которые имеют место в правильном отсечении
.
В последней строке нет отрицательных значений. В результате, в столбце «Свободный член», получаем целочисленное оптимальное решение:
X=(2, 7, 19, 0, 1, 0); Z=25.
Экономический смысл полученного решения:
максимальную производительность 25 т сортового зерна за смену можно получить приобретением 2 машин типа А и 7 машин типа В; при этом незанятая площадь помещения составит 19 кв. м, остатки денежных средств из выделенных равны нулю, в резерве для покупки – 1 машина типа В. Шестая компонента содержательного смысла не имеет.
Как уже было отмечено, задача линейного программирования с двумя целочисленными переменными может быть решена графически (см. рис. 1). На рисунке 1 полуплоскость, ограниченная прямой (4), соответствует дополнительному ограничению
или
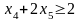 .
.
Однако, для построения этой полуплоскости в дополнительном ограничении необходимо перейти к переменным и следующим образом:
- из системы ограничений модели (2) имеем
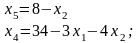
- подставляя эти выражения в дополнительное ограничение вместо переменных и ,получим
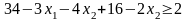
или, после преобразований,
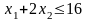 .
.
Прямая (4) на рисунке 1 задана соответствующим полученному неравенству уравнением
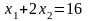 .
.
Достаточно часто при моделировании экономических процессоввстречается особый случай дискретности – двоичность4 переменных. В таких задачах переменные могут принимать только два значения 0 или 1, которые являются своеобразными индикаторами выполнения тех или иных условий.
Пример. Управляющему банком были представлены 4 проекта, претендующие на получение кредита в банке. Ресурс банка в каждый период, потребности проектов и прибыль по ним приведены в таблице (в тыс. долл.).
Проект |
Потребность проекта в объеме кредита |
Прибыль |
||||
Период 1 |
Период 2 |
Период 3 |
Период 4 |
|
||
А |
8 |
8 |
10 |
10 |
21 |
|
Б |
7 |
9 |
9 |
11 |
18 |
|
В |
5 |
7 |
9 |
11 |
16 |
|
Г |
9 |
8 |
7 |
6 |
17,5 |
|
Ресурсы банка |
22 |
25 |
38 |
30 |
|
|
При выборе проектов следует принять во внимание потребности проектов в объемах кредитов и ресурсы банка для соответствующих периодов.
Какие проекты следует финансировать, если цель состоит в том, чтобы максимизировать прибыль?
Решение.
Переменные
задачи
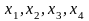 являются двоичными, при этом
являются двоичными, при этом
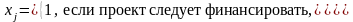
ЭММ задачи имеет обычный вид с дополнительным условием двоичности
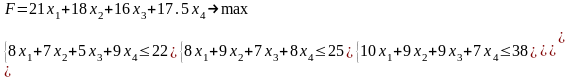
Решение задач с двоичными переменными целесообразно проводить в Excel с использованием надстройки «Поиск решений», позволяющей вводить дополнительно условия как целочисленности, так и двоичности переменных [5]. Результат решения данной задачи в «Поиске решений» приведен на рисунке 2.
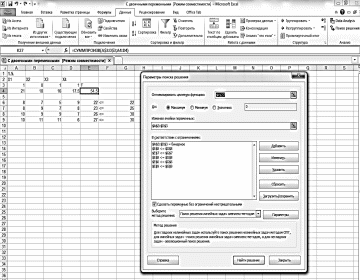
Рисунок 2. Результат решения задачи с двоичными (бинарными) переменными с использованием надстройки «Поиск решений»
2.2.Транспортная задача. Методы построения опорного плана. Улучшение плана методом потенциалов
Транспортную задачу относят к специальным задачам линейного программирования.
Постановка задачи. В т пунктах A1, A2, …, Am(далее – поставщики), сосредоточены некоторые количества однородного продукта (запасы), которые обозначим соответственно аi (i = 1, 2, ..., m). Данный продукт потребляется в п пунктах (далее – потребители) В1, В2, …, Вn; объемы потребления (потребности) равны соответственно bj (j = 1, 2, ..., п). Расходы (тарифы) на перевозку единицы продукта из пункта Ai в пункт Bj равны cij и приведены в матрице транспортных расходовС = (cij). Требуется составить такой план перевозок, при котором суммарные затраты на них были бы минимальны.
Исходные данные транспортной задачи представляют в виде таблицы (см. таблицу 1).
Таблица 1 – Исходные данные транспортной задачи
Поставщики |
Потребители |
Запасы |
||||||
|
|
… |
|
… |
|
|||
|
|
|
… |
|
… |
|
|
|
|
|
|
… |
|
… |
|
|
|
… |
… |
… |
… |
… |
… |
… |
… |
|
|
|
|
… |
|
… |
|
|
|
… |
… |
… |
… |
… |
… |
… |
… |
|
|
|
|
… |
|
… |
|
|
|
Потребности |
|
|
… |
|
… |
|
|
|
Различают открытую и закрытую транспортные задачи.
Если суммарные запасы груза у поставщиков равны суммарным потребностям в грузе потребителей, т.е.
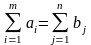 , (*)
, (*)
то задача называется закрытой.
Если равенство (*) не выполняется, то задача открытая.
Экономико-математическая модель закрытой транспортной задачи:
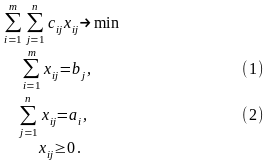
Ограничения означают, что в закрытой транспортной задаче все потребности в грузе потребителей (система (1)) будут удовлетворены и все запасы груза у поставщиков (система (2)) будут вывезены.
Если задача открытая, то возможны два случая:
1) суммарных потребностей больше, чем суммарных запасов, т.е.
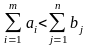 .
.
Тогда не все потребности будут удовлетворены и модель примет вид
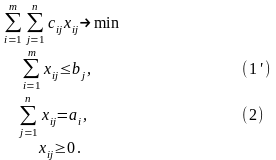
2) суммарных запасов больше, чем суммарных потребностей, т.е.
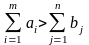 .
.
Тогда не все запасы будут вывезены и модель примет вид

Транспортная задача может быть решена специальными методами, например методом потенциалов, который включает три этапа:
1. Построение первоначального (опорного) плана перевозок, длячего можно использовать различные методы: метод северо-западного угла, наименьших затрат (тарифов), метод аппроксимации Фогеля[2].
Замечание. Сущность этих методов состоит в том, что начальный опорный план находят за не более чем (m+n-1) шагов. При этом число заполненных клеток (число базисных переменных) также оказывается равным (m+n-1) (это одновременно ранг системы линейных уравнений (1) – (2)).Такой план называется невырожденным. Нередко при решении задачи возникает вырожденный план с меньшим числом занятых клеток (когда какие-то из базисных переменных равны 0). В этом случае, как правило, выбирается свободная клетка (или несколько свободных клеток – в зависимости от вырожденности плана) с наименьшим тарифом, которая в дальнейшем формально считается занятой с нулевой перевозкой.
Метод северо-западного угланаиболее прост. Он предполагает заполнение таблицы поставок, начиная с левой верхней клетки (отсюда название «северо-западный угол»). Далее движение осуществляется вниз и вправо до правой нижней клетки. Сразу заметим, что метод северо-западного угла имеет существенный недостаток: полученное им первоначальное распределение достаточно далеко от оптимального решения, так как он построен без учета значений тарифов перевозок.Данный метод допускает модификацию – метод наименьших тарифов, лишенный этого недостатка: на каждом шаге максимально возможную поставку следует давать не в «северо-западную» клетку оставшейся таблицы, а в клетку с наименьшим тарифом перевозки.При этом первоначальное распределение поставок оказывается ближе к оптимальному.
2. Построение системы потенциалов и проверка первоначального плана на оптимальность
Каждой
i-ой
строке (i-му
поставщику) устанавливается потенциал
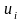 ,
который можно интерпретировать как
цену продукта в соответствующем пункте
поставщика, а каждому j-му
столбцу (j-му
потребителю) устанавливается потенциал
,
который можно интерпретировать как
цену продукта в соответствующем пункте
поставщика, а каждому j-му
столбцу (j-му
потребителю) устанавливается потенциал
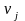 ,
который можно принять условно за цену
продукта в соответствующем пункте
потребителя[7]. В простейшем случае цена
продукта в пункте потребителя равна
его цене в пункте поставщика плюс
транспортные расходы на его доставку,
т.е.
,
который можно принять условно за цену
продукта в соответствующем пункте
потребителя[7]. В простейшем случае цена
продукта в пункте потребителя равна
его цене в пункте поставщика плюс
транспортные расходы на его доставку,
т.е.
= + .
В учебнике [2] представлена связь метода потенциалов и задачи, двойственной к транспортной. При этом потенциалы , – это переменные двойственной задачи.Они показывают, как изменится значение целевой функции транспортной задачи при изменении заданных потребностей (или ресурсов) на одну единицу. Чувствительность оптимального решения транспортной задачи к изменению исходных данных называют постоптимальным анализом.
3. Реализация циклов перераспределения (корректировка плана прикрепления потребителей к поставщикам и объема поставок), после чего переходят к этапу 2.
Этапы 2 и 3 повторяют до тех пор, пока план перевозок не окажется оптимальным по критерию минимальной стоимости затрат на перевозки.
Для решения открытой транспортной задачи методом потенциалов вначале ее приводят к закрытой задаче путем ввода фиктивного потребителя (фиктивного поставщика) потребности (запасы) которого равны разности между суммарными запасами и суммарными потребностями, а тарифы перевозок приравнивают к нулю.
Пример. Найти оптимальное распределение поставок груза для транспортной задачи, исходные данные которой представлены в таблице 2.
Таблица 2 – Исходные данные задачи
Поставщики |
Потребители |
Запасы |
||||
1 |
2 |
3 |
4 |
|
||
1 |
4
|
1 |
2 |
5 |
40 |
|
2 |
3
|
2 |
3 |
7 |
60 |
|
3 |
4
|
4 |
5 |
2 |
90 |
|
Потребности |
45
|
35 |
55 |
65 |
|
|
Решение. Данная задача является открытой, т.к. суммарные запасы груза 40+60+90=190 у поставщиков на 10 единиц меньше, чем суммарные потребности в грузе 45+35+55+65=200 потребителей.
Экономико-математическая модель задачи:
- в компактной форме (с использованием знаков суммирования)
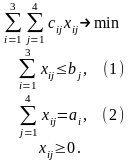
- в развернутом виде
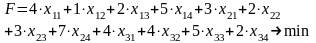
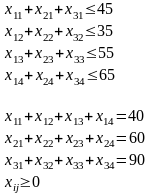
Для решения открытой задачи необходимо ввести фиктивного поставщика, запасы которого будут равны 10 единицам, а тарифы перевозок нулю. Получим новую таблицу 3.
Таблица 3 – Исходные данные с фиктивным поставщиком
Поставщики |
Потребители |
Запасы |
||||
1 |
2 |
3 |
4 |
|
||
1 |
4
|
1 |
2 |
5 |
40 |
|
2 |
3
|
2 |
3 |
7 |
60 |
|
3 |
4
|
4 |
5 |
2 |
90 |
|
Ф |
0
|
0 |
0 |
0 |
10 |
|
Потребности |
45
|
35 |
55 |
65 |
|
|
1 этап.Первоначальное распределение поставок найдем двумя методами:
а)метод северо-западного угла
Заполнение начинаем с левой верхней клетки, то есть с северо-западного угла. Так как потребности первого потребителя равны 45, а возможности первого поставщика – 40, то в клетку с номером (1,1) записываем максимально возможную поставку – 40. Запасы первого поставщика исчерпаны, поэтому первую строку исключаем из рассмотрения (оставшаяся ее часть закрашена штриховкой). Недостающий первому потребителю груз в 5 единиц поставляем за счет запасов второго поставщика. В результате потребность первого потребителя в 45 единиц груза удовлетворена полностью, и первый столбец исключается из рассмотрения. Аналогично продолжаем далее до получения первоначального распределения поставок (см. табл. 4).
Заметим, что занятыми оказались m+n-1=4+4-1=7клеток таблицы.
Первоначальное распределение поставок имеет общую стоимость, равную
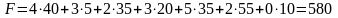 усл.
ден. ед.
усл.
ден. ед.
Замечание.
На каком-либо шаге построения опорного плана транспортной задачи могут оказаться вычеркнутыми и строка, и столбец одновременно. В этом случае первоначальное распределение не будет базисным. Избежать этого можно, используя следующий искусственный прием. Вычеркнув строку (или столбец), перед вычеркиванием столбца (или строки) необходимо осуществить нулевую поставку в его (или ее) свободную клетку с наименьшим тарифом. Далее эта клетка считается занятой.
Таблица 4 – Первоначальное распределение поставок методом северо-западного угла
Поставщики |
Потребители |
Запасы |
||||
1 |
2 |
3 |
4 |
|
||
1 |
4 40 |
1 |
2 |
5 |
40 |
|
2 |
3 5 |
2 35 |
3 20 |
7 |
60 |
|
3 |
4
|
4 |
5 35 |
2 55 |
90 |
|
Ф |
0
|
0 |
0 |
0 10 |
10 |
|
Потребности |
45
|
35 |
55 |
65 |
|
|
б)метод наименьших затрат(тарифов)
Находим в таблице поставок клетки с наименьшими тарифами. Таких клеток четыре – (4,1), (4,2), (4,3), (4,4). Их тарифы равны 0. Сравним максимально возможные поставки для этих клеток:
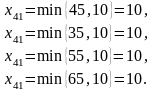
Так как они совпадают, то максимально возможную поставку 10 даем в любую из них, например, в клетку (4,4). В результате запасы фиктивного поставщика вывезены полностью, и четвертая строка таблицы выпадает из последующего рассмотрения.
В
оставшейся таблице наименьший тариф,
равный 1, в клетке с номером (1,2). Максимально
возможная поставка в нее
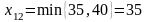 .
Второй столбец выпадает из рассмотрения.
.
Второй столбец выпадает из рассмотрения.
Минимальный тариф теперь в клетках (1,3) и (3,4). Сравним максимально возможные поставки:
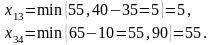
Таким образом, максимальное значение поставки 55 ставим в клетку (3,4). Четвертый столбец выходит из рассмотрения.
Далее аналогично заполняем клетки (1,3), (2,3), (2,1), (3,1). В результате получим первоначальное распределение, представленное в таблице 5.
Таблица 5 – Первоначальное распределение поставок методом наименьших затрат
Поставщики |
Потребители |
Запасы |
||||
1 |
2 |
3 |
4 |
|
||
1 |
4
|
1 35 |
2 5 |
5 |
40 |
|
2 |
3 10 |
2 |
3 50 |
7 |
60 |
|
3 |
4 35 |
4 |
5 |
2 55 |
90 |
|
Ф |
0
|
0 |
0 |
0 10 |
10 |
|
Потребности |
45
|
35 |
55 |
65 |
|
|
Заполнено такжеm+n-1=4+4-1=7 клеток.
Первоначальное распределение поставок имеет общую стоимость, равную
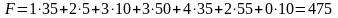 усл.
ден. ед.
усл.
ден. ед.
Видим, что стоимость первоначального распределения поставок меньше в случае использования метода наименьших тарифов. Поэтому далее решаем задачу от первоначального распределения поставок, найденного именно этим методом.
2 Этап.Построение системы потенциалов и проверка начального плана на оптимальность
Потенциалы поставщиков и потребителей определяют для заполненных клеток по формулам
= +
Для начала расчета потенциалов положим u1=0.Тогда
v2= u1+с12=0+1=1, v3= u1+с13=0+2=2, u2= v3-с23=2-3=-1 и т.д.
Результаты расчета потенциалов представлены в последней строке и последнем столбце таблицы 6.
Таблица 6 – Результаты расчета потенциалов
Поставщики |
Потребители |
Запасы |
|
|||||
1 |
2 |
3 |
4 |
|||||
1 |
4
|
1 35 |
2 5 |
5 |
40 |
0 |
||
2 |
3 10 |
2 |
3 50 |
7 |
60 |
-1 |
||
3 |
4 35 |
4 |
5 |
2 55 |
90 |
-2 |
||
Ф |
0
|
0 |
0
|
0 10 |
10 |
0 |
||
Потребности |
45
|
35 |
55 |
65 |
|
|||
|
2 |
1 |
2 |
0 |
||||
Чтобы определить оптимальность распределения, для всех клеток матрицы перевозок определяют их оценки по формулам
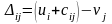 . (3)
. (3)
Используя
ранее принятую интерпретацию, выражение
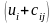 можно трактовать как сумму цены продукта
у поставщика и стоимости перевозки; эта
сумма путем вычитания сравнивается с
ценой продуктау соответствующего
потребителя
можно трактовать как сумму цены продукта
у поставщика и стоимости перевозки; эта
сумма путем вычитания сравнивается с
ценой продуктау соответствующего
потребителя
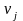 .
Нетрудно
заметить, что оценки занятых клеток
равны нулю (цена потребителя покрывает
цену поставщика и стоимость перевозок).
.
Нетрудно
заметить, что оценки занятых клеток
равны нулю (цена потребителя покрывает
цену поставщика и стоимость перевозок).
Критерий оптимальности формулируется следующим образом:базисное распределение поставок оптимально тогда и только тогда, когда оценки всех свободных клеток неотрицательны.
Если оценка некоторой свободной клетки отрицательна, то это можно интерпретировать так: цена, предлагаемая соответствующим потребителем, больше суммы цены поставщика и стоимости перевозки, то есть если бы эта клетка была занята, то можно было бы получить дополнительный экономический эффект. Следовательно, условием оптимальности распределения служит условие неотрицательности оценок свободных клеток матрицы перевозок.
После расчетов по формуле (3) матрица оценок примет вид
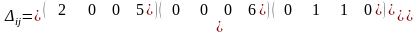 .
.
Пояснение к определению оценок:
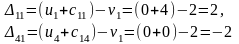
и т.д.
Так как в матрице оценок есть отрицательные значения, то критерий оптимальности не выполняется. Необходимо произвести перераспределение поставок.
3 этап.Реализация циклов перераспределения (корректировка плана прикрепления потребителей к поставщикам и объемов поставок).
В результате перераспределения должна быть заполнена клетка с наименьшей отрицательной оценкой. У нас таких клеток две (4,1) и (4,3). Выберем для заполнения любую из них, например, клетку (4,3).
С этой клетки начинаем построение контура перераспределения, который изображен в таблице 7.
Таблица 7 – Контур перераспределения
Поставщики |
Потребители |
Запасы |
|
|||||
1 |
2 |
3 |
4 |
|||||
1 |
4
|
1 35 |
2 5 |
5 |
40 |
0 |
||
2 |
3 + 10 |
2 |
3 – 50 |
7 |
60 |
-1 |
||
3 |
4 – 35 |
4 |
5 |
2 + 55 |
90 |
-2 |
||
Ф |
0
|
0 |
0 + |
0 – 10 |
10 |
0 |
||
Потребности |
45
|
35 |
55 |
65 |
|
|||
|
2 |
1 |
2 |
0 |
||||
Поясним правила построения контура: начальная вершина контура лежит в выбранной клетке, а все остальные вершины находятся в занятых клетках; при этом отдельные отрезки контура могут быть только горизонтальными и вертикальными; в занятых вершинах отрезки контура образуют один прямой угол. Нельзя рассматривать, как вершины, клетки, где горизонтальные и вертикальные отрезки контура пересекаются. Отрезки контура могу проходить через занятые клетки.
В вершинах контура расставляются поочередно знаки «+» и «–», начиная со знака «+» в выбранной свободной клетке.
Величина перераспределяемой поставки определяется как наименьшая из величин поставок в вершинах контура со знаком «–». На эту величину увеличиваются поставки в вершинах со знаком «+» и уменьшаются – в вершинах со знаком «–». Если величина перераспределяемой поставки одинакова в нескольких клетках со знаком «–», то освобождается только одна клетка, обычно с наибольшей стоимостью перевозки, а все другие клети остаются занятыми с нулевой поставкой.
В нашем примере наименьшая из величин поставок в вершинах контура со знаком «–» или поставка, передаваемая по циклу, равна
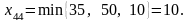 .
.
Передвигая по циклу поставку 10, получим следующее новое распределение поставок (см. табл.8).
Таблица 8 – Новое распределение поставок
Поставщики |
Потребители |
Запасы |
|
|||
1 |
2 |
3 |
4 |
|||
1 |
4
|
1 35 |
2 5 |
5 |
40 |
0 |
2 |
3 20 |
2 |
3 40 |
7 |
60 |
-1 |
3 |
4 25 |
4 |
5 |
2 65 |
90 |
-2 |
Ф |
0
|
0 |
0 10 |
0
|
10 |
2 |
Потребности |
45
|
35 |
55 |
65 |
|
|
|
2 |
1 |
2 |
0 |
|
|
Для нового распределения определяем потенциалы (см. таблицу 8) и составляем матрицу оценок
Так как оценки всех свободных клеток неотрицательны, то получено оптимальное распределение поставок.
Экономические выводы:
1) от первого поставщика целесообразно перевести 35 единиц груза второму потребителю и 5 единиц – третьему, от второго поставщика – 20 единиц – первому потребителю и 40 – третьему и т.д.;
2) все запасы груза от поставщиков будут вывезены, а потребности не полностью будут удовлетворены у третьего потребителя (он получит 45 единиц груза вместо 55, так как еще 10 единиц груза в этом столбце от фиктивного поставщика являются условными);
3) общие суммарные затраты на перевозки будут минимальны и составят
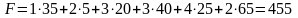 (усл.
ден. ед.).
(усл.
ден. ед.).
Заметим, что полученное оптимальное распределение поставок с найденным минимумом затрат является неединственным, о чем свидетельствует наличие нулевых оценок в незанятых клетках с номерами (2,2) и (4,1).
После определения оптимального решения транспортной задачи интересно задуматься над вопросом: как изменится оптимальное решение при малом изменении потребностей (или ресурсов)? Подобные размышления называют, как уже было отмечено выше,постоптимальным анализом. Соответствующий материал рассмотрен в учебнике [2].
Модификации транспортной задачи
В условии транспортных задач могут встречаться различные ограничения на искомое решение, которые в свою очередь приводят к некоторым модификациям условия, модели и решения транспортной задачи.
К наиболее часто встречающимся ограничениям можно отнести:
1)
запрет
на поставку товара от поставщика
 к
потребителю
(блокировка)
к
потребителю
(блокировка)
Для определения оптимального решения таких задач предполагают, что тариф перевозки единицы грузаот к является сколь угодно большим числом М.
2)
обеспечение
перевозки от поставщика
к потребителю
в точности
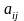 единиц
груза
единиц
груза
В клетку с номером (i,j) записывают указанное число и в дальнейшем эту клетку считают свободной со сколь угодно большим тарифом М.
3) от поставщика к потребителю должно быть завезено не менее единиц груза
Запасы пункта и потребности пункта полагают меньше фактических на единиц. После нахождения оптимального плана перевозку, стоящую в клетке (i,j) увеличивают на единиц.
4) от поставщика к потребителю должно быть завезено не более единиц груза
Вводят
дополнительного потребителя
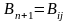 ,
которому записывают те же тарифы, что
и для
,
за исключением тарифа в i-ой
строке, который считают равным сколь
угодно большому числу М.
Потребности пункта
считают равными
,
а потребности
,
которому записывают те же тарифы, что
и для
,
за исключением тарифа в i-ой
строке, который считают равным сколь
угодно большому числу М.
Потребности пункта
считают равными
,
а потребности
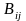 полагают равными
полагают равными
 .
.
Примеры решения задач с ограничениями 1 – 4«вручную» приведены в [2].
При решении модифицированной транспортной задачи с использованием надстройки Excel «Поиск решений» первое ограничение также реализуется изменением в условии задачи: если критерием оптимальности являются минимальные затраты на все перевозки, то для обеспечения запрета тариф перевозки в соответствующей ячейке необходимо сделать сколь угодно большим числом (поставка становится дорогой, а, значит, невыгодной).Второе – четвертоеусловия приводят к введению вмодель задачи, а, значит, и в «Поиск решений», дополнительного ограничения для соответствующей ячейки[1], [5].
При составлении плана перевозок часто весьма важной задачей является экономия времени, даже в ущерб стоимости перевозки. Например, при транспортировке скоропортящихся продуктов необходима их доставка в пункты назначения за минимальное время. В период уборки урожая важно как можно быстрее доставить зерно на заготовительные пункты. К подобным задачам относятся переброска сил быстрого реагирования в районы стихийного бедствия, доставка медицинских грузов и другие аналогичные задачи. Модели подобных задач уже не являются задачами линейного программирования, так как их целевые функции не линейны. Рассмотрение таких задач выходит за рамки данного пособия. Алгоритм решения транспортной задачи по критерию времени приведен в учебнике [2].
Задача о назначениях
Частным случаем транспортной задачи, а такжехарактерным примером задачи с двоичными (булевыми) переменными является задача о назначениях. Задача о назначениях – это распределительная задача, в которой для выполнения каждой работы требуется один и только один ресурс (один человек, одна автомашина и т.д.), и каждый ресурс может быть использован на одной и только одной работе. Задача о назначениях имеет место при распределении людей на должности или работы, автомашин на маршруты, водителей на машины, групп по аудиториям, научных тем по научно-исследовательским лабораториям и т.п.
Исторически задача об оптимальном назначении была первой задачей линейного программирования. Ее решение впервые было предложено в 1931 г. венгерским математиком Эгервари.
Постановка
задачи.
Имеется n
видов работ и n
исполнителей этих работ. Известны
экономические оценки эффекта
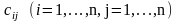 от назначения i-го
исполнителя на j-й
вид работ. Требуется так распределить
исполнителей по видам работ, чтобы
суммарный эффект от назначений был
максимальным.
от назначения i-го
исполнителя на j-й
вид работ. Требуется так распределить
исполнителей по видам работ, чтобы
суммарный эффект от назначений был
максимальным.
Экономико-математическая модель задачи.Так как количество работ равно числу исполнителей, то задача закрытая. В этом случае все исполнители будут назначены, и все работы будут выполняться. Введем необходимые обозначения.Пусть, если
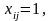 то
работник i
назначен на операцию j;
то
работник i
назначен на операцию j;
если
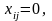
то работник i не назначен на операцию j.
Тогда математически задачу о назначениях можно записать в виде
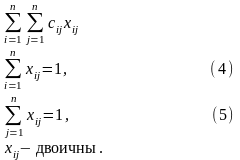
Получили транспортную задачу с единичными ресурсами и потребностями.Система (4) означает, что каждый исполнитель будет назначен на выполнение единственной работы, а система (5) – каждая работа будет выполняться единственным исполнителем. Решение задачи о назначениях можно получить методом потенциалов[2]или с использованием надстройки«Поиск решения» в Excel[3], [5].
Если количество работ и их исполнителей не совпадают, то задача будет открытой. Тогда одна из систем (4) или (5) будет системой неравенств знака « ».
В задачах о назначениях, как и в транспортных задачах, могут встречаться модификации в виде запрета на назначение в соответствующую ячейку, которые реализуются изменениями в условии задачи (например, полагаютвремя выполнения соответствующих работ сколь угодно большим, объем продаж сколь угодно малым и т.п.).
Задачи для самостоятельного решения
Задание 1. Решить задачу целочисленного программирования:
а) графическим способом;
б) методом Гомори;
в) дать геометрическую интерпретацию введения дополнительного ограничения.
Варианты 1.1 – 1.10
|
|||
1.1 |
|
1.2 |
|
1.3 |
|
1.4 |
|
1.5 |
|
1.6 |
|
1.7 |
|
1.8 |
|
1.9 |
|
1.10 |
|
Задание 2. Исходные данные транспортных задач приведены в транспортных таблицах. Сформулировать экономико-математическую модель задачи, найти оптимальный план закрепления поставщиков за потребителями, установить единственность или не единственность оптимального плана. Проверить полученное решение средствами Excel.
Варианты 2.1 – 2.10
2.1. Транспортная таблица
Поставщики
|
Потребители |
Запасы |
|||
В1 |
В2 |
В3 |
В4 |
||
А1 |
9 |
5 |
10 |
7 |
70 |
А2 |
11 |
8 |
9 |
6 |
80 |
А3 |
7 |
6 |
5 |
4 |
90 |
А4 |
6 |
4 |
3 |
2 |
100 |
Потребности |
150 |
40 |
110 |
50 |
|
2.2. Транспортная таблица
Поставщики
|
Потребители |
Запасы |
||||
В1 |
В2 |
В3 |
В4 |
В5 |
||
А1 |
5 |
3 |
4 |
6 |
4 |
40 |
А2 |
3 |
4 |
10 |
5 |
7 |
20 |
А3 |
4 |
6 |
9 |
3 |
4 |
40 |
Потребности |
25 |
10 |
20 |
30 |
15 |
|
2.3. Транспортная таблица
Поставщики
|
Потребители |
Запасы |
|||
В1 |
В2 |
В3 |
В4 |
||
А1 |
5 |
4 |
3 |
2 |
100 |
А2 |
2 |
3 |
5 |
6 |
60 |
А3 |
3 |
2 |
4 |
3 |
80 |
А4 |
4 |
1 |
2 |
4 |
160 |
Потребности |
100 |
140 |
100 |
60 |
|
2.4. Транспортная таблица
Поставщики
|
Потребители |
Запасы |
||||
В1 |
В2 |
В3 |
В4 |
В5 |
||
А1 |
3 |
3 |
5 |
3 |
1 |
500 |
А2 |
4 |
3 |
2 |
4 |
5 |
300 |
А3 |
3 |
7 |
5 |
4 |
1 |
100 |
Потребности |
150 |
350 |
200 |
100 |
100 |
|
2.5. Транспортная таблица
Поставщики
|
Потребители |
Запасы |
|||
В1 |
В2 |
В3 |
В4 |
||
А1 |
4 |
8 |
1 |
6 |
70 |
А2 |
3 |
5 |
3 |
4 |
80 |
А3 |
2 |
6 |
4 |
3 |
90 |
А4 |
1 |
4 |
5 |
3 |
80 |
Потребности |
60 |
40 |
120 |
100 |
|
2.6. Транспортная таблица
Поставщики
|
Потребители |
Запасы |
||||
В1 |
В2 |
В3 |
В4 |
В5 |
||
А1 |
4 |
2 |
3 |
4 |
1 |
60 |
А2 |
2 |
4 |
3 |
5 |
6 |
90 |
А3 |
6 |
5 |
4 |
6 |
2 |
140 |
Потребности |
40 |
30 |
90 |
80 |
50 |
|
2.7. Транспортная таблица
Поставщики
|
Потребители |
Запасы |
||||
В1 |
В2 |
В3 |
В4 |
В5 |
||
А1 |
5 |
15 |
3 |
6 |
10 |
9 |
А2 |
23 |
8 |
13 |
27 |
12 |
11 |
А3 |
30 |
1 |
5 |
24 |
25 |
14 |
Потребности |
8 |
9 |
13 |
8 |
12 |
|
2.8. Транспортная таблица
Поставщики
|
Потребители |
Запасы |
|||
В1 |
В2 |
В3 |
В4 |
||
А1 |
2 |
4 |
5 |
1 |
60 |
А2 |
2 |
3 |
9 |
4 |
70 |
А3 |
8 |
4 |
2 |
5 |
50 |
Потребности |
40 |
30 |
20 |
50 |
|
2.9. Транспортная таблица
Поставщики
|
Потребители |
Запасы |
||||
В1 |
В2 |
В3 |
В4 |
В5 |
||
А1 |
3 |
4 |
5 |
15 |
24 |
15 |
А2 |
19 |
2 |
22 |
4 |
13 |
15 |
А3 |
20 |
27 |
1 |
17 |
19 |
15 |
Потребности |
11 |
11 |
11 |
16 |
11 |
|
2.10. Транспортная таблица
Поставщики
|
Потребители |
Запасы |
||||
В1 |
В2 |
В3 |
В4 |
В5 |
||
А1 |
16 |
30 |
17 |
10 |
16 |
4 |
А2 |
20 |
27 |
26 |
9 |
23 |
6 |
А3 |
13 |
4 |
22 |
3 |
1 |
10 |
А4 |
3 |
1 |
5 |
4 |
24 |
10 |
Потребности |
7 |
7 |
7 |
7 |
2 |
|
Задание 3.Сформулировать экономико-математическую модель транспортной задачи, найти оптимальный план перевозок груза от поставщиков к потребителям. Сделать выводы экономического характера. Решение «вручную» проверить средствами Excel.
Варианты 3.1 – 3.10
Задачи 3.1 – 3.5. Минимизировать расходы на доставку продукции со складов фирмы магазинам-заказчикам. Тарифы на перевозку единицы продукции, объёмы запасов продукции на складах и объёмы заказанной продукции представлены в матрицах перевозок.
3.1. Матрица перевозок
Магазин
Склад |
Магазины-заказчики |
Запасы на складе (ед. прод.) |
||||
«Анна» |
«Вада» |
«Ева» |
«Алла» |
«Мех» |
||
«Таганка» |
1 |
3 |
4 |
5 |
2 |
20 |
«ВВЦ» |
2 |
1 |
1 |
4 |
5 |
15 |
«Щёлково» |
1 |
3 |
3 |
2 |
1 |
40 |
«Коньково» |
3 |
1 |
4 |
2 |
3 |
15 |
Объём заказа (ед. прод.) |
15 |
10 |
25 |
5 |
9 |
|
3.2. Матрица перевозок
Магазин
Склад |
«Росстек» |
«Шер» |
«Ткани»
|
«Мода» |
«Вита» |
Запасы на складе (ед.прод.) |
Иваново |
12 |
14 |
32 |
20 |
3 |
54 |
Москва |
8 |
10 |
12 |
24 |
12 |
32 |
Новгород |
6 |
8 |
12 |
24 |
8 |
85 |
Серпухов |
10 |
18 |
4 |
8 |
9 |
162 |
Объём заказа (ед.прод.) |
100 |
70 |
30 |
45 |
50 |
|
3.3. Матрица перевозок
Магазин
Склад |
«Всё для дома» |
«Здоровый сон» |
«Фея» |
«Ночное царство» |
«Мех» |
Запасы на складе (ед.прод.) |
«Вороново» |
1 |
3 |
4 |
5 |
2 |
20 |
«Фили» |
2 |
1 |
1 |
4 |
5 |
15 |
«Беляево» |
1 |
3 |
3 |
2 |
1 |
40 |
«Выхино» |
3 |
1 |
4 |
2 |
3 |
15 |
Объём заказа (ед.прод.) |
15 |
10 |
25 |
5 |
9 |
|
3.4. Матрица перевозок
Магазин
Склад |
ВДНХ
|
Юго- Западная |
Фили |
Арбатская |
Сокольники |
Запасы на складе (ед.прод.) |
Пролетарская |
10 |
8 |
3 |
15 |
16 |
60 |
Митино |
7 |
5 |
9 |
4 |
6 |
30 |
Строгино |
2 |
0 |
14 |
5 |
20 |
40 |
Объём заказа (ед.прод.) |
10 |
20 |
40 |
30 |
65 |
|
3.5. Матрица перевозок
Магазин
Склад |
Тверь
|
Рязань |
Тула |
Чехов |
Запасы на складе (ед.прод.) |
Москва |
5 |
3 |
7 |
2 |
25 |
Санкт-Петербург |
2 |
6 |
4 |
5 |
36 |
Саратов |
3 |
7 |
1 |
9 |
40 |
Самара |
6 |
4 |
8 |
3 |
50 |
Объём заказа (ед.прод.) |
20 |
45 |
15 |
25 |
|
Задачи 3.6 – 3.10. Компания, занимающаяся ремонтом автомобильных дорог, в следующем месяце будет проводить ремонтные работы на пяти участках автодорог. Песок на участки ремонтных работ может доставляться из трех карьеров, месячные объемы предложений по карьерам известны. Из планов производства ремонтных работ известны месячные объемы потребностей по участкам работ. Имеются экономические оценки транспортных затрат (в у.е.) на перевозку 1тонны песка с карьеров на ремонтные участки.Числовые данные для решения содержатся ниже в матрицах планирования (повариантам).
Требуется:
1) Предложить план перевозок песка на участки ремонта автодорог, который обеспечивает минимальные совокупные транспортные издержки.
2) Что произойдет с оптимальным планом, если изменятся условия перевозок:
а) появится запрет на перевозки от первого карьера до второго участка работ?
б) от второго карьера до третьего участка работ объем перевозок будет не менее (не более, ровно)3 т?
3.6. Матрица планирования:
Участки работ
Карьеры |
В1
|
В2
|
В3 |
В4 |
В5 |
Предложение
|
А1 |
5
|
3
|
4 |
6
|
4
|
40
|
А2
|
3
|
4
|
10 |
5
|
7
|
20
|
А3
|
4
|
6
|
9 |
3
|
4
|
40
|
Потребности |
25 |
10 |
20 |
30 |
15 |
|
3.7. Матрица планирования:
Участки работ
Карьеры |
В1
|
В2
|
В3 |
В4
|
В5 |
Предложение
|
А1 |
3
|
3
|
5 |
3
|
1
|
500
|
А2
|
4
|
3
|
2 |
4
|
5
|
300
|
А3 |
3
|
7
|
5 |
4
|
1
|
100
|
Потребности |
150 |
350 |
200 |
100 |
100 |
|
3.8. Матрица планирования:
Участки работ
Карьеры |
В1
|
В2
|
В3 |
В4
|
В5 |
Предложение
|
А1 |
4
|
2
|
3 |
4
|
1
|
60
|
А2
|
2
|
4
|
3 |
5
|
6
|
90
|
А3
|
6
|
5
|
4 |
6
|
2
|
140
|
Потребности |
40 |
30 |
90 |
80 |
50 |
|
3.9. Матрица планирования:
Участки работ
Карьеры |
В1
|
В2
|
В3 |
В4
|
В5 |
Предложение
|
А1 |
5
|
15
|
3 |
6
|
10
|
9
|
А2
|
23
|
8
|
13 |
27
|
12
|
11
|
А3
|
30
|
1
|
5 |
24
|
25
|
14
|
Потребности |
8 |
9 |
13 |
8 |
12 |
|
3.10. Матрица планирования:
Участки работ
Карьеры |
В1
|
В2
|
В3 |
В4
|
В5 |
Предложение
|
А1 |
3
|
4
|
5 |
15
|
24
|
15
|
А2
|
19
|
2
|
22 |
4
|
13
|
15
|
А3
|
20
|
27
|
1 |
17
|
19
|
15
|
Потребности |
11 |
11 |
11 |
16 |
11 |
|
Задание 4. Сформулировать экономико-математическую модель дискретнойзадачи линейного программирования, найти ее оптимальный план. Сделать выводы экономического характера. При решении задачи воспользоваться средствами Excel.
Варианты 4.1 – 4.10
4.1.Компания «Корвет» производит программное обеспечение на CD-ROM.Компания оценивает возможность развития шести новых программных приложений. В таблице представлена информация о затратах и ожидаемой чистой прибыли от продажи приложений (в тыс. долл.).
Приложение |
Затраты на развитие |
Число программистов |
Чистая прибыль |
П1 |
400 |
6 |
2000 |
П2 |
1100 |
18 |
3600 |
П3 |
940 |
20 |
4000 |
П4 |
760 |
16 |
3000 |
П5 |
1260 |
28 |
4400 |
П6 |
1800 |
34 |
6200 |
Ресурсы |
3500 |
60 |
|
У «Корвета» 60 программистов. На развитие новых программных приложений фирма может выделить 3,5 млн долл.
Каков оптимальный набор приложений, которые следует развивать, если:
1) ожидается, что клиенты, заинтересованные в приложении П4, будут заинтересованы также в приложении П5 и наоборот. Таким образом, эти приложения должны либо вместе развиваться, либо вместе не развиваться;
2) развитие приложения П1 имеет смысл только при наличии приложения П2. Таким образом, если развивается приложение П1, должно развиваться и приложение П2, но приложение П2 может развиваться и без приложения П1;
3) развиваться может только одно из приложений П3 и П6;
4) стремясь обеспечить качество продукции, «Корвет» не склонен развивать более трех программных продуктов.
Проанализируйте влияние каждого из четырех перечисленных ограничений на оптимальное решение.
4.2.Некоторая компания рассматривает возможность реализации шести проектов в течениечетырех лет.Компания может выполнить любой проект частично или полностью. При частичном выполнении проекта доход и затраты рассчитываются пропорционально реализованной доле проекта.
Ожидаемые затраты на реализацию каждого проекта и доход от них приведены в таблице.
Проект |
Затраты на весь проект |
Доход от всего проекта |
||||
1 год |
2 год |
3 год |
4 год |
|
||
1 |
10,5 |
14,4 |
2,2 |
2,4 |
32,4 |
|
2 |
8,3 |
12,6 |
9,5 |
3,1 |
35,8 |
|
3 |
10,2 |
14,2 |
5,6 |
4,2 |
17,75 |
|
4 |
7,2 |
10,5 |
7,5 |
5 |
14,8 |
|
5 |
12,3 |
10,1 |
8,3 |
6,3 |
18,2 |
|
6 |
9,2 |
7,8 |
6,9 |
5,1 |
12,35 |
|
Возможное вложение (в тыс. долл.) |
60 |
70 |
35 |
20 |
|
|
Сформулируйте ЗЛП и найдите решение (состоящее из набора выполняемых частей проектов), максимизирующее общую прибыль.
4.3. Хлебозавод имеет возможность производить различные хлебобулочные изделия. Нормы затрат различных типов сырья, их наличие и стоимость единицы продукции каждого вида приведены в таблице.
Сырье |
Нормы затрат |
Наличие, кг |
|||
Хлеб «Бородинский» |
Хлеб «Жито» |
Батон «Чайный» |
Батон «Городской» |
||
Мука пшеничная |
0,2 |
0,15 |
0,4 |
0,35 |
500 |
Мука ржаная |
0,25 |
0,3 |
- |
- |
250 |
Яйцо |
0,02 |
0,025 |
0,04 |
0,035 |
100 |
Масло |
0,01 |
0,03 |
0,1 |
0,15 |
200 |
Дрожжи |
0,005 |
0,005 |
0,01 |
0,01 |
15 |
Вес изделия |
0,65 |
0,85 |
0,7 |
0,6 |
|
Стоимость одного изделия |
7 |
8 |
9 |
8 |
|
После проведения маркетинговых исследований установлено, что ежедневный спрос на «Бородинский» хлеб колеблется в пределах от 150 до 300 кг; спрос на хлеб «Жито» меняется соответственно от 300 до 450 кг; на батон «Чайный» – от 200 до 300 кг; на батон «Городской» – от 200 до 400 кг. Определить оптимальный ежедневный объем выпускаемой хлебобулочной продукции, обеспечивающий максимальную ее стоимость.
4.4. Фирма собирается разрабатывать пять новых программных продуктов. Потребности проектов, денежные ресурсы фирмы в каждомиз кварталов и ожидаемая прибыль от реализации программныхпродуктов представлены в таблице. Разработку каких программныхпродуктов следует финансировать, чтобы получить наибольшуюприбыль?
Период |
Программные продукты |
Ресурс фирмы |
|||||
А |
Б |
В |
Г |
Д |
|||
1 кв. |
4 |
7 |
11 |
2 |
12 |
34 |
|
2 кв. |
5 |
9 |
8 |
6 |
7 |
30 |
|
3 кв. |
2 |
9 |
- |
9 |
3 |
27 |
|
4 кв. |
2 |
4 |
- |
9 |
- |
39 |
|
Прибыль |
12 |
21 |
10 |
18 |
19 |
|
|
4.5. Управляющему банком предложены четыре проекта, претендующие на получение кредита в банке. Ресурс банка в каждом периоде, потребности проектов и прибыль по ним приведены в таблице (в усл. ед.):
Проект |
Потребности проектов в объемах кредитов |
Прибыль |
||||
Период 1 |
Период 2 |
Период 3 |
Период 4 |
|
||
А |
8 |
8 |
10 |
10 |
34 |
|
Б |
7 |
9 |
9 |
11 |
30 |
|
В |
5 |
7 |
9 |
11 |
27 |
|
Г |
9 |
8 |
7 |
6 |
39 |
|
Ресурс банка |
22 |
25 |
38 |
30 |
|
|
Какие проекты следует финансировать, если цель состоит в максимизации прибыли банка от кредитования?
4.6. В распоряжении некоторой компании имеется 6 торговых точек и 6 продавцов. Из прошлого опыта известно, что эффективность работы продавцов в различных торговых точках неодинакова. Коммерческий директор компании произвел оценку деятельности каждого продавца в каждой торговой точке. Результаты этой оценки представлены в таблице:
-
Продавец
Объемы продаж по торговым точкам, USD/тыс.шт.
I
II
III
IV
V
VI
A
68
72
75
-
75
69
B
56
60
58
63
61
59
C
35
38
40
45
25
27
D
40
42
47
45
53
36
E
62
70
68
67
69
70
F
65
63
69
70
72
68
Назначение первого продавца на четвертую торговую точкунедопустимо по медицинским показаниям, поэтому в матрице объемов продаж проставлен запрет – «-».
Как коммерческий директор должен осуществить назначение продавцов по торговым точкам, чтобы достичь максимального объема продаж?
4.7. В распоряжении некоторой компании имеется 6 торговых точек и 5 продавцов. Из прошлого опыта известно, что эффективность работы продавцов в различных торговых точках неодинакова. Коммерческий директор компании произвел оценку деятельности каждого продавца в каждой торговой точке. Результаты этой оценки представлены в таблице:
Продавец |
Объемы продаж по торговым точкам, USD/тыс.шт. |
|||||
I |
II |
III |
IV |
V |
VI |
|
A |
68 |
72 |
75 |
83 |
75 |
69 |
B |
56 |
60 |
58 |
63 |
61 |
59 |
C |
35 |
38 |
40 |
45 |
25 |
27 |
D |
40 |
42 |
47 |
45 |
53 |
36 |
E |
62 |
70 |
68 |
67 |
69 |
70 |
Как коммерческий директор должен осуществить назначение продавцов по торговым точкам, чтобы достичь максимального объема продаж?
4.8. Мастер должен назначить на 10 типовых операций 12 рабочих. Данные о времени, которое затрачивают рабочие на выполнение каждой операции, приведены в матрице эффективностей назначений:
Операции Рабочие |
О1 |
О2 |
О3 |
О4 |
О5 |
О6 |
О7 |
О8 |
О9 |
О10 |
Р1 |
29 |
31 |
16 |
16 |
17 |
34 |
20 |
28 |
16 |
13 |
Р2 |
29 |
25 |
22 |
30 |
24 |
31 |
37 |
23 |
16 |
27 |
Р3 |
27 |
32 |
- |
14 |
34 |
30 |
27 |
16 |
19 |
17 |
Р4 |
21 |
35 |
- |
32 |
31 |
28 |
30 |
29 |
31 |
16 |
Р5 |
21 |
36 |
- |
14 |
24 |
30 |
21 |
28 |
29 |
27 |
Р6 |
28 |
35 |
25 |
30 |
22 |
16 |
- |
18 |
25 |
18 |
Р7 |
27 |
34 |
33 |
26 |
14 |
19 |
18 |
37 |
19 |
16 |
Р8 |
27 |
34 |
27 |
30 |
37 |
37 |
26 |
22 |
35 |
33 |
Р9 |
16 |
26 |
18 |
26 |
16 |
20 |
31 |
34 |
28 |
29 |
Р10 |
16 |
22 |
33 |
22 |
21 |
19 |
19 |
37 |
36 |
24 |
Р11 |
26 |
35 |
13 |
14 |
17 |
36 |
17 |
17 |
25 |
21 |
Р12 |
34 |
25 |
19 |
14 |
36 |
36 |
17 |
36 |
26 |
33 |
В матрице эффективностей назначений проставлен запрет «-», если рабочий не может выполнять соответствующую операцию.
Сформировать план распределения рабочих по операциям, при котором суммарное время на выполнение работ будет минимально.
4.9. Администрация деревоперерабатывающего предприятия «Смена» приняла на работу пять человек. Каждый из них имеет различные способности и навыки и затрачивает различное время на выполнение определенной работы. В настоящее время необходимо выполнить пять видов работ. Время выполнения работы каждым работником приведено в таблице:
Время выполнения, час. Работник |
Работа 1
|
Работа 2 |
Работа 3 |
Работа 4 |
Работа 5 |
Р1 |
25 |
16 |
15 |
14 |
13 |
Р2 |
25 |
17 |
18 |
23 |
15 |
Р3 |
30 |
15 |
20 |
19 |
14 |
Р4 |
27 |
20 |
22 |
25 |
12 |
Р5 |
29 |
19 |
17 |
32 |
10 |
1) Требуется назначить на каждый вид работы одного из работников. Как это следует сделать, чтобы общее время, необходимое для завершения всех видов работ, было минимальным?
2) Предприятие «Смена» может принять на работу еще одного рабочего по совместительству, который выполняет каждую работу в течение следующего времени:
Время выполнения, час. Работник- совместитель |
Работа 1 |
Работа 2 |
Работа 3 |
Работа 4 |
Работа 5 |
Р6 |
28 |
16 |
19 |
16 |
15 |
Требуется определить, каким образом данная мера повлияет на назначение рабочих и минимизацию общего времени выполнения работ.
4.10. Фирма получила заказы на выполнение ремонтных работ на пяти объектах (евроремонт пяти квартир). Для выполнения этих заказов фирма располагает шестью бригадами, каждая из этих бригад выполняет один заказ «под ключ». Ниже в таблице приведены оценки времени (в днях), необходимого бригадам для выполнения всех работ и сдачи объектов заказчикам (исходя из состава и квалификации работников бригады).Оценки даны бригадирами и опыт работы их в фирме дает основания руководству доверять им.
Время выполнения, чел.-дни Бригада |
Объект 1
|
Объект 2 |
Объект 3 |
Объект 4 |
Объект 5 |
Р1 |
47 |
60 |
25 |
63 |
68 |
Р2 |
48 |
57 |
33 |
56 |
71 |
Р3 |
45 |
53 |
20 |
62 |
61 |
Р4 |
48 |
60 |
18 |
65 |
74 |
Р5 |
44 |
66 |
21 |
61 |
76 |
Р6 |
42 |
54 |
29 |
55 |
69 |
Распределить объекты работ между бригадами, чтобы общее количество человеко-дней, затраченное на выполнение работ на всех пяти объектах, было минимальным.
Раздел 3. Задачи многокритериальной оптимизации
3.1. Происхождение и постановка задачи многокритериальной оптимизации
При практическом выборе экономических решений важным является случай, когда степень достижения цели, которую желательно оптимизировать (объем продукции, объем издержек и пр.), невозможно представить одной величиной. Существует многообразие целей.
Примеры
1. Задачи такого рода встречаются, когда в результате производственного процесса получается ряд различных продуктов, количества которых невозможно суммировать, или когда на производство влияет несколько факторов, количество которых невозможно выразить в одной единице измерения.
2. Принятие решения о строительстве дороги в объезд города должно учитывать такие факторы, как выигрыш города в целом по соображениям экологии, проигрыш отдельных предприятий и фирм, например, из-за уменьшения проезжающих через город потенциальных покупателей и многие другие.
Если такие задачи решаются методами математического программирования, то говорят о задачахмногокритериальной оптимизации. Эти задачи могут носить как линейный, так и нелинейный характер. Ниже мы рассмотрим методы решения таких задач для линейного случая.
Задачи многокритериальной оптимизации сводятся к поиску лучшего (оптимального) решения при наличии различных несводимых друг к другу критериев оптимальности. Требуется найти точку области допустимых решений (ОДР), которая минимизирует или максимизирует все такие критерии.Заметим, что различают количественные и качественные критерии. Последние не всегда правильно используются на практике.
Примеры на составление модели многокритериальной задачи
1.Рекламное агентство, в штате которого 10 человек, получило заказ на рекламу нового продукта на радио и телевидении (ТВ). Данные о рекламной аудитории, стоимости рекламы и количестве занятых при ее изготовлении агентов даны в таблице.
Характеристики |
Радио |
Телевидение |
Рекламная аудитория (млн чел.) |
4 |
8 |
Стоимость минуты рекламы (в тыс. у.е.) |
8 |
24 |
Количество занятых агентов |
1 |
2 |
Сколько минут рекламного времени должно купить агентство на радио и ТВ, чтобы максимизировать аудиторию и минимизировать свои издержки, если контракт запрещает использовать более 6 минут рекламы на радио?
Экономико-математическая модель.Если – количество заказанных минут на радио, а – на ТВ, то имеем следующую задачу:

2.Если в многокритериальных задачах речь идет не о разнородных критериях некоторой системы, а о сопоставлении однородных критериев разных ее подсистем (например, отрасли, группы населения и т.п.), то эти задачи называются задачами векторной оптимизации.
Рассмотрим общий видмоделитакой задачи.
Обозначим
i-й
частный критерий через
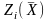 ,
где
,
где
 –
допустимое решение, а область допустимых
решений или множество
достижимых критериальных векторов
– через Q.
Если
учесть, что изменением знака функции
всегда можно свести задачу минимизации
к задаче максимизации, то кратко задачу
многокритериальной оптимизации можно
сформулировать следующим образом:
–
допустимое решение, а область допустимых
решений или множество
достижимых критериальных векторов
– через Q.
Если
учесть, что изменением знака функции
всегда можно свести задачу минимизации
к задаче максимизации, то кратко задачу
многокритериальной оптимизации можно
сформулировать следующим образом:
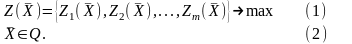
Полученную модель можно считать задачей многокритериальной оптимизации в общей постановке.
3.2. Основные методы решения многокритериальных задач
Некоторые частные критерии могут противоречить друг другу, другие действуют в одном направлении, третьи – индифферентны, т.е. безразличны друг к другу. Поэтому процесс решения многокритериальных задач неизбежно связан с экспертными оценками, как самих критериев, так и взаимоотношений между ними.
Выделяют ряд методов решения задач многокритериальной оптимизации:
1) оптимизация одного, признанного наиболее важным критерия, остальные критерии при этом играют роль дополнительных ограничений;
2) сведение многих критериев к одному введением экспертных весовых коэффициентов для каждого из критериев таким образом, что более важный критерий получает более высокий вес;
3) упорядочение заданного множества критериев и последовательная оптимизация по каждому из них (этот подход лежит в основе метода последовательных уступок).
Доминирование и оптимальность по Парето. Эффективные решения и паретова граница
В идеальном случае многокритериальной задачи можно вести поиск такого решения, которое принадлежит пересечению множеств оптимальных решений всех однокритериальных задач. Однако такое пересечение обычно оказывается пустым множеством, поэтому приходится рассматривать так называемое переговорное множество эффективных решений (оптимальных по Парето). Критерий оптимальности итальянского экономиста В. Парето применяется при решении таких задач, когда оптимизация означает улучшение одних показателей при условии, что другие не ухудшаются.
Определение.
Вектор
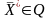 называется эффективным (оптимальным
по Парето) решением задачи (1), (2), если
не существует такого вектора
называется эффективным (оптимальным
по Парето) решением задачи (1), (2), если
не существует такого вектора
 ,
что
,
что

причем хотя бы для одного значения i имеет место строгое неравенство.
Пример. Метод «стоимость – эффективность»
Пусть
заданы два критерия:
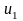 – стоимость,
– стоимость,
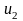 – эффективность. Рассмотрим задачу
– эффективность. Рассмотрим задачу
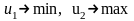 .
.
Множество допустимых вариантов U в пространстве критериев графически представлено на рисунке 1.
Рисунок 1. Множество допустимых вариантов U в пространстве критериев
Рассмотрим два допустимых варианта 1 и 2. Вариант 1 имеет большую эффективность и меньшую стоимость, чем 2, следовательно, вариант 1 лучше. Если сравнивать варианты 1 и 3, то видно, что вариант 1 имеет меньшую стоимость, но вариант 3 более эффективен. В этом случае можно сказать, что варианты 1 и 3 несравнимы.
Множество всех допустимых вариантов, для которых не существует вариантов лучше, находится на дуге АВ. Все эти варианты несравнимы между собой и называются Парето-оптимальными вариантами.
Множество допустимых решений, для которых невозможно одновременно улучшить все частные показатели эффективности (т.е. улучшить хотя бы один из них, не ухудшая остальных), принято называть областью Парето, или областью компромиссов, а принадлежащие ей решения – эффективными, или оптимальными по Парето.
В общем случае эффективные решения не эквивалентны друг другу, так что про два оптимальных по Парето решения нельзя сказать, какое из них лучше. Поэтому при решении многокритериальных задач необходимо дополнительное изучение эффективных решений. Для этого можно было бы сформулировать некоторый критерий и оптимизировать его на множестве эффективных решений. Однако при этом возникают значительные трудности в связи с тем, что, как правило, область компромиссов не является выпуклой, и полученная задача в общем случае будет задачей невыпуклого программирования.
Свертка критериев с весовыми коэффициентами. Метод обобщенного критерия
Обычный подход заключается в стремлении «свернуть» частные критерии в один обобщенный скалярный критерий, оптимизация которого приводит к оптимальному решению задачи в целом. Формулировка подходящего обобщенного критерия в зависимости от конкретных условий как раз и является основным вопросом, который изучается в многокритериальной оптимизации.
Методы параметрического программирования.
Метод последовательных уступок
В некоторых случаях вместо одного обобщенного критерия и решения одной соответствующей задачи скалярной оптимизации предлагается рассматривать последовательность обобщенных критериев и последовательность задач скалярной оптимизации. Рассмотрим один из таких методов решения многокритериальных задач – метод последовательных уступок.Этот метод применяется в случае, когда частные критерии могут быть упорядочены в порядке убывания их важности.
Предположим,
что все частные критерии максимизируются
и пронумерованы в порядке убывания их
важности. Находим максимальное значение
 первого по важности критерия в области
допустимых решений путем решения
однокритериальной задачи
первого по важности критерия в области
допустимых решений путем решения
однокритериальной задачи

Затем,
исходя из практических соображений и
принятой точности, назначается величина
допустимого отклонения
 (параметр экономически оправданной
уступки) критерия
(параметр экономически оправданной
уступки) критерия
 и находится максимальное значение
второго критерия
и находится максимальное значение
второго критерия
 при условии, что значение первого
критерия не должно отклоняться от своего
максимального значения более чем на
величину допустимой уступки, т.е. решатся
задача:
при условии, что значение первого
критерия не должно отклоняться от своего
максимального значения более чем на
величину допустимой уступки, т.е. решатся
задача:

Снова
назначается величина уступки
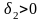 по второму критерию, которая вместе с
первой уступкой используется для
нахождения условного максимума третьего
частного критерия:
по второму критерию, которая вместе с
первой уступкой используется для
нахождения условного максимума третьего
частного критерия:
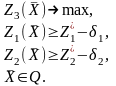
Аналогичные
процедуры повторяются до тех пор, пока
не будет выявлено максимальное значение
последнего по важности критерия
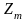 при условии, что значение каждого из
первых m-1
частных критериев отличается от
соответствующего условного максимума
не более чем на величину допустимой
уступки по данному критерию. Полученное
на последнем этапе решение считается
оптимальным. Следует заметить, что этот
метод не всегда приводит к эффективному
решению.
при условии, что значение каждого из
первых m-1
частных критериев отличается от
соответствующего условного максимума
не более чем на величину допустимой
уступки по данному критерию. Полученное
на последнем этапе решение считается
оптимальным. Следует заметить, что этот
метод не всегда приводит к эффективному
решению.
Пример. Решим задачу многокритериальной оптимизации методом последовательных уступок.
Решение.Пусть задача трехкритериальной оптимизации имеет вид
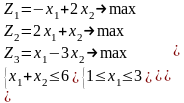
Заметим, что, так как коэффициенты при одних и тех же переменных в данных частных критериях имеют разные знаки, то в заданной области допустимых решений невозможно одновременно улучшить все частные критерии, т.е. в рассматриваемом случае область компромиссов (область Парето) совпадает с областью допустимых решений.
Для определенности будем считать, что допустимые уступки по первым двум критериям заданы:

Максимизируем функцию в области допустимых решений, т.е. решаем однокритериальную задачу. Это несложно сделать графическим методом решения ЗЛП (см. рис. 2).
Максимум функции достигается в точкеА области Q с координатами (1;4), так что в данном случае
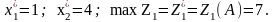
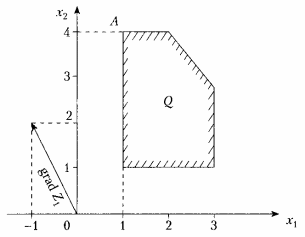
Рисунок 2. Решение однокритериальной задачи по критерию
Переходим
к максимизации функции
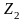 при тех же условиях и дополнительном
ограничении, позволяющем учесть, что
по критерию
нельзя уступать более чем на
при тех же условиях и дополнительном
ограничении, позволяющем учесть, что
по критерию
нельзя уступать более чем на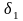 .
Так как в нашем примере
.
Так как в нашем примере
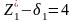 ,
то дополнительное ограничение будет
иметь вид:
,
то дополнительное ограничение будет
иметь вид:
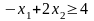 .
.
Задачу с новым ограничением также решаем графически (см. рис. 3).
Получаем,
что максимум функции
достигается в точкеВ
части
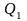 области Q,
так что
области Q,
так что
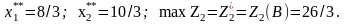
Теперь
уступаем по критерию
на величину уступки
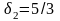 и получаем второе дополнительное
ограничение:
и получаем второе дополнительное
ограничение:

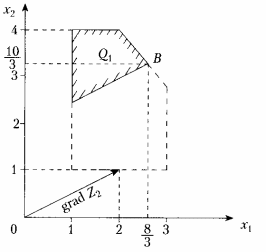
Рисунок 3. Решение однокритериальной задачи по критерию
Максимизируем
функцию
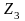 при условиях
при условиях
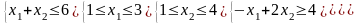
Решение этой задачи представлено на рисунке 4.
Таким образом, получаем оптимальное решение рассматриваемой трехкритериальной задачи в точкеС:
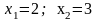 .
.
Соответствующие значения частных критериев при этом составляют:
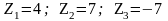 .
.
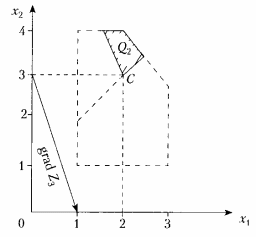
Рисунок 4. Решение однокритериальной задачи по критерию
Задачи для самостоятельного решения
Задание
1.Найти
компромиссное решение многокритериальной
задачи оптимизации методом последовательных
уступок и / или методом идеальной точки5.
При использовании метода последовательных
уступок принять величину экономически
оправданной уступки по первому критерию,
равной
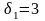 .
.
Варианты 1.1 – 1.10
|
|||
1.1 |
|
1.2 |
|
1.3 |
|
1.4 |
|
1.5 |
|
1.6 |
|
1.7 |
|
1.8 |
|
1.9 |
|
1.10 |
|
Раздел 4. Неотрицательные матрицы и модели Леонтьева
Рассмотрим применение матричного исчисления к задачам в экономической сфере, а именно, в межотраслевом балансе.
4.1. Некоторые сведения из линейной алгебры Собственные значения и собственные векторы неотрицательных матриц
Каждому
линейному оператору
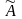 в данном базисе соответствует матрица
в данном базисе соответствует матрица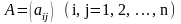 ,
которая называется матрицей
оператора[6].
С помощью матрицы оператора для любого
вектора х
можно найти его образ – вектор y,
используя матричное уравнение y
= Ax.Особую
роль в приложениях линейной алгебры
играют векторы, которые под воздействием
линейного оператора
,
которая называется матрицей
оператора[6].
С помощью матрицы оператора для любого
вектора х
можно найти его образ – вектор y,
используя матричное уравнение y
= Ax.Особую
роль в приложениях линейной алгебры
играют векторы, которые под воздействием
линейного оператора
 (матрицы
А)преобразуются
в новые векторы, коллинеарные
исходным.
Такие векторы получили название
собственных
векторов оператора
(матрицы
А),
а соответствующие им числа – собственных
значений оператора
(матрицы
А).
(матрицы
А)преобразуются
в новые векторы, коллинеарные
исходным.
Такие векторы получили название
собственных
векторов оператора
(матрицы
А),
а соответствующие им числа – собственных
значений оператора
(матрицы
А).
Определение
1. Вектор
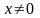 называется собственным
вектором
линейного оператора
(матрицы
А),
если найдется такое число
называется собственным
вектором
линейного оператора
(матрицы
А),
если найдется такое число
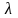 ,что
,что
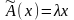
или в матричном виде
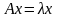 или
или
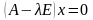 (1)
(1)
Число называется собственным значением (числом) оператора (матрицы А), соответствующим вектору х.Множество всех собственных значений оператора (матрицы А) называется спектром линейного оператора (матрицы А).
Уравнение (1) однородно и для существования его ненулевого решения необходимо и достаточно, чтобы определительматрицы системы равнялся нулю, т.е.
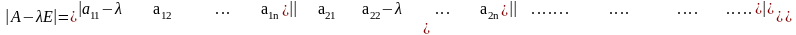 . (2)
. (2)
Определитель
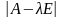 называется характеристическим
многочленом линейного оператора
(матрицы
А),
а уравнение (2) – его (ее) характеристическим
уравнением.
называется характеристическим
многочленом линейного оператора
(матрицы
А),
а уравнение (2) – его (ее) характеристическим
уравнением.
Собственные векторы и собственные значения неотрицательных матриц являются важными характеристиками функционирования экономических систем.
Определение
2. МатрицаА
называется неотрицательной
(положительной) и
обозначается
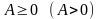 ,
если все ее элементы неотрицательны
(положительны).
,
если все ее элементы неотрицательны
(положительны).
Особое место среди неотрицательных матриц занимают неразложимые матрицы.
Определение 3. Неотрицательная квадратная матрицаАпорядка nназывается разложимой, если одновременной перестановкой строк и столбцов ее можно привести к виду
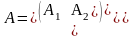 , (3)
, (3)
где
0 – нуль-матрица;
и
– квадратные матрицы размеров
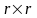 и
и
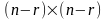 соответственно; в противном случае
матрица называется неразложимой.
соответственно; в противном случае
матрица называется неразложимой.
Примеры:
1.
Матрица
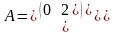 неразложима, так как перестановкой
первой и второй строки и первого и
второго столбца получим матрицу
неразложима, так как перестановкой
первой и второй строки и первого и
второго столбца получим матрицу
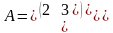 ,
которая не соответствует виду (3).
,
которая не соответствует виду (3).
2.
Матрица
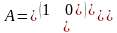 разложима, так как перестановкой первой
и второй строки и первого и второго
столбца получим матрицу
,
которая соответствует виду (3) разложимой
матрицы.
разложима, так как перестановкой первой
и второй строки и первого и второго
столбца получим матрицу
,
которая соответствует виду (3) разложимой
матрицы.
Замечания:
1. Любая положительная матрица неразложима.
2.
Квадратная матрицаА
размером
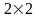 разложима тогда и только тогда, когда
либо
разложима тогда и только тогда, когда
либо
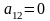 ,
либо
,
либо
 .Действительно,
если
,
то матрица А
уже приведена к виду (3). Если же
,
то меняя местами первую и вторую строки,
а затем первый и второй столбцы, получим
матрицу вида (3).
.Действительно,
если
,
то матрица А
уже приведена к виду (3). Если же
,
то меняя местами первую и вторую строки,
а затем первый и второй столбцы, получим
матрицу вида (3).
3.
С экономической точки зрения разложимость
матрицы говорит о том, что в рамках
данной экономической системы существует
некоторая автономная подсистема. Так,
если элемент
 матрицыА
показывает, какое количество продукции
i-ой
отрасли используется в j-ой
отрасли, то разложимость матрицы А
говорит о том, что существует группа
отраслей, не использующих продукцию
остальных отраслей. Неразложимость
матрицыА
показывает, что любая отрасль хотя бы
косвенным образом использует продукцию
всех отраслей экономической системы.
матрицыА
показывает, какое количество продукции
i-ой
отрасли используется в j-ой
отрасли, то разложимость матрицы А
говорит о том, что существует группа
отраслей, не использующих продукцию
остальных отраслей. Неразложимость
матрицыА
показывает, что любая отрасль хотя бы
косвенным образом использует продукцию
всех отраслей экономической системы.
Теорема Фробениуса – Перрона. Число и вектор Фробениуса, их свойства
Теорема
(Фробениуса-Перрона).
Неотрицательная матрицаА
имеет такое собственное значение
 ,
что
,
что
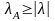 для любого собственного значения
матрицы
А.
Кроме
того, существует неотрицательный
собственный вектор
для любого собственного значения
матрицы
А.
Кроме
того, существует неотрицательный
собственный вектор
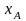 ,
соответствующий собственному числу
,
соответствующий собственному числу
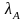 .
Причем, если А
неразложима, то
.
Причем, если А
неразложима, то
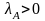 и существует
и существует
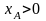 .
.
Определение
1. Собственное
значение
неотрицательной матрицыА
называется Фробениусовым
числом (числом Фробениуса),
а собственный вектор
 –
Фробениусовым
вектором (вектором Фробениуса)
матрицы А.
–
Фробениусовым
вектором (вектором Фробениуса)
матрицы А.
Для определения числа Фробениуса неотрицательной матрицыА необходимо решить уравнение (2), а затем среди корней (собственных значений ) выбрать максимальное неотрицательное значение. Вектор Фробениуса находят из уравнения (1), подставив в него вместо число Фробениуса .
Числа Фробениуса имеют ряд свойств, с которыми можно познакомиться в учебнике [2]. Одно из этих свойств дает простой способ определения числа Фробениуса матрицы: если все суммы элементов строк ( или столбцов) неотрицательной матрицы А равны одному и тому же числу , то число Фробениуса равно .
Пример. Пусть
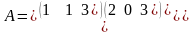 ;
;
 .
.
Тогда
=6,
так как суммы элементов каждого столбца
матрицыА
равны 6,
и
 =3,
так как суммы элементов каждой строки
матрицы В
равны 3.
=3,
так как суммы элементов каждой строки
матрицы В
равны 3.
Число и вектор Фробениуса используются в балансовых экономических моделях и, в частности, в модели международной торговли [6]. Так, равновесный вектор национального дохода в модели международной торговли является вектором Фробениуса структурной матрицы международного обмена. Кроме того, один из критериев продуктивности матрицы, которые будут рассмотрены ниже, формулируется в терминах числа Фробениуса[2].
4.2. Модель Леонтьева6 многоотраслевой экономики
Эффективное функционирование экономики предполагает наличие баланса между отдельными отраслями экономической системы. Каждая отрасль при этом выступает, с одной стороны, как производитель некоторой продукции, а с другой, как потребитель продуктов, вырабатываемых другими отраслями.
Цель балансового анализа – ответить на вопрос, возникающий в макроэкономике и связанный с эффективностью ведения многоотраслевого хозяйства: каким должен быть объем производства каждой из n отраслей, чтобы удовлетворить все потребности в продукции данной отрасли? Экономическая система, для которой применяется метод межотраслевого анализа, может быть большой (экономика страны) или малой (экономика региона или одного предприятия).
Для наглядного представления связи между отраслями экономической системы используют таблицы определенного вида, которые называют таблицами межотраслевого баланса (МОБ). Впервые эти таблицы были опубликованы в 1926 г. в СССР. Таблицы МОБ могут обеспечить органы власти и научно-исследовательские организации детализированной информацией о структурных пропорциях и межотраслевых связях в экономике страны, необходимой для прогнозирования и принятия решений в области экономической политики.
Различают отчетный и плановый межотраслевые балансы. Отчетный межотраслевой баланс отражает структуру производства и потребления продукции, произведенной в стране за отчетный год. Плановый межотраслевой баланс предназначен для планирования производства валового внутреннего продукта. В СССР такой план разрабатывался Госпланом и являлся директивным. В некоторых странах с рыночной экономикой, например, в Японии и Франции, такой план разрабатывается, но является индикативным, то есть не обязательным, а нацеливающим субъектов экономики на рациональные с точки зрения общества действия.
В советское время таблицымежотраслевого баланса разрабатывались в нашей стране на регулярной основе с 1959 по 1987 год. Первые плановые межотраслевые балансы в стоимостном и натуральном выражении были построены в 1962 г. Далее работы были распространены на республики и регионы. По данным за 1966 г. межотраслевые балансы были построены по всем союзным республикам и экономическим районам РСФСР. Последние базовые таблицы "затраты – выпуск" были разработаны за 1995 год. Дело в том, что номенклатуры отраслей и продукции в этих таблицах базировались на действующем в тот момент Общероссийском классификаторе отраслей народного хозяйства, который на сегодняшний день устарел.
14 февраля 2009 года, вышло распоряжение Правительства России №201-р, которое предписывало Росстату разработать базовые таблицы «затраты – выпуск» за 2011 год, в 2015 году представить их в Правительство Российской Федерации и осуществлять разработку базовых таблиц «затраты – выпуск» на регулярной основе 1 раз в 5 лет. Таблицы должны разрабатываться в соответствии с международными стандартами, изложенными в руководствах по составлению таблиц "затраты – выпуск" ООН и Евростата, и с учетом особенностей российской информационной базы.
Математическая модель межотраслевого баланса, допускающая широкие возможности анализа, планирования и прогнозирования хозяйственной деятельности, появилась в 1936 г. в трудах известного экономиста В.В. Леонтьева [6]. Предложенная Леонтьевым алгебраическая теория анализа «затраты – выпуск» сводилась ксистеме линейных уравнений, в которых параметрами были коэффициенты затрат на производство продукции. Леонтьев показал, что коэффициенты, выражающие отношения между секторами экономики (коэффициенты текущих материальных затрат), могут быть оценены статистически, что они достаточно устойчивы и их можно прогнозировать; обосновал существование наиболее важных коэффициентов, изменения которых необходимо отслеживать в первую очередь. Относительная простота измерений определила большие аналитические и прогностические возможности метода «затраты – выпуск».
Рассмотрим наиболее простой вариант модели межотраслевого баланса. Предположим, что весь производственный сектор народного хозяйства разбит на n чистых отраслей. Чистая отрасль – это условное понятие, которое определяет некоторую часть народного хозяйства, более или менее цельную (например, энергетика, машиностроение, сельское хозяйство и т.п.).
Пусть
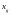 –
количество продукции i-ой
отрасли, расходуемое на производство
продукции j-ой
отрасли (межотраслевые
поставки, материальные затраты),
–
количество продукции i-ой
отрасли, расходуемое на производство
продукции j-ой
отрасли (межотраслевые
поставки, материальные затраты),
 –
объем производства i-ой
отрасли за данный промежуток времени
–валовой
выпуск продукции,
–
объем производства i-ой
отрасли за данный промежуток времени
–валовой
выпуск продукции,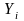 – объем потребления продукции i-ой
отрасли в непроизводственной сфере –
объем
конечного потребления,
– объем потребления продукции i-ой
отрасли в непроизводственной сфере –
объем
конечного потребления,
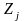 – условно чистая продукция, которая
включает оплату труда, чистый доход и
амортизационные отчисления, идущие на
возмещение выбытия основных фондов.
– условно чистая продукция, которая
включает оплату труда, чистый доход и
амортизационные отчисления, идущие на
возмещение выбытия основных фондов.
Единицы измерения всех указанных величин могут быть натуральными (кубометры, тонны, штуки и т.п.) или стоимостными. В зависимости от этого различают натуральный и стоимостной межотраслевые балансы. Мы будем рассматривать стоимостной баланс.
В таблице 1 отражена принципиальная схема межотраслевого баланса в стоимостном выражении. Каждая отрасль представлена двояким образом: как элемент строки, она выступает в роли производителя продукции, а как элемент столбца – в роли потребителя продукции своей и других отраслей. Заметим, что таблица МОБ состоит из четырех частей (квадрантов), имеющих различное экономическое содержание.
Первый квадрант МОБ – это важнейшая часть межотраслевого баланса, содержащая информацию о межотраслевых связях.
Таблица 1 – Общая схема межотраслевого баланса производства и распределения продукции
Производящие отрасли |
Потребляющие отрасли |
Итого |
Конечный продукт |
Валовой продукт |
|||||||||
1 |
2 |
… |
j |
… |
n |
||||||||
1 |
|
|
… |
|
… |
|
|
|
|
||||
2 |
|
|
… |
|
… |
|
|
|
|
||||
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
||||
i |
|
|
|
|
|
|
|
|
|
||||
… |
… |
… |
I квадрант |
… |
… |
II квадрант
|
|||||||
n |
|
|
… |
|
… |
|
|
|
|
||||
Итого |
|
|
… |
|
|
|
|
|
|
||||
Условно чистая продукция |
|
|
… |
|
… |
|
|
IV квадрант |
|||||
|
|
|
III квадрант
|
|
|||||||||
Валовой продукт |
|
|
… |
|
… |
|
|
||||||
Основная часть этого квадранта представлена межотраслевыми поставками . При этом межотраслевые поставки в каждой i-ой строке (текущее производственное потребление) показывают, сколько продукции, произведенной i-ой отраслью, потребляется всеми другими отраслями экономической системы, включая i-ую. Межотраслевые поставки в каждом j-ом столбце (текущие производственные затраты) – это потребляемое j-ой отраслью количество продукции, произведенной всеми отраслями, включая j-ую. Последний столбец и последняя строка первого квадранта представляют соответственно суммарное текущее производственное потребление продукции отрасли i всеми отраслями исуммарные текущие производственные затраты всех отраслей на производство продукции отрасли j. Нетрудно убедиться в том, что суммы элементов последнего столбца и последней строки I квадранта состоят из одних и тех же слагаемых и поэтому равны между собой. Это общее значение представлено в правом нижнем углу I квадранта. Оно называется промежуточным продуктом экономической системы и означает, что суммарное текущее производственное потребление равно суммарным текущим производственным затратам.
Второй квадрант состоит из двух столбцов. Первый из них – столбец конечной продукции всех отраслей , то есть продукции, выходящей из сферы производства в область конечного личного и общественного потребления, не идущего на текущие производственные нужды. Во втором столбце представлены объемы валовой продукции отраслей
Квадранты I иII отражают баланс между производством и потреблением.
Третий квадрант представлен двумя строками: строкой условно чистой продукции и строкой объемов валовой продукции отраслей .
Первый и третий квадранты отражают стоимостную структуру продукции каждой отрасли (или стоимостную структуру национального дохода).
Четвертый квадрант непосредственного отношения к сфере производства не имеет, поэтому он не содержит никаких значений. По сути, этот квадрант должен отражать,как полученные в сфере материального производства первичные доходы населения (заработная плата, личные доходы и пр.), государства (налоги, прибыль и пр.), предприятий перераспределяются через различные каналы (финансово-кредитную систему, сферу обслуживания, общественно-политические организации и т.д.), в результате чего образуются конечные доходы населения, государства и т.д.
Переходим к построениюлинейной балансовой модели (ЛБМ) Леонтьева. Она представляет собой систему линейных уравнений, каждое из которых отражает равенство (баланс) между продукцией, производимой отдельной экономической отраслью, и совокупной потребностью в этой продукции во всей экономической системе.
Рассматривая схему МОБ по столбцам, можно сделать очевидный вывод, что сумматекущих производственных затрат любой потребляющей отрасли и ее условно чистой продукции равна валовой продукции этой отрасли. Данный вывод можно записать в виде соотношения:
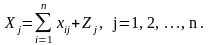 (1)
(1)
Рассматривая схему МОБ по строкам для каждой производящей отрасли, можно видеть, что валовая продукция той или иной отрасли равна сумме текущего производственного потребления ее продукциивсеми отраслями и конечной продукции данной отрасли:
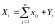 ,i
= 1,2, …, n
(2)
,i
= 1,2, …, n
(2)
Просуммируем по всем отраслям системы (1) и (2), получим
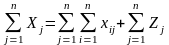 ,
,
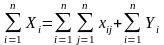 .
.
Левые части двух равенств одинаковы, так как представляют собой весь валовой общественный продукт. Первые слагаемые правых частей также равны. Как было отмечено ранее, это величинапромежуточного продукта экономической системы.Балансовый характер таблицы МОБ выражается в том, что из равенства уже обозначенных сумм вытекает очевидное равенство суммарной конечной и суммарной условно чистой продукции, то есть
 .
.
Для получения ЛБМ продолжим работу с системой (2),представив ее в развернутом виде
( 2')
2')
Основу экономико-математической модели МОБ составляет матрица коэффициентов прямыхвнутрипроизводственных затрат (матрица технологическихкоэффициентов)А=(aij).
Определение 1. Коэффициенты прямых внутрипроизводственных затрат aijпоказывают, какое количество продукции i-ой отрасли необходимо (если учитывать только прямые затраты) для производства единицы валовой продукцииj-ой отрасли, то есть
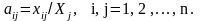 (3)
(3)
Из равенства (3) получаем
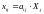 .
(4)
.
(4)
Для получения значений в реальной экономике можно использовать два способа:
1. Статистический. Коэффициенты определяются на основе анализа отчетных балансов за прошлые годы. Неизменность во времени коэффициентов прямых затрат в этом случае достигается подходящим выбором отраслей межотраслевого баланса. Как показывает практика, при правильном выборе достаточно крупных отраслей коэффициенты оказываются достаточно устойчивыми.
2. Нормативный. Строится модель отрасли межотраслевого баланса. В этой модели отрасль рассматривается как совокупность отдельных производств, для каждого из которых уже разработаны нормативы затрат. Если заранее знать, какую продукцию будут выпускать производства отрасли, то по нормативам затрат можно рассчитать среднеотраслевые коэффициенты прямых затрат.
Заменив все межотраслевые поставки в системе (2') в соответствии с равенствами (4), получим линейную балансовую модель Леонтьева вида
(5)
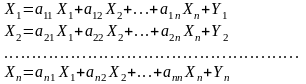
или в матричной форме
X = AX + Y. (6)
С помощью этой модели можно выполнять три вида плановых расчетов:
1. Задав в модели величины валовой продукции каждой отрасли Xi, можно определить объемы конечной продукции каждой отрасли Yiпо формуле
Y
= (E
- A)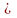 X.
(7)
X.
(7)
2. Задав величины конечной продукции всех отраслей Yi, можно определить величины валовой продукции каждой отрасли Xiпо формуле
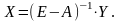 (8)
(8)
3. Для ряда отраслей задав величины валовой продукции, а для всех остальных отраслей задав объемы конечной продукции, можно найти недостающие величины конечной продукции первых отраслей и объемы валовой продукции вторых.
В
формулах (7) и (8) Е
обозначает единичную матрицу n-го
порядка, а (Е
– А)-1
обозначает матрицу, обратную к матрице
(Е
- А).
Если определитель матрицы (Е
- А)отличен
от нуля, т.е. эта матрица невырожденная,
то обратная к ней матрица существует.
Обозначим эту обратную матрицу через
 .Тогда
систему уравнений в матричной форме
(8) можно записать в виде
.Тогда
систему уравнений в матричной форме
(8) можно записать в виде
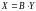 .
.
Определение
2.
Элементы матрицы
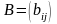 называются коэффициентами
полных материальных затрат.
Они показывают, сколько всего нужно
произвести продукции i-ой
отрасли для выпуска единицыконечной
продукцииj-ой
отрасли.
называются коэффициентами
полных материальных затрат.
Они показывают, сколько всего нужно
произвести продукции i-ой
отрасли для выпуска единицыконечной
продукцииj-ой
отрасли.
Из экономического смысла векторов Х иYследует неотрицательность их координат. Вопрос о положительной разрешимости уравнения (6) зависит от свойств матрицы А. Плановые расчеты по модели Леонтьева можно выполнять, если матрица А является продуктивной.
Определение3. Неотрицательная матрицаА называется продуктивной, если существует такой неотрицательный вектор Х 0, что
Х >АХ. (9)
Неравенство
(9) означает, что для выпуска каждого
вида продукта потребуется затрат меньше,
чем стоит сам продукт. Очевидно, что
условие (9) означает существование
положительного вектора конечной
продукции
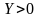 для модели межотраслевого баланса (6).
для модели межотраслевого баланса (6).
Для того чтобы матрица коэффициентов прямых материальных затратА была продуктивной, необходимо и достаточно, чтобы выполнялось одно из перечисленных ниже условий:
1) матрица (Е - А) неотрицательно обратима, т.е. существует обратная матрицаВ=(Е – А)-1 , состоящая из неотрицательных элементов;
2)
матричный рядЕ
+ А+ А2
+ А3
+
...=
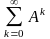 сходится, причем его сумма равна обратной
матрице В=
сходится, причем его сумма равна обратной
матрице В=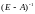 ;
;
3)
наибольшее по модулю собственное
значение
матрицыА,
то есть решение характеристического
уравнения
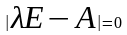 ,
строго меньше единицы. Нетрудно
догадаться, что
– это число Фробениуса
матрицы А.
Тогда получаем еще один простой способ
проверки продуктивности (правда, это
только достаточный признак продуктивности)
матрицы А:
если наибольшая из сумм элементов
матрицы в каждом столбце (или строке)
строго меньше единицы, то матрица
продуктивна7
[6], [7].
,
строго меньше единицы. Нетрудно
догадаться, что
– это число Фробениуса
матрицы А.
Тогда получаем еще один простой способ
проверки продуктивности (правда, это
только достаточный признак продуктивности)
матрицы А:
если наибольшая из сумм элементов
матрицы в каждом столбце (или строке)
строго меньше единицы, то матрица
продуктивна7
[6], [7].
4) все главные миноры матрицы (Е – А), т.е. определители подматриц, образованных элементами первыхk строк и первых kстолбцов этой матрицы, порядка от 1 до п, положительны.
Рассмотрим другое определение коэффициентов полных материальных затрат, исходя из того, что кроме прямых затрат на получение той или иной продукции существуют косвенные затраты. Косвенные затраты относятся к предшествующим стадиям производства и входят в продукт не прямо, а через другие средства производства (см. рис. 1).
Определение
4.
Коэффициентами полных материальных
затрат
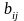 называется
сумма прямых
и косвенных
затрат
продукции
называется
сумма прямых
и косвенных
затрат
продукции
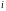 -й
отрасли для производства единицы
продукции
-й
отрасли для производства единицы
продукции
 -й
отрасли через все промежуточные продукты
на всех предшествующих стадиях
производства.
-й
отрасли через все промежуточные продукты
на всех предшествующих стадиях
производства.
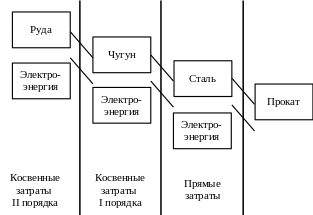
Рисунок 1. Прямые и косвенные затраты на производство проката
Коэффициенты косвенных затрат связаны с коэффициентами прямых и полных затрат формулами
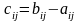 .
.
Примеры решения задач
Пример 1. Рассматривается двухотраслевая модель экономики, заданная балансовой таблицей
Производящие отрасли |
Потребляющие отрасли |
Конечный продукт |
||
Энергетика |
Машиностроение |
|||
Энергетика |
3 |
7 |
4 |
|
Машиностроение |
6 |
5 |
4 |
|
Определить:
1. Валовой выпуск продукции каждой отрасли .
2. Матрицу коэффициентов прямых внутрипроизводственных затрат А.
3. Построить линейную балансовую модель Леонтьева.
4. Матрицу коэффициентов полных затрат В.
5. Является ли матрицаА продуктивной? Для ответа на вопрос используйте хотя бы два критерия.
Все расчетные значения округлите до трех знаков после запятой.
Решение:
1. Валовой выпуск продукции каждой отрасли определяем как сумму элементов каждой строки балансовой таблицы:
для
энергетики –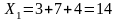
для
машиностроения –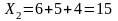
2. Элементы матрицыАкоэффициентов прямых внутрипроизводственных затрат определяем по формуле
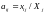 i,j
= 1, 2, …, n;
i,j
= 1, 2, …, n;
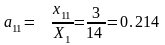 ,
,
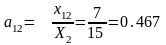 ,
,
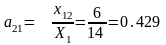 ,
,
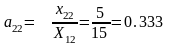 .
.
Таким образом, получаем матрицу коэффициентов прямых внутрипроизводственных затрат
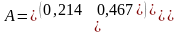 .
.
3. Линейная балансовая модель Леонтьева имеет вид:
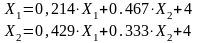
4. Матрицу коэффициентов полных затратВнаходим по формуле
,
где Е – единичная матрица второго порядка, т.е.
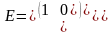 .
.
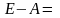
 -
-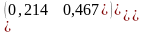 =
=
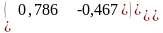 .
.
Далее действуем в соответствии с порядком определения обратной матрицы:
1)
определитель

2)
транспонированная матрица
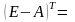
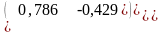 .
.
3)
присоединенную матрицу получаем из
алгебраических дополнений к элементам
транспонированной, например,
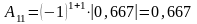 .
Присоединенная матрица имеет вид
.
Присоединенная матрица имеет вид
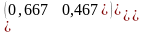 .
.
4) обратная матрица, т.е. матрица коэффициентов полных затрат
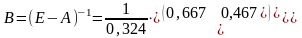 =
=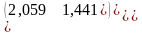 8.
8.
5. МатрицаА является продуктивной, так как выполняются, например, условия продуктивности 1 и 3:
1) обратная матрица (Е – А)-1 0, т.к. все ее элементы неотрицательны;
3) наибольшая из сумм элементов столбцов матрицыА равна 0,8, что меньше единицы.
Пример 2. Промышленная группа предприятий (холдинг) выпускает продукцию трех видов, при этом каждое из трех предприятий группы специализируется на выпуске продукции одного вида. Часть выпускаемой продукции потребляется предприятиями холдинга (идет на внутреннее потребление), остальная часть поставляется за его пределы (внешним потребителям) и является конечным продуктом. Специалистами управляющей компании получены экономические оценки (i=1,2,3; j=1,2,3) элементов технологической матрицыА(норм расхода, коэффициентов прямых материальных затрат) и элементов вектора конечной продукции Y, которые приведены в таблице.
Производящие отрасли |
Коэффициенты прямых затрат |
Конечный продукт |
||
Отрасль 1 |
Отрасль 2 |
Отрасль 3 |
||
Отрасль 1 |
0,1 |
0,1 |
0,2 |
160 |
Отрасль 2 |
0,1 |
0,2 |
0,3 |
180 |
Отрасль 3 |
0,1 |
0,2 |
0,3 |
170 |
Требуется:
Проверить продуктивность технологической матрицы А=( ) (матрицы коэффициентов прямых внутрипроизводственных затрат).
Построить линейную балансовую модель Леонтьева и таблицу межотраслевого баланса производства и распределения продукции предприятий холдинга, определив для каждой отрасли валовой выпуск, межотраслевые поставки продукции, условно чистую продукцию.
Все расчетные значения округлите до трех знаков после запятой.
Решение:
1. Проверка продуктивности технологической матрицы А=( ):
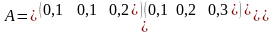 ,
,
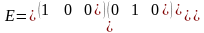 ,
,
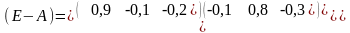 ,
,
 9.
9.
Вывод:
так как все элементы матрицы
 неотрицательны и сумма элементов всех
трех столбцов матрицыА
меньше единицы, то матрица А
продуктивна.
неотрицательны и сумма элементов всех
трех столбцов матрицыА
меньше единицы, то матрица А
продуктивна.
2. Построение баланса производства и распределения продукции предприятий холдинга:
1) линейная балансовая модель Леонтьева имеет вид
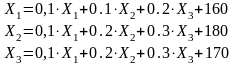
2) валовой выпуск каждого предприятия находим по формуле
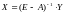 .
.
Выполняем умножение матриц
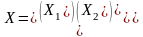
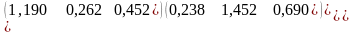 =
=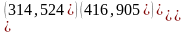 ;
;
3) межотраслевые поставки продукции определяем по формуле
 ;
;
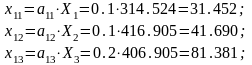
и т.д.
4) условно чистую продукцию находим из равенств
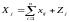
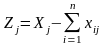 ;
;
5) строим таблицу межотраслевого баланса
Производящие отрасли |
Потребляющие отрасли |
Суммы |
Конечный продукт |
Валовой продукт |
|||||
Отрасль 1 |
Отрасль 2 |
Отрасль 3 |
|||||||
Отрасль 1 |
31,452 |
41,690 |
81,381 |
154,524 |
160 |
314,524 |
|||
Отрасль 2 |
31,452 |
83,381 |
122,071 |
236,905 |
180 |
416,905 |
|||
Отрасль 3 |
31,452 |
83,381 |
122,071 |
236,905 |
170 |
406,905 |
|||
Суммы |
94,357 |
208,452 |
325,524 |
628,333 |
510 |
1138,33 |
|||
Условно чистая продукция |
220,167 |
208,452 |
81,381 |
510 |
|
||||
Валовой продукт |
314,524 |
416,905 |
406,905 |
1138,33 |
|||||
Замечание. Баланс составлен правильно, еслиполучены следующие равенства:
1)Суммарное текущее производственное потребление равно суммарным текущим производственным затратам.Это промежуточный продукт экономической системы. В нашем случае он равен 628,333.
2) Суммарный конечный продукт равен суммарной условно чистой продукции.В нашем примере это общее значение равно 51010.
Задачи для самостоятельного решения
Задание 1.Рассматривается многоотраслевая модель экономики, заданная балансовой таблицей.
Определить:
1. Валовой выпуск продукции каждой отрасли .
2. Матрицу коэффициентов прямых внутрипроизводственных затрат А.
3. Построить линейную балансовую модель Леонтьева.
4. Матрицу коэффициентов полных затрат В.
5. Является ли матрицаА продуктивной? Для ответа на вопрос используйте хотя бы два критерия.
Все расчетные значения округлите до трех знаков после запятой.
Варианты 1.1 – 1.10
Вариант 1.1 – Балансовая таблица
Производящие отрасли |
Потребляющие отрасли |
Конечный продукт |
||
Отрасль 1 |
Отрасль 2 |
|||
Отрасль 1 |
7 |
21 |
72 |
|
Отрасль 2 |
12 |
15 |
123 |
|
Вариант 1.2 – Балансовая таблица
Производящие отрасли |
Потребляющие отрасли |
Конечный продукт |
||
Отрасль 1 |
Отрасль 2 |
|||
Отрасль 1 |
100 |
160 |
240 |
|
Отрасль 2 |
275 |
40 |
85 |
|
Вариант 1.3 – Балансовая таблица
Производящие отрасли |
Потребляющие отрасли |
Конечный продукт |
||
Отрасль 1 |
Отрасль 2 |
|||
Отрасль 1 |
80 |
120 |
300 |
|
Отрасль 2 |
70 |
30 |
200 |
|
Вариант 1.4 – Балансовая таблица
Производящие отрасли |
Потребляющие отрасли |
Конечный продукт |
||
Отрасль 1 |
Отрасль 2 |
Отрасль 3 |
||
Отрасль 1 |
50 |
60 |
80 |
60 |
Отрасль 2 |
25 |
90 |
40 |
25 |
Отрасль 3 |
25 |
60 |
40 |
35 |
Вариант 1.5 – Балансовая таблица
Производящие отрасли |
Потребляющие отрасли |
Конечный продукт |
||
Отрасль 1 |
Отрасль 2 |
Отрасль 3 |
||
Отрасль 1 |
10 |
5 |
15 |
70 |
Отрасль 2 |
15 |
15 |
10 |
60 |
Отрасль 3 |
5 |
10 |
20 |
65 |
Вариант 1.6 – Балансовая таблица
Производящие отрасли |
Потребляющие отрасли |
Конечный продукт |
||
Отрасль 1 |
Отрасль 2 |
Отрасль 3 |
||
Отрасль 1 |
40 |
18 |
25 |
21 |
Отрасль 2 |
16 |
9 |
25 |
16 |
Отрасль 3 |
80 |
45 |
50 |
75 |
Вариант 1.7 – Балансовая таблица
Производящие отрасли |
Потребляющие отрасли |
Конечный продукт |
||
Отрасль 1 |
Отрасль 2 |
Отрасль 3 |
||
Отрасль 1 |
18 |
36 |
25 |
1 |
Отрасль 2 |
45 |
90 |
25 |
20 |
Отрасль 3 |
36 |
36 |
50 |
30 |
Вариант 1.8 – Балансовая таблица
Производящие отрасли |
Потребляющие отрасли |
Конечный продукт |
||
Отрасль 1 |
Отрасль 2 |
Отрасль 3 |
||
Отрасль 1 |
0 |
37 |
0 |
200 |
Отрасль 2 |
47 |
0 |
40 |
100 |
Отрасль 3 |
0 |
19 |
79 |
300 |
Вариант 1.9 – Балансовая таблица
Производящие отрасли |
Потребляющие отрасли |
Конечный продукт |
|
Отрасль 1 |
Отрасль 2 |
||
Отрасль 1 |
15 |
60 |
25 |
Отрасль 2 |
25 |
5 |
20 |
Вариант 1.10 – Балансовая таблица
Производящие отрасли |
Потребляющие отрасли |
Конечный продукт |
|
Отрасль 1 |
Отрасль 2 |
||
Отрасль 1 |
5 |
60 |
35 |
Отрасль 2 |
25 |
5 |
20 |
Отрасль 3 |
50 |
10 |
- |
Задание 2.Промышленная группа предприятий (холдинг) выпускает продукцию трех видов, при этом каждое из трех предприятий группы специализируется на выпуске продукции одного вида. Часть выпускаемой продукции потребляется предприятиями холдинга (идет на внутреннее потребление), остальная часть поставляется за его пределы (внешним потребителям) и является конечным продуктом. Специалистами управляющей компании получены экономические оценки (i=1, 2, 3; j=1, 2, 3) элементов технологической матрицыА(норм расхода, коэффициентов прямых материальных затрат) и элементов вектора конечной продукции Y.
В соответствии с номером Вашего варианта выберите в таблице 1 числовые значения для таблицы 2.
Варианты 2.1 – 2.10
Таблица 1 – Данные по вариантам
Вариант |
Для первой строки |
Для второй строки |
Для третьей строки |
|||||||||
1А |
2А |
3А |
4А |
1Б |
2Б |
3Б |
4Б |
1В |
2В |
3В |
4В |
|
2.1 |
0,3 |
0,4 |
0,1 |
200 |
0,1 |
0,2 |
0,4 |
300 |
0,3 |
0,4 |
0,1 |
200 |
2.2 |
0,1 |
0,2 |
0,4 |
100 |
0,0 |
0,4 |
0,1 |
200 |
0,1 |
0,3 |
0,4 |
100 |
2.3 |
0,0 |
0,4 |
0,1 |
160 |
0,4 |
0,1 |
0,0 |
180 |
0,3 |
0,0 |
0,1 |
150 |
2.4 |
0,4 |
0,2 |
0,3 |
180 |
0,2 |
0,1 |
0,0 |
200 |
0,2 |
0,1 |
0,0 |
160 |
2.5 |
0,1 |
0,2 |
0,1 |
200 |
0,2 |
0,1 |
0,0 |
150 |
0,1 |
0,2 |
0,3 |
250 |
2.6 |
0,0 |
0,1 |
0,2 |
180 |
0,1 |
0,2 |
0,1 |
200 |
0,2 |
0,1 |
0,2 |
200 |
2.7 |
0,2 |
0,1 |
0,2 |
150 |
0,0 |
0,1 |
0,2 |
180 |
0,1 |
0,0 |
0,1 |
100 |
2.8 |
0,1 |
0,0 |
0,1 |
100 |
0,1 |
0,0 |
0,2 |
300 |
0,2 |
0,1 |
0,0 |
160 |
2.9 |
0,2 |
0,3 |
0,0 |
120 |
0,3 |
0,1 |
0,2 |
250 |
0,1 |
0,0 |
0,3 |
180 |
2.10 |
0,1 |
0,1 |
0,2 |
160 |
0,1 |
0,2 |
0,3 |
180 |
0,2 |
0,2 |
0,3 |
170 |
Таблица 2 – Формат данных задачи
Предприятия (виды продукции) |
Коэффициенты прямых затрат |
Конечный продуктY |
||
1 |
2 |
3 |
||
1 |
1А |
2А |
3А |
4А |
2 |
1Б |
2Б |
3Б |
4Б |
3 |
1В |
2В |
3В |
4В |
Требуется:
Проверить продуктивность технологической матрицы А=( ) (матрицы коэффициентов прямых внутрипроизводственных затрат).
Построить линейную балансовую модель Леонтьева и таблицу межотраслевого баланса производства и распределения продукции предприятий холдинга, определив для каждой отрасли валовой выпуск, межотраслевые поставки продукции, условно чистую продукцию.
Все расчетные значения округлите до трех знаков после запятой.
Рекомендуемая литература
а) основная:
1. Гармаш А.Н., Орлова И.В. Математические методы в управлении: Учеб.пособие. – М.: Вузовский учебник: ИНФРА-М, 2012.
ЭБС «Znanium.com»: https://www.znanium.com
2. Методы оптимальных решений в экономике и финансах: учебник/коллектив авторов; под ред. В.М. Гончаренко, В.Ю. Попова. – М.: КНОРУС, 2014, 2016. – 400 с.
ЭБС «Book.ru»: https://www.book.ru/book/915989
3. Орлова И.В., Половников В.А. Экономико-математические методы и модели: компьютерное моделирование: Учеб.пособие. – 3-е изд., перераб. и доп. – М.: Вузовский учебник: ИНФРА-М, 2012, 2014.
ЭБС «Znanium.com»: https://www.znanium.com
б) дополнительная:
4.Кремер Н.Ш. и др. Исследование операций в экономике: Учебник для вузов. – М.: Издательство ЮРАЙТ, 2014, 2016. – Серия: Бакалавр. Академический курс.
ЭБС «Biblio-online.ru»: https://www. biblio-online.ru
5. Орлова И.В. Экономико-математическое моделирование: Практическое пособие по решению задач. – 2-е изд., испр. и доп. – М.: Вузовский учебник: ИНФРА-М, 2012–2014.
ЭБС «Znanium.com»: https://www.znanium.com
6. Орлова И.В. Линейная алгебра и аналитическая геометрия для экономистов: учебник и практикум для прикладного бакалавриата / И.В. Орлова, В.В. Угрозов, Е.С. Филонова. – М.: Издательство Юрайт, 2014, 2015.
ЭБС «Biblio-online.ru»: https://www. biblio-online.ru
7. Экономико-математические методы и прикладные модели: учебник для бакалавриата и магистратуры / В.В. Федосеев, А.Н. Гармаш, И.В. Орлова; под ред. В.В. Федосеева. – 4-е изд. перераб. и доп. – М.: Издательство Юрайт, 2016.
ЭБС «Biblio-online.ru»: https://www. biblio-online.ru
Е.С. Филонова линейные модели в экономике Учебное пособие
Для студентов, обучающихся по направлениям подготовки
«Экономика», «Менеджмент», «Бизнес-информатика»
(программа подготовки бакалавра)
Подписано в печать 22.07.2016 г. Формат 60х84 1/16
Печать ризография. Бумага офсетная. Гарнитура Times
7,75Усл. Печ. Л. Тираж 500 экз. Заказ № 225
Лицензия ПД № 8-0023 от 25.09.2000 г.
Отпечатано с готового оригинал-макета
в ООО Полиграфическая фирма «Картуш»
г. Орел, ул. 2-я Посадская, 26. Тел./факс (4862) 44-51-46.
E-mail: kartush@orel.ruwww.kartush-orel.ru
1Теоремы 1 – 2 допускают обобщение на случай n переменных [4].
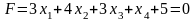
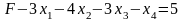
2В целевой функции задачи кроме слагаемых с переменными может быть свободный член, например, . Тогда в равенстве справабудет не нулевое значение, а этот свободный член, то есть , который появится вместо нуля в первой симплексной таблице на пересечении строки F и столбца «Свободный член».
3 Если в задаче ЛП две переменные, то метод Гомори можно реализовать и графически.
4 Для двоичных переменных используются альтернативные названия: «бинарные переменные», «булевы переменные».
5 Решение многокритериальной задачи оптимизации методом идеальной точки рассмотрено в размещенном на портале Финансового университета учебно-методическом пособии:
Александрова А.И., Гончаренко В.М. Методы оптимальных решений. Методические указания для выполнения контрольных работ. 2015 г.
6 В литературе используются и другие названия данной модели: модель межотраслевого баланса, модель «затраты – выпуск».
7 С экономической точки зрения сумму элементов столбца матрицыА можно трактовать как суммарные затраты всех отраслей на выпуск единицы продукции данной отрасли. Если эти затраты меньше единицы, то отрасль рентабельна. Если все отрасли рентабельны (сумма элементов любого столбца матрицыА меньше единицы), то матрица А продуктивна. При этом, чем ниже общий уровень коэффициентов матрицыА, тем меньше наибольшее по модулю собственное значение и выше продуктивность.
8 Действия с матрицами, в том числе определение обратной матрицы, можно осуществлять с использованием математических функций, встроенных в Excel[3], [6].
9 В данном примере мы опустили процедуру нахождения обратной матрицы. Напомним лишь, что определитель третьего порядка можно вычислить по правилу треугольника.
10 Для получения более точных результатов рекомендуется не округлять значения в промежуточных расчетах.