
- •Е.С. Филонова линейные модели в экономике Учебное пособие
- •Орел 2016
- •Рецензент:
- •Орлова и.В.
- •Содержание
- •Предисловие
- •Введение. Понятие, роль и этапы математического моделирования в экономике и финансах
- •Раздел1. Основы линейного программирования
- •1.1. Экономико-математическая модель оптимизационной задачи и задачи линейного программирования
- •1.2. Графический метод решения задачи линейного программирования
- •1.3. Симплекс-метод решения задач линейного программирования
- •1.4. Основы теории двойственности
- •Задачи для самостоятельного решения
- •Раздел 2. Специальные задачи линейного программирования
- •2.1. Задачи дискретного программирования
- •2.2.Транспортная задача. Методы построения опорного плана. Улучшение плана методом потенциалов
- •2 Этап.Построение системы потенциалов и проверка начального плана на оптимальность
- •Задачи для самостоятельного решения
- •Раздел 3. Задачи многокритериальной оптимизации
- •3.1. Происхождение и постановка задачи многокритериальной оптимизации
- •3.2. Основные методы решения многокритериальных задач
- •Задачи для самостоятельного решения
- •Раздел 4. Неотрицательные матрицы и модели Леонтьева
- •4.1. Некоторые сведения из линейной алгебры Собственные значения и собственные векторы неотрицательных матриц
- •Теорема Фробениуса – Перрона. Число и вектор Фробениуса, их свойства
- •4.2. Модель Леонтьева6 многоотраслевой экономики
- •Задачи для самостоятельного решения
- •Рекомендуемая литература
- •Е.С. Филонова линейные модели в экономике Учебное пособие
- •7,75Усл. Печ. Л. Тираж 500 экз. Заказ № 225
Раздел1. Основы линейного программирования
1.1. Экономико-математическая модель оптимизационной задачи и задачи линейного программирования
Оптимизационные задачи возникают при практической реализации принципа оптимальности в управлении.
Принцип оптимальности состоит в выборе среди множества допускаемых в данной ситуации решений наиболее выгодного с точки зрения критерия оптимальности.
Примеры критериев оптимальности:
1) максимум прибыли;
2)минимум затрат (материальных ресурсов, времени, стоимости и т.д.);
3)максимальное число комплектов продукции и т.д.
Экономико-математическая модель оптимизационной задачи:
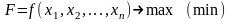 (1)
(1)
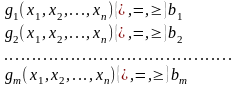
 (2)
(2)
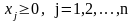 (3)
(3)
Основные элементымодели:
Целевая функция (1) – отражает критерий оптимальности.
Система функциональных ограничений(2) – составляется из условий задачи.
Система прямых ограничений (3) – обеспечивает допустимость искомого решения.
Любая оптимизационная задача имеет два вида решений:
допустимые;
оптимальные.
Определение
1. Допустимым решением
оптимизационной задачи называется
такой набор значений переменных
 ,
при котором выполняются все условия
систем (2) и (3).
,
при котором выполняются все условия
систем (2) и (3).
Определение 2. Допустимое решение будет оптимальным, если на нем целевая функция (1) достигает своего максимума или минимума.
Большой класс оптимизационных задач – задачи математического программирования, в которых необходимо найти экстремум (максимум или минимум) функции при заданных ограничениях (условиях). Если все функции в модели задачи линейного вида, то имеем задачу линейного программирования(ЗЛП) общего вида:
 (1)
(1)
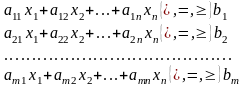 (2)
(2)
(3)
Если все ограничения ЗЛП – неравенства, то запись модели задачи называется стандартной. Если все ограничения ЗЛП –уравнения, то запись модели называется канонической.Правило перехода от стандартной записи модели к канонической мы рассмотрим ниже. Существуют и другие формы записи ЗПЛ (векторная, матричная, с использованием знаков суммирования), с которыми можно познакомиться в учебных изданиях [3], [4].
Примерызадач линейного программирования
1. Задача об оптимальном использовании ресурсов (задача о коврах). В распоряжении фабрики имеется определенное количество ресурсов: рабочая сила (80 чел.-дней), сырье (480 кг), оборудование (130 станко-часов).Фабрика может выпускать ковры четырех типов. Данные о количестве единиц каждого ресурса, необходимых для производства одного ковра каждого типа, и доходах, получаемых предприятием от единицы каждого типа товаров, приведены в таблице:
Ресурсы |
Нормы расхода ресурсов на один ковер |
Наличие ресурсов |
|||
«Лужайка» |
«Силуэт» |
«Детский» |
«Дымка» |
||
Труд |
7 |
2 |
2 |
6 |
80 |
Сырье |
5 |
8 |
4 |
3 |
480 |
Оборудование |
2 |
4 |
1 |
8 |
130 |
Цена ковра, тыс. руб. |
3 |
4 |
3 |
1 |
|
Требуется найти такой план выпуска продукции, при котором общая стоимость продукции будет максимальной.
ЭММ задачи:
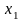 ,
,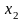 ,
,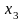 ,
,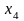 –
искомое оптимальное количество ковров
каждого из четырех типов соответственно;
–
искомое оптимальное количество ковров
каждого из четырех типов соответственно;
F – общая максимальная стоимость продукции (критерий оптимальности);
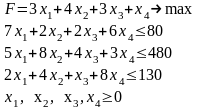
Заметим, что левые части ограничений модели равны фактическим затратам ресурсов при производстве продукции.
2. Задача об инвесторе. Инвестор, располагающий суммой в 300 тыс. ден. ед., может вложить свой капитал в акции автомобильного концерна А и строительного предприятия В. Чтобы уменьшить риск, акций А должно быть приобретено по крайней мере в два раза больше, чем акций В, причем последних можно купить не более чем на 100 тыс. ден. ед.Дивиденды по акциям А составляют 8% в год, по акциям В — 10%. Какую максимальную прибыль можно получить в первый год?
ЭММ задачи:
, – оптимальноеколичество средств, которые необходимо вложить в акцииА и В соответственно;
F – максимальная прибыль инвестора в первый год (критерий оптимальности);
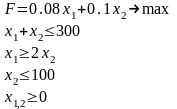
3.
Задача о банке. Пусть
собственные средства банка в сумме с
депозитами составляют Р
млн руб. Часть этих средств, но не менее
Q
млн руб., должна быть размещена в
кредитах, а вложения в ценные бумаги
должны составлять не менее r%
средств, размещенных в кредитах и ценных
бумагах. Если
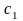 – доходность кредитов,
– доходность кредитов,
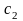 – доходность ценных бумаг (как правило,
>
),
то каково должно быть размещение
средств, чтобы прибыль банка была
максимальной?
– доходность ценных бумаг (как правило,
>
),
то каково должно быть размещение
средств, чтобы прибыль банка была
максимальной?
ЭММ задачи:
, – средства, размещенные в кредитах и вложенные в ценные бумаги соответственно;
F – максимальная прибыль банка;
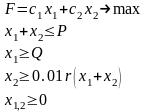
4. Задача о диете (рекомендуется рассмотреть самостоятельно[4]).
Выделяют два основных метода решения задач линейного программирования:
графический,
алгебраический (симплексный).
