2.2. Молекулярная физика и термодинамика
● Количество вещества однородного газа (в молях):
где N – число молекул газа; NA – постоянная Авогадро; m – масса газа; µ – молекулярная масса газа.
Если система представляет смесь нескольких газов, то количество вещества системы:
или
где νi, Ni, mi, μi – соответственно количество вещества, число молекул, масса, молярная масса i – компоненты смеси.
● Уравнение Менделеева – Клапейрона (уравнение состояния идеального газа):
,
где R – универсальная газовая постоянная, Р – давление газа, Т – термодинамическая температура.
● Опытные газовые законы, являющиеся частными случаями уравнения Менделеева – Клапейрона для изопроцессов:
а) закон Бойля-Мариотта (изотермический процесс: Т = const, m = const):
или для двух состояний газа:
б) закон Гей-Люссака (изобарный процесс: Р = const, m = const):
или для двух состояний:
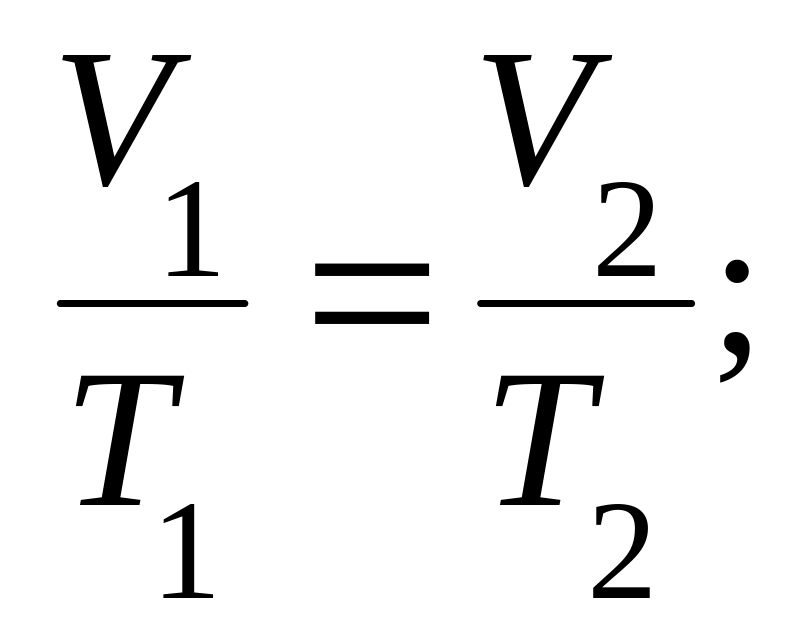
в) закон Шарля (изохорный процесс: V = const, m = const):
или для двух состояний:
г) объединённый газовый закон (m = const):
или
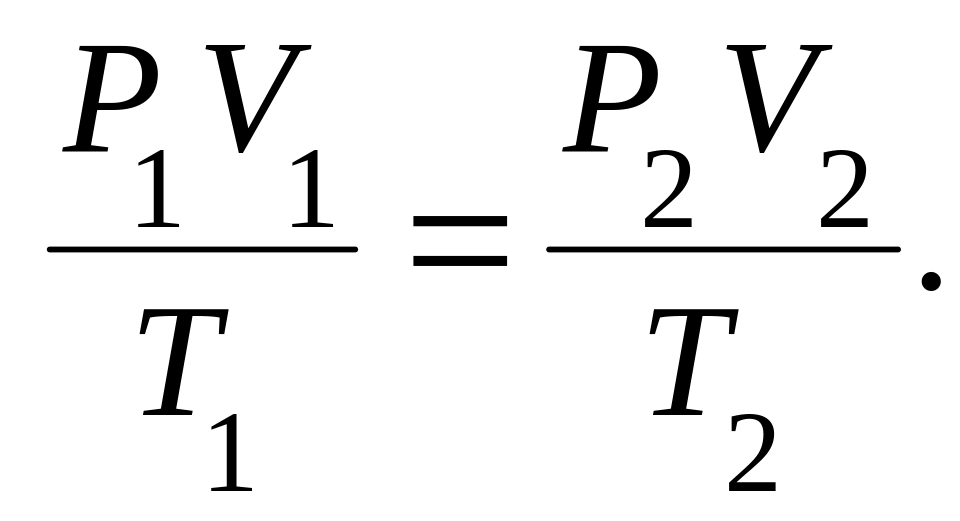
● Закон Дальтона, определяющий давление смеси газов:
где Рi – парциальные давления компонентов смеси; n – число компонентов смеси.
Парциальным называется давление газа, которое производил бы этот газ, если бы только он один находился в сосуде, занятом смесью.
● Молярная масса смеси газов:
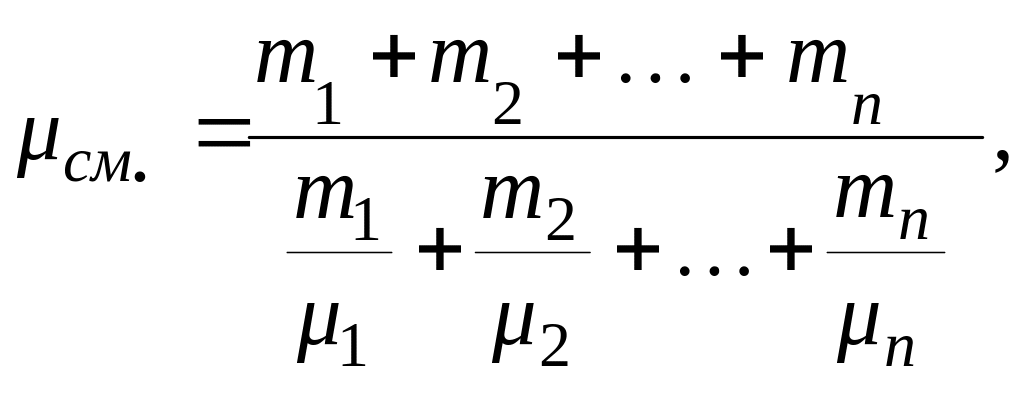
где mi
– масса i-го
компонента смеси;
–
количество вещества i-го
компонента смеси; n
– число компонентов смеси.
● Основное уравнение молекулярно-кинетической теории газов:
где
–
средняя
кинетическая энергия поступательного
движения молекулы.
● Средняя кинетическая энергия поступательного движения молекулы:
где k – постоянная Больцмана.
● Средняя полная кинетическая энергия молекулы:
где i – число степеней свободы молекулы.
● Зависимость давления газа от коцентрации молекул и температуры:
● Скорости молекул:
а) средняя
квадратическая
б) средняя
арифметическая
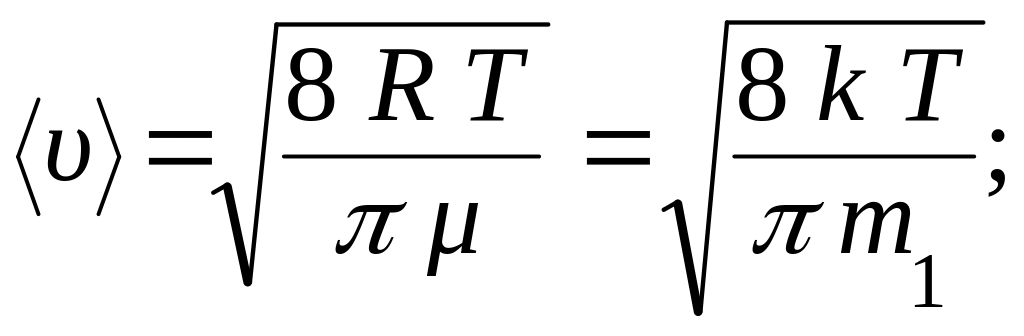
в)
наиболее вероятная
где m1 – масса одной молекулы.
● Средняя длина свободного пробега молекулы:
где d – эффективный диаметр молекулы.
● Среднее число соударений молекулы за 1 секунду:
где n – концентрация молекул.
● Уравнение диффузии (закон Фика):
где dm
– масса газа, которая переносится за
время dt
через элементарную площадку dS
в направлении нормали х
к рассматриваемой площадке в сторону
убывания плотности,
– градиент плотности, D
– коэффициент диффузии.
● Уравнение теплопроводности (закон Фурье):
где dQ
– количество теплоты, переносимое за
время dt
через элементарную площадку dS
в направлении нормали х к этой площадке
в сторону убывания температуры,
– градиент плотности,
– коэффициент теплопроводности.
● Сила внутреннего трения в жидкости и газе (закон Ньютона):
где
– сила внутреннего трения, действующая
на площадку
поверхности слоя,
– градиент скорости движения слоёв в
направлении х,
перпендикулярном к поверхности слоя,
–
коэффициент
внутреннего трения.
● Удельные теплоёмкости газа при постоянном объёме (Сv) и при постоянном давлении (Сp):
и
● Связь между удельной Суд. и молярной Сμ теплоёмкостями:
и
.
● Уравнение Майера:
,
где R – универсальная газовая постоянная.
● Внутренняя энергия идеального газа:
● Первое начало термодинамики:
,
где Q – количество теплоты, сообщённое системе (газу); ∆U – изменение внутренней энергии системы; А – работа, совершаемая системой против внешних сил.
● Работа расширения газа:
а) в общем случае:
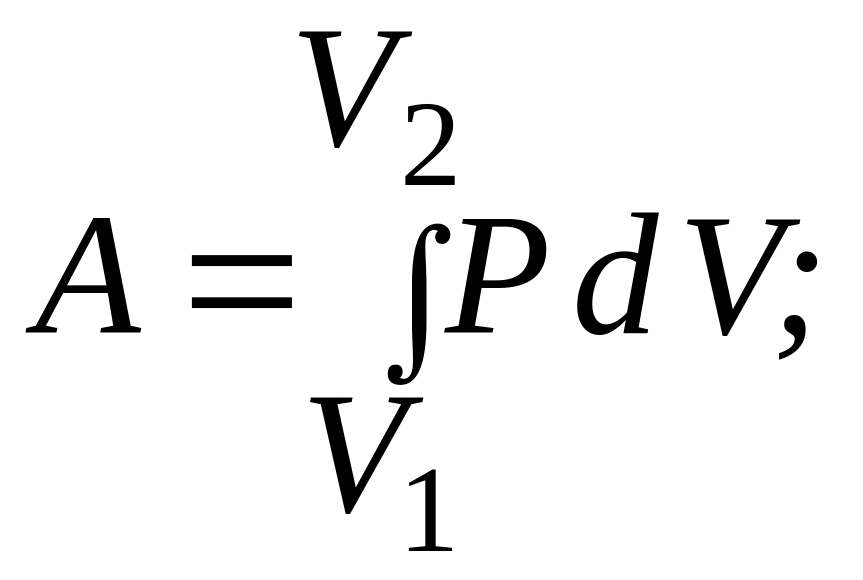
б) при изобарном процессе:
в) при изотермическом процессе:
;
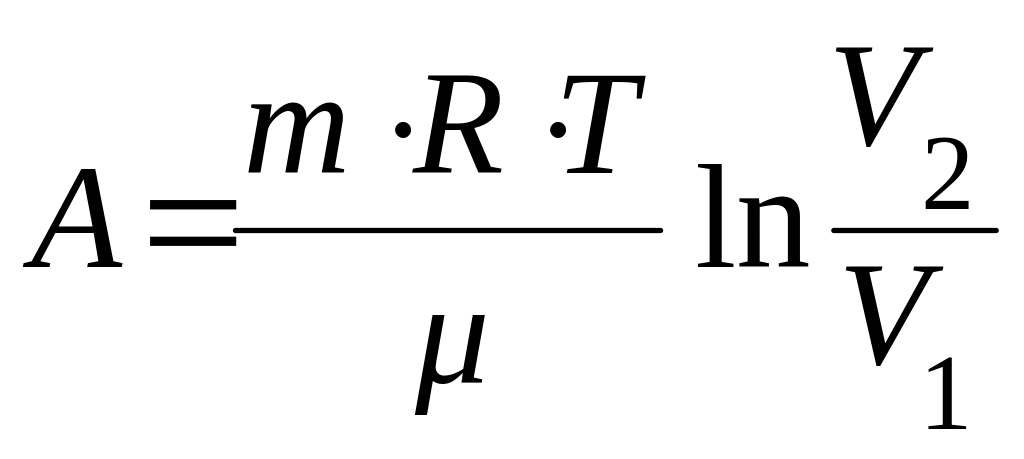г) при адиабатном процессе:
где γ –
–
показатель адиабаты.
● Уравнения Пуассона, связывающее параметры идеального газа при адиабатном процессе:
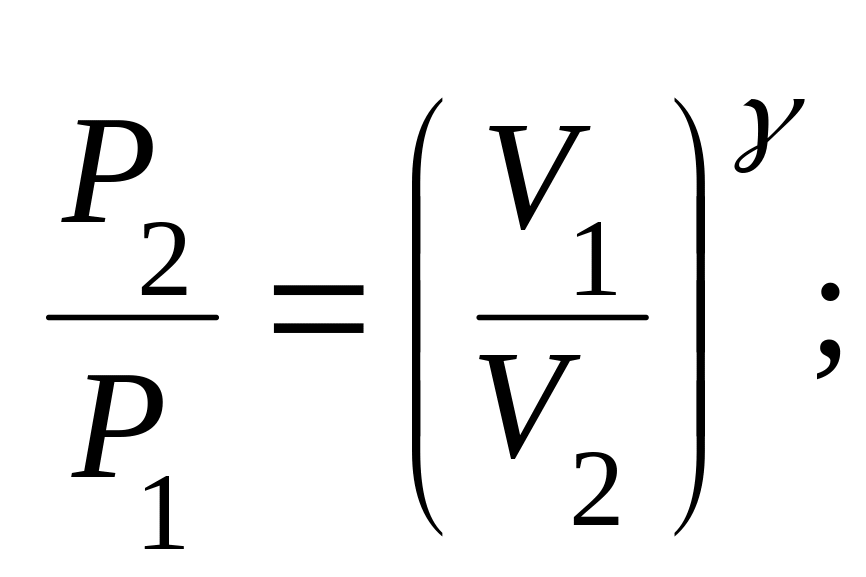
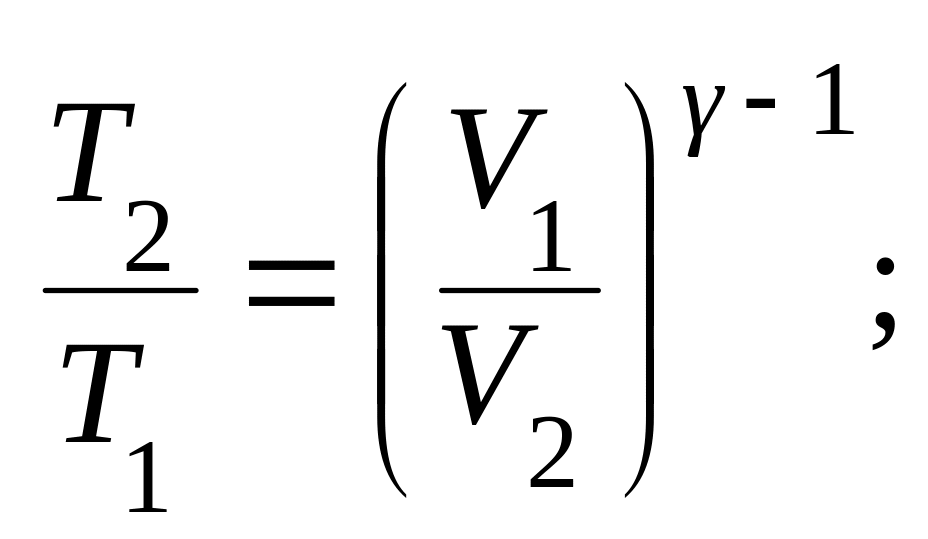
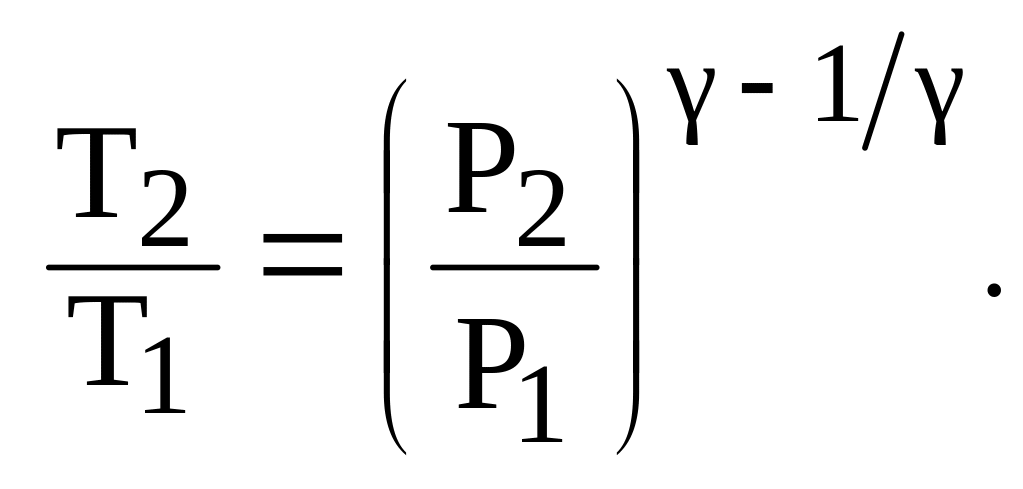
● Термический КПД цикла:
где Q1 – теплота, полученная рабочим телом от теплоотдатчика;
Q2 – теплота, переданная рабочим телом теплоприёмнику.
● Термический коэффициент цикла Карно:
где T1, T2 – термодинамические температуры теплоотдатчика и теплоприёмника.
● Коэффициент поверхностного натяжения:
где F – сила поверхностного натяжения, действующая на контур ℓ, ограничивающий поверхность жидкости;
∆Е – изменение свободной энергии поверхностной плёнки жидкости, связанное с изменением площади ∆S поверхности этой плёнки.
● Формула Лапласа, выражающая давление Р, создаваемое сферической поверхностью жидкости:
где R – радиус сферической поверхности.
● Высота подъёма жидкости в капиллярной трубке:
где
–
краевой угол (
=
0 при полном смачивании стенок трубки
жидкостью,
=
π при полном несмачивании);
R – радиус капилляра; ρ – плотность жидкости; g – ускорение свободного падения.
● Высота подъёма жидкости между двумя близкими и параллельными друг другу плоскостями:
где d – расстояние между плоскостями.