Контрольные вопросы

1. По каким функциям разлагается в ряд Фурье четная (нечетная) функция.

Практическая работа № 3

Тема: «Ряд Фурье с произвольным периодом»

Основные вопросы: Коэффициенты разложения функции с произвольным периодом. Разложение в ряд Фурье функций произвольного периода.

Краткие теоретические сведения: Если функция f(x) в промежутке –l<x<l, где l - произвольное число (l>0), удовлетворяет условиям Дирихле, то ее разложение в ряд Фурье имеет вид

, (5)

где

, , .(6)

Ряд (6) представляет собой функцию с периодом 2l, т. е. f(x+2l)=f(x).

Если f(x) – нечетная функция, то ее ряд Фурье содержит только синусы:

, где . (7)

Если же f(x) – четная функция, то ее ряд Фурье содержит только свободный член и косинусы:

, где , . (8)

Примеры решения задач

Пример 1. Разложить в ряд Фурье функцию, заданную в промежутке уравнением .

Решение. Данная функция является четной. Графиком функции служит дуга параболы, заключенная между точками (-1; 1) и (1; 1).

Рисунок 3

, .

Интегрируем по частям: ; тогда

.

Снова интегрируем по частям: , откуда

.

Подставив это значение в в (5),получим

или .

Пример 2. Разложить в ряд Фурье периодическую (с периодом Т = 2) функцию f(х), заданную на отрезке [-1; 1].

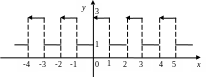
Рисунок 4

Решение. Функция удовлетворяет условиям Дирихле, а поэтому разлагается в ряд Фурье, коэффициенты которого вычислим по известным формулам.

,

,

Ответ: .

Пример 3. Разложить в ряд Фурье периодическую функцию f(х) =│x│, на отрезке [-2; 2].

Рисунок 5

Решение. f(х) =│x│, непрерывная функция, удовлетворяющая условиям теоремы о разложимости, и, следовательно, разлагается в свой ряд Фурье. Она четная, поэтому разлагается в ряд Фурье только по косинусам, т. е. b_n = 0.

Находим коэффициенты а₀ и а_п искомого ряда

,

Ответ: искомый ряд Фурье данной функции

.

Пример 4. Пусть требуется разложить в ряд Фурье периодическую функцию f(х) с периодом Т=2, которая на отрезке [-1; 1] задается равенством f(х) =│x│.

Рисунок 6

Решение. Так как рассматриваемая функция четная l=1, то , _.

Следовательно разложение имеет вид

.

Порядок выполнения работы

1. Разложить в ряд Фурье функцию f(х)=х, заданную в промежутке .

2. Разложить в ряд Фурье периодическую функцию f(х) =│x│, на отрезке .

3. Разложите в ряд Фурье только по синусам функцию , заданную в промежутке .

4. .

5. 

6. 

7. 

8. 

Ответы: 1) .

2)

3) .

4)

5)

6)

7)

8)

Контрольные вопросы

1. Функция разложена в ряд Фурье по синусам на отрезке [0; 1]. Чему равна сумма ряда в точках ? Чему равен период суммы ряда?