1.4.3 Функциональный анализ языка

Множества и кортежи. Рассмотренная типология знаков языка страдает отсутствием четких и единообразных оснований для их классификации. Функциональный анализ позволяет все выражения трактовать либо как знаки функций, либо как знаки их аргументов.

Функциональный анализ языка опирается на ряд основополагающих понятий теории множеств – универсальной общеметодологической теории. Основным является понятие множества (класса), которое представляет собой объект, образованный за счет мысленного собирания в единое целое каких-либо предметов, в том числе и самих множеств. Множества полностью характеризуются теми предметами, которые в них собраны. Чтобы задать множество, достаточно тем или иным способом указать каждый элемент (предмет), содержащийся в нем. Факт вхождения предмета и в множество М выражается записью «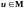 » (отношение принадлежности элемента классу), а факт невхождения – «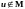 ». В логике множества изображают графически с помощью так называемых кругов Эйлера, а элементы множеств – точками.

Множество может быть задано тремя способами:

1) перечислительно – списком элементов, если число элементов конечно и практически легко обозримо. Списки, задающие множества, заключаются в фигурные скобки, например: {u₁, u₂, u₃};

2) аналитически – посредством некоторого признака, присущего всем его и только его элементам. Например, фраза «множество чисел таких, что они делятся на 2» задает множество четных чисел и записывается так: ;

3) алгоритмически – некоторым конструктивным процессом (алгоритмом), порождающим из одних элементов множества другие его элементы. Например: а) 1 – натуральное число; б) если n есть натуральное число, то n + 1 есть натуральное число; в) ничто, кроме указанного в пунктах а и б, натуральным числом не является.

Множества различаются между собой по мощности, т. е. по количеству входящих в них элементов. По мощности множества делятся на пустые (обозначаются знаком « ») и непустые. Непустые множества бывают конечными и бесконечными. В теории множеств различают сам объект u и одноэлементное множество {u}. Бесконечные множества бывают разной мощности. Наименьшими по мощности являются счетные множества – множества, элементы которого можно поставить во взаимно-однозначное соответствие с натуральными числами, т. е. каждому элементу такого множества можно присвоить свой собственный номер. Все остальные множества являются несчетными.

Множества могут находиться в различных отношениях друг к другу. Если каждый элемент множества M₁ является одновременно и элементом множества M₂, т. е. справедливо утверждение , то говорят, что M₁ является подмножеством M₂. Это отношение называют отношением включения и обозначается так: 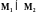. Из данного определения следует: и 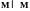. Пустое множество и само множество M называется несобственным подмножеством множества M. Остальные подмножества называются собственными (правильными) подмножествами множества М. Если множества М₁ и М₂ включаются друг в друга, то для них справедливо отношение равенства: или 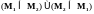. Если множество М₁ (вид) включается в множество М₂ (род), но не наоборот, то говорят о строгом включении: .

Кроме этих трех отношений существуют и другие виды отношений между множествами, а также операции над множествами: сложение, умножение, деление и возведение в степень, а также декартово произведение множеств.

Операцией степени называется операция, которая по произвольному множеству М порождает все его подмножества: . Если М – конечное n-элементное множество, то чтобы образовать множество всех его подмножеств, надо собрать в один класс все нульэлементные, одноэлементные, …, n-элементные подмножества, которые могут быть образованы из элементов множества М.

Кортеж – линейно упорядоченная последовательность предметов. В кортеж один и тот же элемент может входить несколько раз. Для обозначения кортежа используются угловые скобки. Например, < u₁, u₂, u₁, u₁ > обозначает кортеж, представляющий собой четверку элементов. Каждый элемент, входящий в кортеж на определенном месте, называется компонентой.

Кортежи бывают пустыми и непустыми (конечными). Пустой кортеж – это кортеж, не содержащий ни одной компоненты, его длина равна 0 («<>»). Конечные кортежи бывают однокомпонентными, двухкомпонентными и т. д. Для однокомпонентного кортежа выполняется условие: <u> = u.

Два кортежа 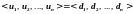, если и только если выполняются следующие условия:

–  , т. е. оба кортежа имеют одинаковое количество компонент (одинаковую длину);

–  , т. е. какие бы i-е компоненты обоих кортежей мы не взяли, должно быть верно, что эти компоненты обоих кортежей представляют собой один и тот же элемент – .

Все выражения естественных языков представляют собой конечные линейно упорядоченные последовательности букв алфавита, поэтому к ним применимо все, что говорится о кортежах. Равенство указанного типа называется графическим равенством и будет обозначаться знаком « ».

Декартовым произведением двух множеств М₁ и М₂ (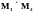 ) называется множество всех возможных пар < x, y > таких, что x является элементом первого множества, а y – элементом второго множества, т. е.

.

Порядок перемножения множеств значим. Аналогично можно ввести операцию декартова произведения трех, четырех и вообще n множеств.

Декартовым произведением n множеств является множество 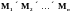всех упорядоченных n-значений таких, что x₁ – элемент первого множества, x₂ – элемент второго множества,…, x_n – элемент n-го множества, т. е.

.

Когда некоторое множество М перемножается n раз само на себя, декартово произведение обозначается выражением Mⁿ и называется n-й декартовой степенью множества М.

Теоретико-множественная трактовка свойств и отношений. Термины «свойства» и «отношения» при их экстенсиональном понимании трактуются как некоторые множества.

Свойством R, заданном на множестве М, называется любое подмножество множества М, т. е. .

Отношением R, заданным на множествах 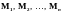, является любое подмножество декартова произведения , т. е. .

Если некоторый кортеж длины декартова произведения является элементом подмножества R, что записывается как , то говорят о том, что переменные 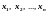находятся в отношении R, что записывается так: 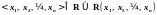. В случае, когда R является подмножеством декартовой степени Mⁿ, т. е. , говорят, что R задано на множестве М. Если 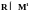, где М¹ – первая декартова степень множества М, то в силу соответствия <u> = u, т. е. 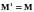. В этом случае R является свойством, заданным на множестве М.

Если хотя бы одно из множеств 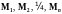заменяется другим множеством, мы имеем дело с другим отношением. При употреблении предикатора, выражающего отношение, необходимо каждый раз уточнять, на каких конкретно множествах оно задано. Для любых двух n-местных отношений R₁ и R₂ (n = 1, 2, …) справедливо:

.

Свойства двухместных отношений. Пусть R будет двухместным отношением, заданным на множестве A, а индивидные переменные x, y и z пробегают по этому множеству. Будем тогда говорить, что:

– R рефлексивно, е. т. е. ;

– R антирефлексивно, е. т. е. ;

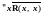– R нерефлексивно, е. т. е. ;

– R симметрично, е. т. е. ;

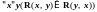– R несимметрично, е. т. е. ;

– R асимметрично, е. т. е. ;

– R антисимметрично, е. т. е. ;

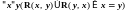– R транзитивно, е. т. е. .

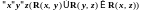На основе этих отношений можно ввести отношения равенства и порядка. R – отношение равенства, если и только если R обладает свойствами рефлексивности, симметричности и транзитивности. R – отношение порядка, если и только если R антирефлексивно, асимметрично и транзитивно. Множество, на котором задано отношение порядка, называется упорядоченным множеством.

Элемент x множества М называют наименьшим, если для любого y  М, не совпадающего с x, верно, что x < y.

Порядок на множестве М, заданном отношением R, называется линейным, если любые два несовпадающие элемента М сравнимы, т. е. для них верна запись: 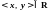или . Про множество в этом случае говорят, что оно линейно упорядочено или является цепью.

Упорядоченное множество М называется деревом, если: 1) из того, что y < x и z < x, следует, что y и z сравнимы; 2) в множестве М существует наименьший элемент, называемый корнем дерева.

Функции. Для логики большое значение имеет понятие функции, которое позволяет уточнить смысл ряда семантических категорий: n + 1-местное отношение , заданное на декартовом произведении , называется функциональным отношением, если и только если для каждого упорядоченного множества объектов существует ровно один предмет такой, что .

Более распространенным является нестрогое определение функции: n-местная функция f есть отображение, которое каждому элементу множества 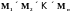ставит в соответствие ровно один элемент множества М.

При этом декартово произведение 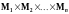называется областью определения n-местной функции f, а множество М – областью ее значений. Каждое М_i является областью возможных значений переменной x_i. Элементы x₁, x₂, …, x_n называются аргументами функции f; а y – значением функции при данном наборе аргументов и обозначается выражением вида . Таким образом, можно вывести зависимость:

.

Таким образом, функция – это всюду определенное и однозначное отображение. Информацию о наличии отображения элементов множества в множество М принято записывать в виде .

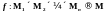В случае отображения множества Mⁿ в множество М, т. е. когда возможные области изменения каждого из аргументов совпадают между собой, а также с областью значений, эта информация записывается в форме . Тогда говорят, что функция f является операцией, заданной на множестве М.

Элементы области определения функции в зависимости от ее местности могут быть либо отдельно взятыми объектами или же кортежами разной длины. Местность функции определяется длиной кортежей, которые входят в область определения соответствующей функции. Неопределенноместная функция – это функция, область определения которой в разных случаях состоит из кортежей разной длины. Функции f₁ и f₂ являются равными друг другу, если у них совпадают области определения и значения, а также на одинаковых наборах аргументов они принимают одинаковые значения.

Из всего вышесказанного следует, что задать некоторую функцию – значит: 1) задать область определения функции, 2) задать область ее значения и 3) указать, какие элементы из области определения и области значения связываются этой функцией.

Функция может быть задана графически, таблично, аналитически. Наиболее распространенным является последний способ. В последнем случае формулируется некоторое правило, согласно которому элементам области определения функции сопоставляются элементы области значения функции. Это правило выражается в языке конструкцией вида 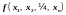, состоящей из знака функции (функтора) и переменных, причем с каждой переменной 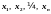связано свое множество (область пробега соответствующей переменной), а сами элементы этих множеств называются возможными значениями аргументов функции. Данная конструкция называется аналитическим представлением функции.

При аналитическом задании функции с помощью выражений важным оказывается различение фиктивного и существенного вхождения переменных в это значение. Переменная входит в выражение фиктивно, если любое изменение ее значений, которые она может принять в множестве М_i, не влияет на изменения значения всего выражения. В противном случае переменная x_i входит в выражение существенно. Зачастую аналитический способ предполагает формулирование некоторого правила, согласно которому элементам области определения функции сопоставляются элементы области значения функции.

Функции можно подразделить на виды в зависимости от того, какого типа объекты являются их возможными аргументами и возможными значениями. С точки зрения логики, значимым представляется подразделение объектов на индивиды и истинностные оценки. С учетом этого можно выделить предметно-предметные, (аргументы и значения – индивиды), предметно-истинностные (аргументами являются предметы, а значениями – истинностные оценки) и истинно-истинностные (аргументы и значения – истинностные оценки) функции. Последние два вида функций называют логическими.

Если проанализировать с точки зрения функционального подхода семантические категории естественного языка, то можно констатировать факт, что предметными функторы, предикаторы и логические константы – знаки функций.

Предметные функторы – это знаки предметно-предметных функций различной местности, а имена – это знаки нульместных предметно-предметных функций. Предметно-предметные функции выражаются посредством именных форм, т. е. такими выражениями, в результате подстановки в которые вместо предметных знаков имен получается новое имя.

Предикаторы – знаки предметно-истинностных функций различной местности, а предложения – нульместных истинностных функций. Предметно-истинностные функции выражаются высказывательными формами.

Пропозициональные связки – это знаки истинностно-истинностных функций различной местности. В классической логике к истинностно-истинностным функциям относят все функции вида . Функции этого вида называются булевыми функциями. К ним относятся конъюнкция ( – соединительная связка «и»), дизъюнкция ( – разделительная связка «или»), импликация ( – условная связка «если ..., то ...»), эквиваленция ( – связка «если и только если ..., то ...») и отрицание ( – унарная связка «неверно, что ...»). Однако необходимо помнить, что истинностно-функциональными являются далеко не все пропозициональные связки. Перечисленные связки трактуются в логике экстенсионально. Последовательная конъюнкция, релевантная импликация, модальные операторы (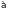 – возможно, – случайно, – необходимо) и другие связки не относятся к числу истинностно-функциональных знаков.