21. Изобразить прямой цикл Карно в pv и ts-диаграммах, составить ф-лу термического кпд цикла Карно.
Среди всех возможных прямых циклов имеет самый высокий термический КПД.
Этот цикл был предложен в 1824 г. французским инженером и ученым Сади Карно. Цикл Карно состоит из конкретных процессов: двух изотерм и двух адиабат (рис. 1.11).
Здесь 1 кг газа расширяется в цилиндре по изотерме 1–2 с подводом теплоты q1, затем по адиабате 2–3, совершая значительную работу (площадь 1233’1’1). Затем газ сжимается по изотерме 3–4 с отводом теплоты q2 и адиабате 4–1, на что затрачивается работа (площадь 3411’3’3).Из точки 1 цикл повторяется.
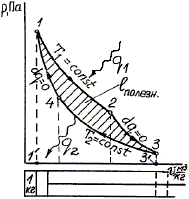
На рис. 1.16 1 кг газа расширяется по изотерме 1–2 с подводом теплоты q1, равной площади 122’1’1, а затем по адиабате 2–3. В исходное состояние газ возвращается сжатием по изотерме 3–4 с отводом теплоты q2, равной площади 341’2’3, затем – по адиабате 4–1. Теплота, превратившаяся в полезную работу, qп = q1–q2 = площадь 122’1’1 – площадь 341’2’3 = площади 12341, т.е. равна площади внутри цикла.Pис. 1.16 Прямой цикл Карно в TS координатах
Найдем термический КПД цикла Карно для PV диаграммы, учитывая равенство работы и теплоты в изотермическом процессе:
для PV
где T1, T2 – соответственно температуры теплового источника и теплового приемника (наибольшая и наименьшая температуры в цикле).
Рассмотрев
совместно процессы, составляющие цикл
Карно, нетрудно показать, что
, и КПД определится по формуле
(1.24)
Найдем термический КПД цикла Карно для PV диаграммы,
для TS.
(1.29)
Цикл Карно называют идеальным, так как он лучше других циклов превращает теплоту q1 в полезную работу. С другой стороны, из-за трудности в организации изотермических процессов он не применяется в реальном двигателе.
22. Записать основные свойства цикла Карно и его значение в термодинамике.
|
Рисунок 3.11.1. Круговой процесс на диаграмме (p, V). abc – кривая расширения, cda – кривая сжатия. Работа Aв круговом процессе равна площади фигуры abcd |
Термодинами́ческие ци́клы — круговые процессы в термодинамике, то есть такие процессы, в которых совпадают начальные и конечные параметры, определяющие состояние рабочего тела: (давление, объём,температура и энтропия).
Прямой цикл - циклический процесс, в котором расширение рабочего тела осуществляется при более высокой температуре, чем сжатие.
Цикл Карно - идеальный обратимый термодинамический цикл, образованный двумя изотермическими и двумя адиабатическими процессами. Цикл Карно соответствует максимальному превращению тепла в механическую энергию.
Общее свойство всех круговых процессов состоит в том, что их невозможно провести, приводя рабочее тело в тепловой контакт только с одним тепловым резервуаром. Их нужно, по крайней мере, два. Тепловой резервуар с более высокой температурой называют нагревателем, а с более низкой – холодильником. Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты Q1 > 0 и отдает холодильнику количество теплоты Q2 < 0. Полное количество теплоты Q, полученное рабочим телом за цикл, равно
Q = Q1 + Q2 = Q1 – |Q2|. |