Корреляционное отношение

Мерой тесноты нелинейной связи является корреляционное отношение.

Рассмотрим корреляционную зависимость . Разобьем диапазон изменения x на R интервалов, в каждом интервале найдём условные средние и условную дисперсию.

Найдем общую среднюю и общую дисперсию:

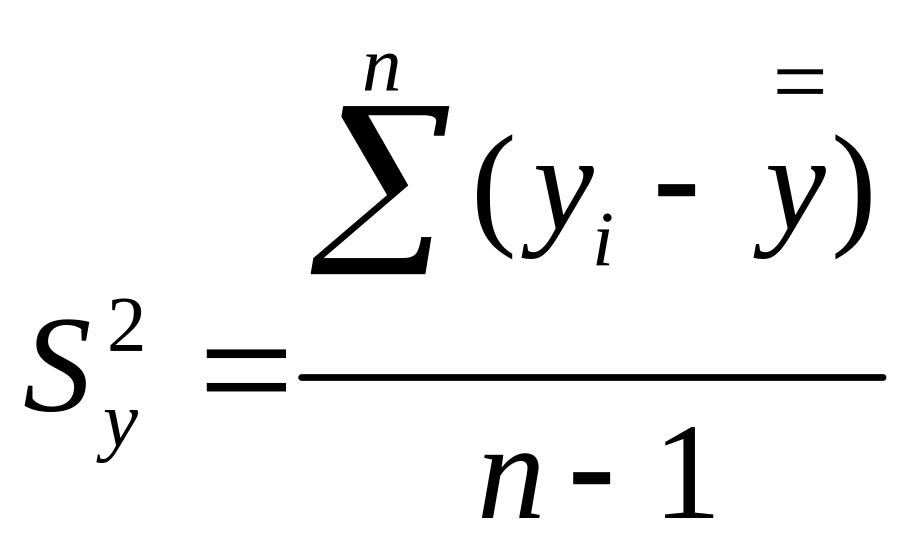
Найдем среднеквадратичное отклонение условных средних от общего среднего:

Если - одинакова, то

Тогда или

- это корреляционное отношение.

Если , то между величинами существует нелинейная функциональная связь.

Если , то связь отсутствует, т.е величины независимы.

		Характер связи
	-	Линейная функциональная
0	1	Криволинейная функциональная
0	0	Отсутствует
0	<1	Криволинейная корреляционная
	<1	Линейная корреляционная

Проверка адекватности модели.

Р ассмотрим две серии испытании, в которых средние значения одинаковы, а разбросы разные. Аппроксимируем экспериментальные значения прямой.

В первом случае прямая не выходит за пределы доверительных границ, следовательно, она может быть теоретической линией регрессии. Значит прямая адекватно описывает процесс.

Во втором случае прямая выходит за пределы доверительных границ, значит она не может быть линией регрессии. Значит прямая неадекватно описывает процесс.

Для проверки адекватности используют критерии Фишера.

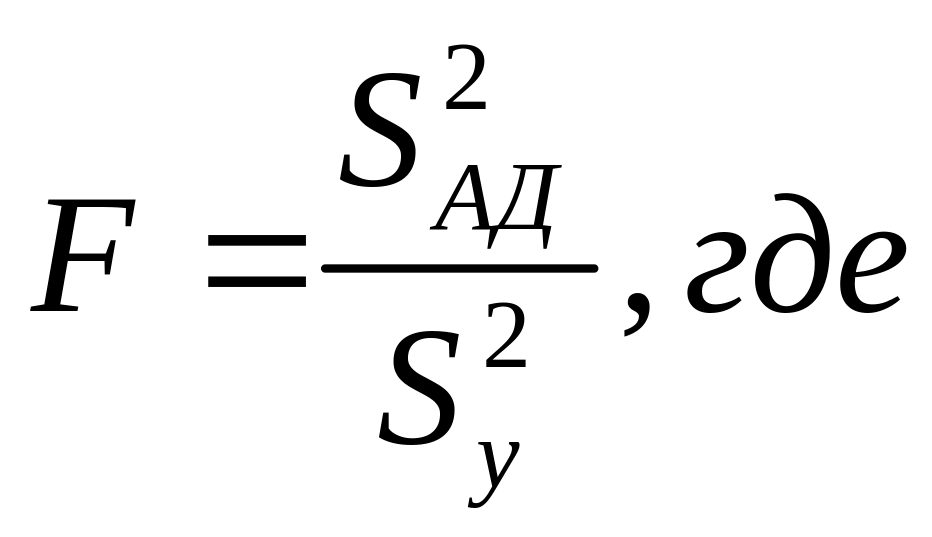
- дисперсия адекватности.

- дисперсия воспроизводимости.

Если , то модель адекватна.

Дисперсия воспроизводимости характеризует разброс экспериментальных точек относительно их средних значении и определяется как средневзвешенное по всем опытам.

- количество точек (опытов),

- количество повторении в точках.

Число степеней свободы

Дисперсия адекватности характеризует отклонение средних значении от линии регрессии.

Число степеней свободы равно разности между числом опытов, результаты которых используются при расчете коэффициентов уравнения регрессии и числом определяемых коэффициентов.

Сравнение двух испытаний.

Цель сравнения – установить, является ли различия случайными или существенными (значимыми).

1. Сравнение средних при известной дисперсии производится по критерию нормального распределения:

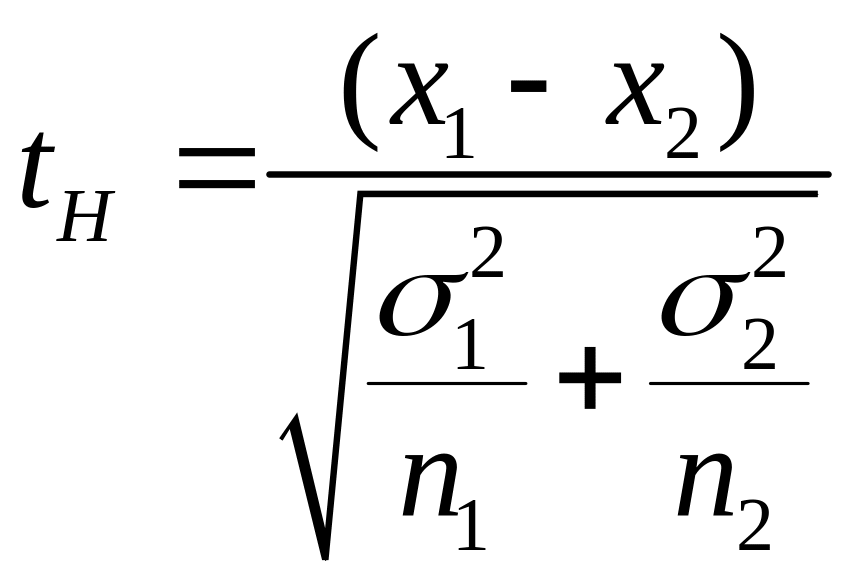
Если , то различия значимы, где t- квантиль нормального распределения.

2. Сравнение средних при неизвестной дисперсии производится по критерию Стьюдента:

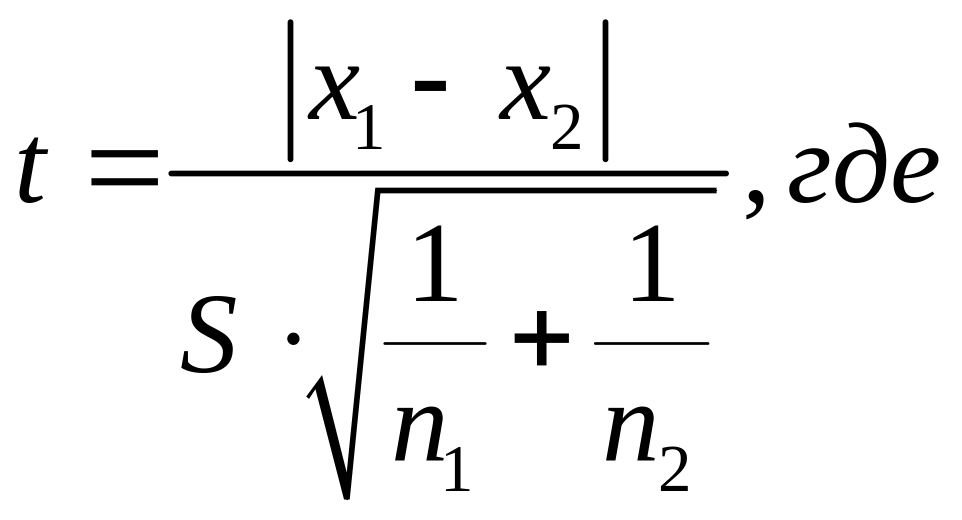
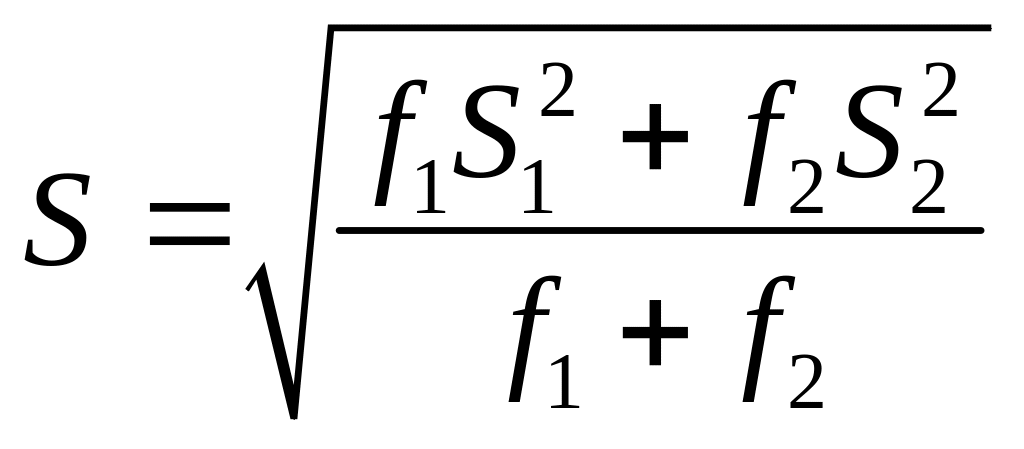- средневзвешенная дисперсия.

- число степеней свободы.

Если , то различие значимо.

3. Определение грубых ошибок (выскакивающие значения :

Если , то отбрасывают.

4. Сравнение двух дисперсии производится по критерию Фишера:

- большая дисперсия.

Если , то различие не случайно,

Если , то выборка имеет одинаковую генеральную дисперсию Случайные функции

С лучайной называется функцию, которая для каждого заданного значения аргумента является случайной величиной. Полученный в результате опыта конкретный вид случайной функции называется реализацией или выборочной функцией.

Рассеивание размеров в каждый данный момент времени называется мгновенным рассеиванием. Исчерпывающей характеристикой случайной функции являются последовательностью плотностей вероятности (мгновенных плотностей).

Для решения практических задач достаточно знать: математическое ожидание, дисперсию, корреляционную функцию или спектр.

Математическим ожиданием (дисперсией) случайной функции x(t) называется неслучайная функция , которая при каждом данном значении аргумента t равна математическому ожиданию (дисперсии) случайной функции. При этом t:

Корреляционная или автокорреляционная функция равна коэффициенту корреляции между и .

Случайную функцию можно представить в виде ряда Фурье:

(1)

Где коэффициенты Фурье:

(2)

(3)

Где T- период времени (длина участка) измерения.

К- номер гармоники.

Гармоническую часть можно переписать в виде:

(4)

Где - амплитуда (случайная) (5)

- случайная фаза

Если вероятностные характеристики не зависят от t, то функция называется стационарной. У стационарной функции дисперсия постоянна, а автокорреляционная функция зависит только от , причем ( ).