1.2. Задачи на движение

При решении задач на составление уравнений наиболь­шую трудность обычно вызывает составление уравнений или системы уравнений, а уж потом их решение. И в том и в другом случае часто оказывается полезным рисунок, иллюстрирующий условие задачи и его анализ с точки зрения геометрии. Вводят координатную плоскость, по одной из осей которой от­кладывается время, по другой — путь, пройденный телом, выполненная работа и т. д. Тогда любая точ­ка этой плоскости с координатами (t, s) будет соответ­ствовать, например, пути S, пройденному объектом за время t, а само движение изобразится некоторой линией в этой плоскости (траекторией).

Пример 4. Из пункта М в пункт N вышел пешеход. Вслед за ним через 2 ч из пункта М выехал велосипедист, а еще через 30 мин — мотоциклист. Пеше­ход, велосипедист и мотоциклист двигались равномерно и без остановок. Через некоторое время оказалось, что все трое преодолели одинаковую часть пути от М к N. На сколько минут раньше пешехода в пункт N прибыл вело­сипедист, если пешеход прибыл в пункт N на 1 ч позже мото­циклиста?

Решение.

Рассмотрим плоскость, по оси абсцисс которой отложим время, а по оси ординат — пройденный путь (рис. 5). Пусть отрезок ОЕ соответствует пути, пройденному пеше­ходом, отрезок AD — велосипедистом, прямая ВС — мото­циклистом. Так как в некоторый момент времени они на­ходятся в одной точке, то все три отрезка имеют на рисунке общую точку.

Рис. 5

В соответствии с условием задачи OA=2, AB=0,5, СЕ=1; требуется найти DE. Так как прямые СЕ и ОВ параллельны, то OB/CE=OA/DE или DE=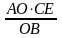 , откуда x=4/5 ч или 48 мин.

Ответ: 48 мин.

Пример 5. Из пункта А в пункт В вышел пешеход. Одновременно с ним из пункта В в пункт А выехал велосипедист, который встретил пешехода через 50 мин после своего выезда из В. Сколько времени потре­бовалось бы пешеходу для того, чтобы пройти весь путь из А в В, если известно, что велосипедист проделал бы тот же путь на 4 ч быстрее пешехода (рис. 6.6).

Решение.

Пусть BD — траектория велосипедиста, АС — траектория пешехода, t — время, затраченное пешеходом на путь от А до В (в ч).

Рис. 6

Имеем: СОО" ~ ОО'А, откуда СО"/О'А = = 00"/00', D00'~ 00"B, откуда O"B/O'D=00"/00', следовательно,

, или .

Это уравнение сводится к квадратному относительно t, решая которое получим t₁ = 2/3, t₂ = 5.

Ответ: t = 5 ч.

Пример 6. Из пункта А в пункт В отправились одновре­менно пешеход и велосипедист. Велосипедист, доехав до пункта В, повернул обратно и встретил пешехода через 20 мин после отправления из А. Доехав до А, он опять по­вернул и догнал пешехода через 10 мин после встречи. Через какое время пешеход придет в В?

Решение.

Линия AB'DK (рис.7) соответствует пути, который проехал велосипедист, АК — пути, пройденному пешеходом, АС'=20, С'К'=10, CDK~ CB'A, откуда

.

Рис. 7

Следовательно, AN= АВ. Таким образом, на 1/3 пути (АС) пешеход затратил 20 мин, а на весь путь он за­тратит 1 ч.

Ответ: 1 ч.

1.3. Задачи на совместную работу

Решению таких задач, как правило, предшествует графическая интерпретация условия. Традиционные подходы не всегда позволяют сделать чертёж наглядным, дающим полноценное представление о действиях, описанных в задаче. Если речь идёт о равномерной работе, то рассматриваемые процессы удобно иллюстрировать графиками функций выполненной работы от времени. Такой подход позволяет давать графикам геометрическую интерпретацию. На смену составлению и решению сложных систем уравнений приходит использование геометрических свойств фигур: подобия треугольников, свойства пропорциональных отрезков и т. д.

Пример 7. Баржа была разгружена с помощью двух кранов на протяжении 15ч, причём первый крановщик приступил к работе на 7 ч позже второго. Известно, что первый крановщик, работая отдельно, может разгрузить баржу на 5 ч быстрее второго. За сколько времени может разгрузить баржу каждый крановщик, работая отдельно?

Решение.

Пусть FC=x ч – неизвестный промежуток времени (рис. 8).

Рис. 8

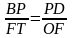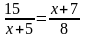; , откуда x = 5.

Тогда AT = 15 + 5 + 5 = 25 ч, OM = 25 – 5 = 20 ч.

Ответ: 25 ч, 20 ч.

Пример 8. Две машинистки должны отпечатать рукописи с одинаковым числом страниц. Первая приступила к работе на 3 ч раньше второй и отпечатала к определённому моменту времени больше, чем вторая, на страниц рукописи. Проработав после этого момента ещё 5 ч, обе машинистки одновременно закончи­ли каждая свою работу. За сколько времени каждая отпечатала свою рукопись?

Решение.

Пусть весь объём работы равен 1, BС = х ч — промежуток времени, недостающий для нахождения времени работы каждой машинистки (рис. 9).

Рис. 9

BED ~ BMC, , т.е. , следовательно, .

OED ~ OKC, следовательно, , т.е. , x = 1 ч, значит первая машинистка работала 8+1=9 ч, вторая машинистка – 1 + 5 = 6ч.

Ответ: 9ч; 6ч.

Пример 9. Двое рабочих могут выпол­нить некоторую работу за 12 дней. После 8 дней совместной работы второй рабочий перешёл на другой участок. Первый рабо­чий закончил работу за 5 дней. За сколь­ко дней каждый рабочий, работая отдель­но, может выполнить данную работу?

Решение.

Обозначим через х дней и у дней неизвестные промежутки времени (рис. 6.10).

; , откуда .

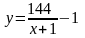Так как BO₂T ~ CO₂N и DO₁P ~ AO₁F, то ;

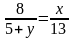, откуда .

Рис. 10

Таким образом, , откуда x = 2 ( x > 0), y = 47.

Тогда BD = 13 + 2 = 15 дней, AC = 13 + 47 = 60 дней.

Ответ: 15 дней, 60 дней.