1. Числовые неравенства. Свойства числовых неравенств.

Для любых неравных действительных чисел a и b можно сказать, какое из них больше, а какое меньше.

Говорят, что число a больше числа b , и пишут a>b, если разность a-b --положительное число; если же разность a-b – отрицательное число, то говорят, что число a меньше числа b и пишут a<b.

Для любых данных действительных чисел a и b имеет место одно из отношений: a=b, a<b, a>b.

Верность некоторых числовых неравенств не всегда очевидна. Например, имеет ли место неравенство не очевидно. В таких случаях неравенства нужно доказывать. При этом важную роль играют утверждения, которые непосредственно следуют из определений сравнения действительных чисел и действия вычитания:

1. Два действительных числа a и b равны тогда и только тогда, когда их разность равна 0, т.е. a-b=0.

2. Число a больше числа b (a>b) тогда и только тогда, когда разность a-b положительна, т.е. a-b>0.

3. Число a меньше числа b (a<b) тогда и только тогда, когда разность a-b отрицательна, т. е. a-b<0.

Перечислим свойства числовых неравенств, которые принято считать основными в школьном курсе математики:

1. Если a>b, то b<a.

2. Если a>b и b>c, то a>c ( свойство транзитивности).

3. Если a>b, то a=b+h, где h>0, и наоборот, если a=b+h ,где h>0, то a>b.

4. Если a>b и c – действительное число, то a+c>b+c.

5. Если a>b и c>d , то a+c>b+d.

6. Если a>b и c>0, то ac>bc.

7. Если a>b и c<0, то ac<bc.

8. Если a>b>0 и c>d>0, то ac>bd

Аналогично можно сформулировать свойства для отношений «меньше», «меньше или равно», «больше или равно».

Перечисленные свойства числовых неравенств легко доказать с помощью определения.

2. Методы доказательства неравенств.

Доказать неравенство – это значит установить его справедливость для всех возможных или специально указанных значений переменных. Универсального метода доказательства неравенств нет. Рассмотрим наиболее часто встречающиеся методы.

1. Метод оценки знака разности левой и правой частей неравенства.

Суть метода заключается в следующем: для того, чтобы установить истинность неравенства F(x,y,…,t)>P(x,y,…,t) (F<P, ) на заданном множестве значений переменных x,y,…t составляют разность

F(x,y,…t)-P(x,y,…t) и доказывают, что она положительна (соответственно, отрицательна, неположительна, неотрицательна) для всех указанных значений x,y,…t.

П р и м е р. Доказать неравенство , если .

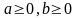Доказательство. Составим разность между частями неравенства и докажем, что она неотрицательна.

т.к. и для всех .

Таким образом, для

2. Доказательство неравенств на основании опорных неравенств.

Суть этого метода заключается в следующем: с помощью ряда преобразований выводят требуемое неравенство из некоторых известных (опорных) неравенств. В качестве опорных могут использоваться, например, следующие неравенства:

1)

2) (неравенство Коши).

3) .

4) и и т.д.

П р и м е р. Доказать неравенство .

Доказательство. В качестве опорного возьмём неравенство Коши.

; ; .

Складываем почленно эти три неравенства и получаем: .

П р и м е р. Доказать, что если то .

Доказательство. Возьмём в качестве опорных следующие неравенства:

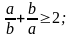
Сложив их, получим , или

Далее выполним ряд несложных преобразований:

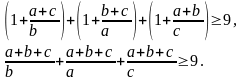
Вынося теперь за скобки, получим:

Знак равенства имеет место лишь в том случае, когда