2. Теоретическое обоснование методов функционального подхода.

К сожалению, изучению функционального и графического метода (свойства функций, заданных в постановке задачи, решения уравнений, неравенств и систем) в программе общеобразовательной школы уделяется незаслуженно мало внимания. Функциональный метод решения задач во многих случаях является более удобным и кратким, нежели алгебраический. И хотя в экзаменационных заданиях крайне редко требуется графическое представление решения, умение строить графики функций, уравнений и изображать на координатной плоскости подмножества может оказаться чрезвычайно полезным, особенно при выполнении тестов, когда время ограничено и значение имеет не способ решения, а только ответ.

Например, умение строить графики функций, уравнений, изображать на координатной плоскости множества решений неравенств часто позволяет избежать громоздких решений многих сложных систем, уравнений и неравенств, например содержащих модули. Такой подход значительно ускоряет нахождение ответа. Незаменимыми оказываются эти методы и при решении задач с параметрами.

Незаменимы построения на координатной плоскости хОу и при решении задач с параметрами. Например, если стоит задача указать количество решений уравнения

f(x)=g(a) (1)

в зависимости от значения параметра а и легко построить график функции

у = g(х) ‚то, учитывая, что у = g (а) — это семейство прямых параллельных оси Ох, а с геометрической точки зрения решения уравнения (1) при фиксированном значении а₀ - это абсциссы точек пересечения графиков, обычно легко записать ответ. Аналогичный подход можно реализовать и в более сложных случаях, а также и при решении так называемых (нестандартных задач).

Основные теоремы, необходимые для решения уравнений, основанных на ограниченности функций

Основная идея метода мажорант состоит в использовании следующих утверждений.

Теорема 1. Если для всех х  Х справедливы неравенства f(х) > А и g(х) <А, где А - некоторое число, то на множестве Х уравнение f (х) = g (х) и неравенство f(х) < g(х) решений не имеют, а неравенство f(х)>g(х) выполняется для всех х  Х

Теорема 2. Если для всех х Х справедливы неравенства f (х) ≥А и g(х)≤А , где А - некоторое число, то на множестве Х уравнение f (х) = g (х) и неравенство f (х) ≤g (х) равносильны системе уравнений

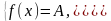
а неравенство f (х) ≥ g (х) выполняется для всех х Î Х.

Отметим, что в качестве множества Х часто принимается общая область определения функций у = f (х) и у = g (х).

Основные теоремы, необходимые для решения уравнений, основанных на ограниченности функций

Теорема 1.Если f (х) — возрастающая на множестве М функция, g (х) - убывающая на множестве М функция и уравнение f(х) = g(х) имеет на множестве М решение х₀, то это решение - единственное на множестве М.

Доказательство.

Так как х₀ - корень, то f(х₀)=g(х₀). Если х<х₀, то f(х)<f(х₀) поскольку f (х) - возрастающая функция, а g(х)> g(х₀) в силу того, что она является убывающей. Значит, f(х) < g(х), и на множестве х<х₀ уравнение f (х)= g (х) не имеет решений. Если х>х₀, то f(х)>f(х₀), а g(х)< g(х₀), поскольку f, g - монотонные функции. Следовательно, f(х)>g(х) и уравнение f(х)=g(х) не имеет решений на множестве х> х₀. Итак, х₀ - единственный корень.

Следствие. Если f(х) - возрастающая на множестве М функция, g (х) - убывающая и уравнение f(х)=g(х) имеет на множестве М решение х₀, то решением неравенства f(х) > g (х) являются все хÎМ такие, что х>х₀, а решением неравенства f (х)< g(x) - все х Î М такие, что х< х₀.

Теорема 2. Если f (х) - возрастающая (убывающая) на множестве М функция, то уравнение f(х)=С, где С - некоторое действительное число, имеет не более одного решения на множестве М.

Теорема 3. Если f(х) - возрастающая (убывающая), непрерывная функция на отрезке [a, b], то f (х) принимает все значения между f (а) и f (b), причем каждое из них лишь при одном x Î [a;b].

Следствие. Если f(х) возрастающая (убывающая), непрерывная функция на отрезке [a;b] и f(a)f(b)<0, то существует, причем единственное, решение уравнения f (х)=0 на (а;b).

Теорема 4. Если f(х) - возрастающая (убывающая) функция, определенная на всей числовой прямой, то уравнения f(g(х)) = f(h(х)) и g(х)=h(х) - равносильны.

Монотонность в условии теоремы 4 нужна, чтобы не происходило потери корней при переходе к уравнению g(х)= h(х). А функция f должна быть определена на всей числовой прямой, чтобы не было приобретения корней при переходе к уравнению g(х)= h(х).

Даже если f(х) определена не при всех х ÎR, то посторонние корни, которые могут появиться при переходе к уравнению-следствию g(х)= h(х), затем обычно легко отсеять проверкой.

Замечание 1. Если f (х) - возрастающая (убывающая) функция на ОДЗ переменной уравнения f(g(х))= f(h(х)), то последнее уравнение равносильно уравнению g(х)= h(х) на множестве допустимых значений переменной х.

Замечание 2. Если f (х) является четной и возрастает (убывает) при х≥0, то f(g(х))= f(h(х))  на ОДЗ переменной х.

Теорема 5. Если f (х) - возрастающая на множестве М функция и при любом х Î М значение функции принадлежит М, то уравнения f(f(х))=х и f(х)=х равносильны.