2.2.3 Куча Фибоначчи

Фибоначчиева куча — набор деревьев Фибоначчи, корни которых объединены в неупорядоченный циклический двусвязный список. В отличие от биномиальной кучи, степени корней не обязаны быть попарно различными (Рисунок 2.8)

Дерево Фибоначчи - биномиальное дерево, где у каждой вершины удалено не более одного ребенка (Рисунок 2.7)

Рисунок 2.7: Дерево Фибоначчи высоты 4

Рисунок 2.8: Куча Фибоначчи

Вставка в кучу подразумевает добавление в список дерева степени 0 (дерево из одной вершины). Таким образом куча вырождается в список (Рисунок 2.9).

Рисунок 2.9: Вырожденная куча из 10 элементов

Объединение двух куч заключается в связывании крайних элементов двух куч. (Рисунок 2.10)

Рисунок 2.10: Добавления к исходной куче кучи 12-13-11

Для удаления из кучи вершины изменим ее значение ключа на -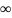 , и затем, чтобы восстановить свойства кучи просеем её к корневому списку. Если у удаляемой вершины есть дети, помещаем их к корневому списку. Далее начинается балансировка кучи, которая выполняется только при удалении, и нужна для того, чтобы куча не был вырождена в список. Суть балансировки заключается в следующем: берем две вершины степени n и объединяем их в дерево степени n+1, при этом в корне будет самый приоритетный из элементов, а менее приоритетный станет сыном. (Рисунок 2.11)

Рисунок 2.11: Куча после удаления элемента с ключом 11

Данная операция выполняется за логарифмическое время, но из-за того, что куча может быть частично или полностью вырождена в список появляется скрытая константа, из-за которой эффективность операции снижается.

Операция уменьшения значения ключа заключается в вырезании элемента из кучи, и вставке его в корневой список. В случае если новое значение ключа менее приоритетно чем у родителя, вырезание не производиться.

Преимущества кучи Фибоначчи над биномиальной в том, что операции, не требующие удаления, работают за константное время, а те что требуют удаления – за логарифмическое.

Кучи Фибоначчи обладают лучшей асимптотикой по сравнению с биномиальной и бинарной, но и в них есть один недостаток. Операция удаления зависит от сбалансированности кучи, и если мы часто добавляем элементы в кучу, и редко извлекаем, то её быстродействие ухудшается.

Были рассмотрены основные подходы к реализации очередей с приоритетом. Вопросом оптимизации куч Фибоначчи, направленных на уменьшение скрытой константы занялся Tadao Takaoka, который в своей работе Theory of 2-3 Heaps описал структуру данных, которая способна решить данную проблему.

3. Структура данных 2-3 куча

Основная проблема куч Фибоначчи заключалась в том, что балансировка кучи происходит только при удалении из кучи. Если бы мы смогли реализовать структуру данных, которая будет сохранять балансировку и при добавлении в кучу(слиянии), но при этом сохранив асимптотику, то удалось бы получить выигрыш в производительности. И эта структура – 2-3 куча.

2-3 куча — это массив 2-3 деревьев, определенных по индукции:

B₀ дерево состоит из одного или двух элементов

B_i дерево, состоит из B_i* + B_i-1

B_i* дерево, состоящее из B_i-1 + B_i-1 (Рисунок 3.1).

Рисунок 3.1: дерево 2-3 кучи

2-3 дерево - это сбалансированное дерево, родительский узел которого может иметь как два, так и три сына (Рисунок 3.2). 2-3 деревья относятся к деревьям и являются идеально сбалансированными. Высота дерева из n вершин лежит в диапазоне [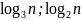 ] Однако 2-3 деревья из-за своей структуры занимают много памяти, так как фактическая информация храниться только в листьях, а узлы используются для адресации на нужный лист. В целях экономии произведем модификацию: Будем хранить данные по тому же принципу, что и в бинарных деревьях. Мы сможем себе это позволить в том случае если условимся объединять только деревья одной степени, что нам в принципе и надо.

На рисунках 7.1 и 7.2 приведен пример 2-3 дерева, и 2-3 дерева кучи:

Рисунок 3.2: 2-3 дерево

Раз мы ограничились в слиянии только деревьев одной степени, необходимо их классифицировать, и для этого введем два понятия:

Степень дерева – высота корневого узла

Насыщенность дерева – Наличие у корневого элемента партнерской связи (подробнее при описании структуры узла).

По насыщенности будем различать: насыщенные(t) и ненасыщенные(f) деревья. Тогда в куче будем xранить деревья по следующему принципу: в i ячейке дерева можно хранить только дерево степени i.

Как говорилось ранее дерево степени 0 содержит в себе или 1, или 2 вершины. Тогда в случае если дерево хранит 1 вершину, это ненасыщенное дерево степени 0(0f), а если 2 вершины, то это насыщенное дерево степени 0(0t). Насыщенное дерево при добавлении к нему вершин переходит в ненасыщенное более высокой степени. Дерево степени 1 будет хранить 3 или 6 вершин соответственно. Тогда насыщенное дерево степени n будет хранить в себе 3ⁿ вершин, а ненасыщенное 3ⁿ+3ⁿ = 2*3ⁿ вершин.

Таким образом насыщенное дерево является объединением двух ненасыщенных деревьев. Тогда максимальное количество элементов в куче из n деревьев выражается как 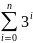. Примеры некоторых деревьев:

Таблица 2: Пример деревьев 2-3 кучи

Теперь самое время затронуть детали реализации и описать структуру узла 2-3 кучи (Рисунок 3.3):

Рисунок 3.3: Структура узла 2-3 кучи на примере 1f дерева

Где:

K (key) – ключ, определяет приоритет элемента

V (value) – значение, которое храниться вместе с ключом

pr (parent) – родительский узел, элемент с более высоким приоритетом

сh(child) – дочерний узел, элемент с более низким приоритетом

pt (partner) – партнерский узел. При объединении двух f деревьев они соединяются как партнеры. При этом узлы, подчиненные одному из партнеров непосредственно с другим партнером связей не имеют. Также имеет место нюанс: необходимо как-то помечать того партнера, который является более приоритетным. Во-первых, это позволит избежать лишних проверок при выполнении всех основных операций, во-вторых поможет избежать проблем при обходе кучи, в-третьих если партнер будет являться сыном, мы сразу будем знать по какому из них нужно возвращаться к родителю, и при этом ссылку на родителя у менее приоритетного элемента хранить не обязательно. Будем помечать самого приоритетного из двух соседей флагом sl(sister in law).Также для корневого элемента эта метка будет определять факт насыщенности дерева.

ln(left neighbor) – левый сосед

rn(right neighbor) – правый сосед

Необходимость соседской связи, и особенность реализации будет обозначена при описании алгоритма вставки.