5.2. Истечение пара или газа из сопловой решетки

П роцесс разгона пара в сопловой решетке связан с процессом его расширения. Процесс расширения пара в условиях адиабатного изменения параметров, представленный на рис.5.3, может быть выражен уравнением

где с_1а – осевая проекция абсолютной скорости потока на выходе из сопловой решетки, м/с;

с₀ – скорость потока перед сопловой решеткой, м/с;

Н₀ – располагаемый теплоперепад, Дж/кг; при с₀ ≈ 0 _.

Если выразить теплоперепад через параметры состояния с учетом адиабатного процесса, то последнее уравнение примет вид:

_,

где ε = р₁/р₀ - степень расширения пара в сопловой решетке.

Зная скорость движения рабочей среды можно найти объемный V (м³/с) и массовый G (кг/с) расход:

,

где f – площадь сечения перпендикулярное вектору скорости потока, м²;

v – удельный объем рабочей среды, м³/кг.

Учитывая, что расход рабочей среды (пара) в сопловой решетке не изменяется, получим

или

. (5.1)

Таким образом, площадь сечения межлопаточного канала проточной части турбины может, как увеличиваться, так и уменьшаться в зависимости от того, какое из слагаемых правой части равенства (5.1) дольше по абсолютной величине. Если увеличивать скорость (dc > 0), то можно увидеть, как при изменении скорости величина df/f поменяет свой знак, т.е. сечение до определенного момента будет уменьшаться (df < 0), а затем увеличиваться (df > 0). Скорость пара в наименьшем сечении называется критической скоростью и равна скорости звука: с_кр= а. Поэтому дозвуковой поток имеет место при сужающейся сопловой решетке и сверхзвуковой при расширяющейся.

Массовый расход рабочей среды (пара) для i-го сечения канала можно найти как

_.

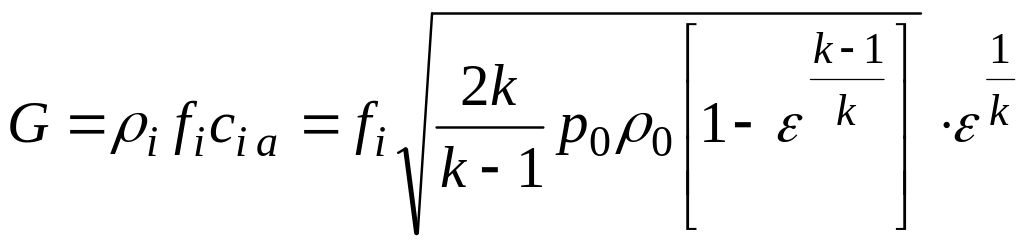О тсюда теоретически G = 0 при ε = 0 и ε = 1,0, однако, в реальных условиях при ε < 0,5 расход не изменяется, что и показано на графике рис.5.4. ε

Реальные скорости при движении по межлопаточному каналу от сечения 0-0 до 1-1 уменьшаются с учетом величины потерь на трение на завихрения и т.д. Величину реальной скорости в сечении 1-1 можно определить по уравнению с₁ = φс₀ при условии, что сечение канала не изменяется. Здесь φ – коэффициент скорости; обычно φ = 0,96 ÷ 0,98.

5.3. Процесс движения рабочей среды в каналах направляющих и рабочих решеток

Процесс движения рабочей среды в рабочей решетке отличается от процесса в сопловой тем, что сама решетка, лопатки, из которых она состоит, и межлопаточный канал, в котором движется рабочая среда, вращаются вокруг оси с окружной скоростью и. Поэтому процессы в рабочей решетке можно рассматривать относительно подвижной (относительное движение) и неподвижной (абсолютное движение) систем координат. На рис.5.5 показано схематическое представление относительного (векторы w₁ и w₂) движения пара в межлопаточном канале рабочей решетки, абсолютное (векторы с₁ и с₂) и окружное (вектор и).

Векторное построение абсолютной, относительной и окружной скоростей называется треугольником скорости.

В теории турбомашин входной и выходной треугольники скоростей рассматриваются приведенными к одной точке, как это показано на рис.5.6. На рис.5.6,а представлены треугольники скоростей активной ступени давления, а на рис.5.6,б - реактивной ступени давления со степенью реактивности ρ = 0,5. В активной ступени давления степень реактивности ρ = 0 или близко к нулю. Степенью реактивности называется отношение теплоперепадов, перерабатываемых в рабочей решетке к общему теплоперепаду ступени (рис.5.7):

,

где h_р – теплоперепад, срабатываемый в рабочей решетке; h_р = h₁ - h₂, Дж/кг;

h_н – теплоперепад, перерабатываемый в направляющей решетке: h_н = h₀ – h₁, Дж/кг;

h₀ – энтальпия рабочей среды на входе в направляющую решетку, Дж/кг;

h₁ – энтальпия среды на входе в рабочую решетку ступени, Дж/кг;

h₂ – энтальпия среды на выходе из рабочей решетки, Дж/кг;

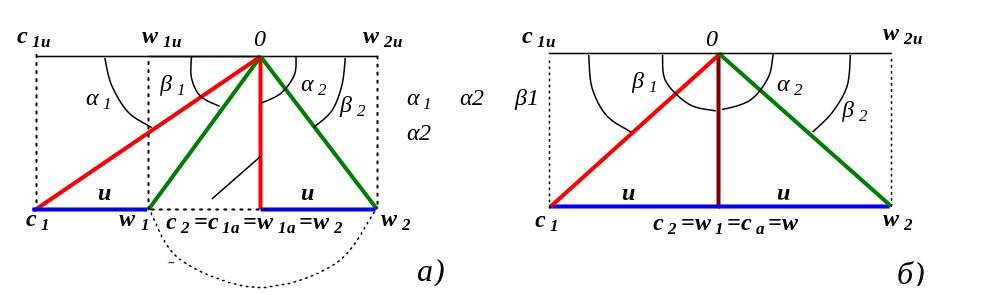
Рис.5.6. Приведенные треугольники скоростей активной (а) и реактивной (б) ступени давления турбомашины

На рис.5.7 представлены теплоперепады энтальпий в активной (рис.5.7,а) и реактивной (рис.5.7,б) ступенях давления турбомашины. Из рис.5.7,а видно, что в направляющей решетке активной ступени давления турбины полная энтальпия h₀ сохраняется неизменной при уменьшении статической энтальпии рабочей среды от h₀ до h₁, за счет этого происходит увеличение скорости от с₀ до с₁. В рабочей решетке производится механическая работа при неизменном давлении за счет уменьшения скорости от с₁ до с₂. В hs – диаграмме удобно анализировать потери в направляющей Δh_н и рабочей Δh_р решетках. Они происходят с увеличением энтропии s при адиабатическом процессе. В реактивной ступени давления турбины (рис.5.7,б) изменения полной h и статической h энтальпий происходит как в направляющей, так и в рабочей решетках. При этом в этих решетках происходит последовательное изменение давления и скорости рабочей среды.

Рис.5.7. Теплоперепады активной (а) и реактивной (б) ступеней давления турбины в hs – диаграмме

Рабочий процесс в направляющей решетке описывается следующим уравнением (рис.5.7)

,

где с₀, с₁, с_1t – скорости рабочей среды на входе в решетку и на выходе из нее реальную и идеальную (теоретическую) соответственно, м/с;

φ – коэффициент скорости, учитывающий потери в направляющей решетке; с₁= φ с_1t;

h_1t – энтальпия на выходе из направляющей решетки при движении рабочей среды в ней без потерь, Дж/кг.

Рабочий процесс в рабочей решетке турбины можно выразить уравнением (рис.5.7)

,

где w₁, w₂, w_2t – скорости рабочей среды на входе в рабочую решетку и на выходе из нее реальную и идеальную (теоретическую) соответственно, м/с;

u₁, u₂ – окружные скорости колеса на входе и выходе рабочей решетки, м/с;

– коэффициент скорости, учитывающий потери в рабочей решетке; с₁= с_1t;

h_2t – энтальпия на выходе из рабочей решетки при движении рабочей среды в ней без потерь, Дж/кг.

Суммарный реальный теплоперепад в ступени турбины с учетом двух предыдущих формул определяется по уравнению (рис.5.7)

. (5.2)

В турбинных ступенях, как правило, принимается с₀ ≈ с₂ (смотри треугольники скоростей (рис.5.6)). В осевых турбинах u₁ = u₂, поэтому трете слагаемое правой части уравнения исчезает.

Общий теплоперепад определяемый в уравнении (5.2) и может быть использован в качестве определения удельной механической работы турбинной ступени

.

Из треугольников скоростей (рис.5.6) получаем:

Отсюда уравнение удельной работы турбинной ступени давления можно представит в виде уравнения Эйлера

.

Мощность ступени давления турбины, Вт, определяется по уравнению

,

где G – расход рабочей среды в проточной части турбины, кг/с.

Процесс турбинной ступени хорошо анализировать в hs-диаграмме на предмет ее экономичности (рис.5.7,б):

,

где - потери с выходной скоростью, Дж/кг; = ;

Н₀, Нi – располагаемый и внутренний теплоперепады ступени, Дж/кг.

Учитывая последнее уравнение, можно определить относительный внутренний к.п.д. ступени турбины

.

Таким образом, процессы в каналах рабочих и направляющих решетках анализируются с помощью треугольников скоростей и перепадов энтальпий в hs-диаграмме.