6. Обратная матрица

Определение. Матрица называется обратной для матрицы , если она вместе с удовлетворяет условию: , где – единичная матрица.

Определение. Квадратная матрица называется невырожденной, если . Если , то называется вырожденной.

Пример. по свойству 6 определителей, то есть – вырожденная.

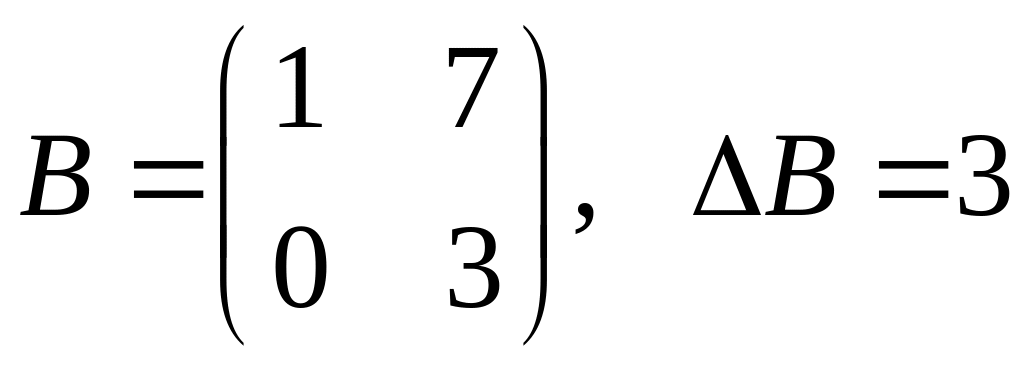, значит, – невырожденная.

Теорема. Всякая невырожденная матрица имеет обратную, причем одну.

Обратная матрица для матрицы - го порядка имеет вид:

.

Пример. Найти матрицу, обратную для .

=3 существует.

Проверка:

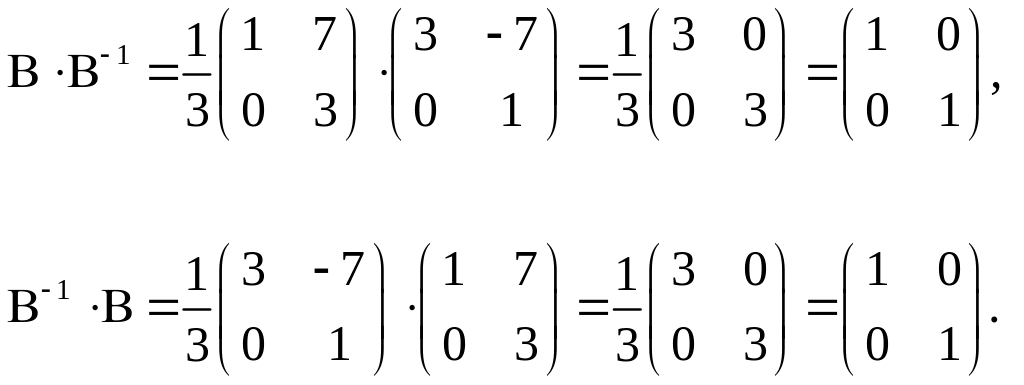
7. Ранг матрицы.

Определение. Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы.

Обозначение: rangА, или r (А).

Из определения следует:

а) ранг матрицы А_тхп не превосходит меньшего из ее размеров,

т.е. r (А).≤min(т;п)

б) r(А) = 0 тогда и только тогда, когда все элементы матрицы равны нулю,

т.е. А =0;

в) для квадратной матрицы n-го порядка r ≥п тогда и только тогда, когда матрица А - невырожденная.

Теорема. Ранг матрицы не изменяется при элементарных преобразованиях.

С помощью элементарных преобразований можно привести матрицу к так называемому ступенчатому виду, когда вычисление ее ранга не представляет труда.

Определение: Матрица А называется ступенчатой, если она имеет вид:

Замечание. Условие r≤k всегда может быть достигнуто транспонированием матрицы.

Очевидно, что ранг ступенчатой матрицы равен r, так как имеется минор r-го порядка, не равный нулю:

Пример: Определить ранг матрицы

Решение: Все миноры третьего порядка равны нулю, т.к. каждый определитель содержит нулевой столбец.

Есть минор второго порядка, отличный от нуля

Следовательно, ранг r(A)=2.

Лекция №2 Тема: Решение систем линейных уравнений

План:

1. Общие понятия системы линейных уравнений.

2. Формулы Крамера.

3. Метод обратной матрицы.

4. Метод Гаусса.

1. Общие понятия системы линейных уравнений.

Определение. Система m уравнений с n неизвестными в общем виде записывается следующим образом:

,

где a_ij – коэффициенты, а b_i – постоянные.

Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество.

Определение. Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной.

Определение. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного.

Определение. Для системы линейных уравнений матрица

А = называется матрицей системы, а матрица

А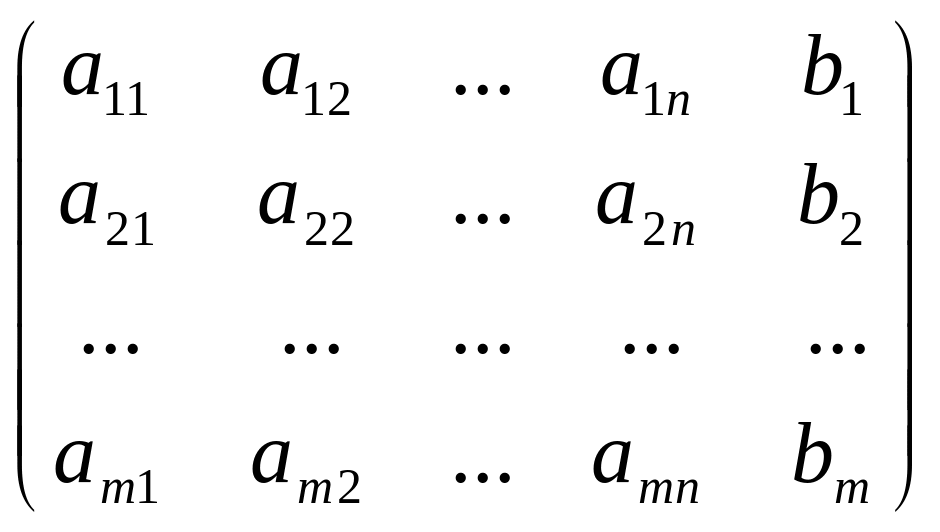^*= называется расширенной матрицей системы

Определение. Если b₁, b₂, …,b_m = 0, то система называется однородной. Замечание. Однородная система всегда совместна, т.к. всегда имеет нулевое решение.

Элементарные преобразования систем.

1. Прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на одно и то же число, не равное нулю.

2. Перестановка уравнений местами.

3. Удаление из системы уравнений, являющихся тождествами для всех х.