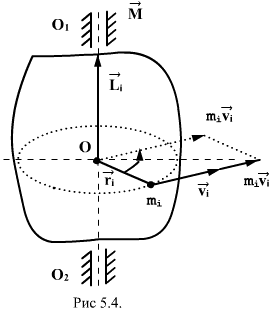
12. Момент импульса для материальной точки. Момент импульса материальной точки массой m, движущейся с постоянной по величине скоростью V по окружности радиуса r.

Момент импульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение. Момент импульса материальной точки относительно точки O определяется векторным произведением , где r — радиус-вектор, проведенный из точки O, p=mv — импульс материальной точки. Момент импульса материальной точки относительно неподвижной оси L_z равен проекции на эту ось вектора момента импульса, определенного относительно произвольной точки O данной оси. Значение момента импульса L_x не зависит от положения точки O на оси z. Векторное произведение радиуса-вектора r_i материальной точки на ее импульс: m_iv_i называют моментом импульса L_i, этой точки относительно точки О L_i=[r_i,m_i,v_i]. Вектор L_i иногда называют также моментом количества движения материальной точки. Он направлен вдоль оси вращения перпендикулярно плоскости, проведенной через векторы r_i  и m_iv_i и образует с ними правую тройку векторов (при наблюдении из вершины вектора видно, что вращение по кратчайшему расстоянию от r_i к m_iv_i происходит против часовой стрелки).Векторную сумму моментов импульсов L_i всех материальных точек системы называют моментом импульса (количества движения) L системы относительно точки О:

Векторы r_i и mivi взаимно перпендикулярны и лежат в плоскости перпендикулярной оси вращения тела. Поэтому L_i=r_im_iv_isina=r_im_iv_i. С учетом связи линейных и угловых величин и направлен вдоль оси вращения тела в ту же сторону, что и вектор  . Таким образом

13. Момент силы и момент импульса частицы относительно полюса. Уравнение моментов относительно полюса. Момент импульса и момент силы относительно оси. Уравнение моментов относительно оси.

Момент сил и момент импульса относительно неподвижного начала. Пусть O какая-либо неподвижная точка в инерциальной системе отсчета. Ее называют началом или полюсом. Моментом силы F относительно точки O называется вектор произведения радиус-вектора r на силу F : , M=rFsina . Моментом Mнескольких сил относительно точки называется сумма моментов этих сил относительно этой же точки  . Моментом импульса материальной точки относительно точки О называется вектор произведения радиус-вектора   на импульс   :   . Для системы m материальных точек моментом импульса относительно неподвижной точки O называется сумма моментов импульсов этих точек относительно того же начала:

 

Уравнение моментов относительно полюса. Предположим, что точка O неподвижна в случае одной материальной точки, дифференцируя равенство   , получаем:  . При неподвижной точке O 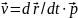 , поэтому   , кроме того   , т.о. 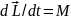  - это уравнение моментов для одной материальной точки. Для системы материальных точек, в которой L определяется выражением , а M - выражением  , для внешних сил уравнение моментов имеет вид: 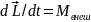  . Моментом импульса системы относительно оси называется проекция на эту ось вектора момента импульса системы относительно любой точки, выбранной на рассматриваемой оси. Выбор точки на оси влияет на значения моментов импульса M и L относительно точки, но не влияет на значения соответствующих проекций моментов на эту ось. Если выбираем прямоугольную систему координат с началом, совпадающим с полюсом, то к L и M приписывается с низу ось.

Момент импульса и момент силы относительно оси. Уравнение моментов относительно оси.

В озьмем в интересующей нас системе отсчета произвольную неподвижную ось Z. Пусть относительно некоторой т. О этой оси момент импульса частицы равен 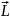 , а момент сил  .Моментом импульса частицы относительно оси Z называется проекция на эту ось вектора   , определенного относительно произвольной точки О данной оси. Аналогично вводится понятие момента силы 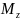 относительно оси Z. Величины  и  не зависят от выбора т. О на оси  . Уравнение моментов относительно оси z: 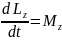 , т.е. производная момента импульса относительно оси Z равна моменту силы относительно этой оси. В частности, при 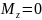 момент импульса  . Т.е., если момент силы относительно некоторой оси Zравен 0, то L относительно этой оси остается постоянным. При этом вектор  может изменяться.