5. Масса. Сила. Центральные, консервативные, диссипативные силы. Принцип суперпозиции сил. Примеры.

Масса — скалярная физическая величина, одна из важнейших величин в физике. Первоначально (XVII—XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе (инертность), так и гравитационные свойства — вес. В современной физике понятие «количество вещества» имеет другой смысл, а масса тесно связана с понятиями «энергия» и «импульс» (по современным представлениям — масса эквивалентна энергии покоя). Масса проявляется в природе несколькими способами.

• Пассивная гравитационная масса показывает, с какой силой тело взаимодействует с внешними гравитационными полями — фактически эта масса положена в основу измерения массы взвешиванием в современной метрологии.

• Активная гравитационная масса показывает, какое гравитационное поле создаёт само это тело — гравитационные массы фигурируют в законе всемирного тяготения.

• Инертная масса характеризует инертность тел и фигурирует в одной из формулировок второго закона Ньютона. Если произвольная сила в инерциальной системе отсчёта одинаково ускоряет разные исходно неподвижные тела, этим телам приписывают одинаковую инертную массу.

Сила — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нём деформаций и напряжений.

Ц ентральная сила — сила, линия действия которой при любом положении тела, к которому она приложена, проходит через точку, называемую центром силы{\displaystyle K}. Примерами центральных сил являются силы тяготения и Кулона, направленные вдоль линии, соединяющей точечные массы или точечные заряды. Проще всего центральные силы вводятся для физических систем, состоящих из конечного числа объектов, размерами которых можно пренебречь (материальных точек), или, иногда, некоторых эквивалентных им, состоящих из протяжённых объектов с фиксированной внутренней структурой. Распределенные системы, в которых действуют центральные силы, в общем случае не могут быть представлены конечным количеством материальных точек. В случае распределённых систем общим подходом является разбиение их на очень большое (в пределе бесконечное) количество элементов малого (в пределе стремящегося к нулю) размера каждый (которые и рассматриваются как материальные точки), между которыми действуют центральные силы в соответствии с определением, данным выше. Таким образом, в этом случае центральной, собственно, является каждая элементарная сила, а реальная сила является суммой (суперпозицией) таких элементарных сил. Классическая физика вводит также понятие поля центральной силы для области трёхмерного пространства, в котором действуют центральные силы.

• Для любой центральной силы {\displaystyle {\vec {F}}}F выполняется соотношение 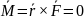{\displaystyle {\vec {M}}={\vec {r}}\times {\vec {F}}=0,} , где M - момент сил, {\displaystyle {\vec {r}}}r — радиус-вектор с началом в центре силы), свидетельствующее о равенстве нулю момента силы относительно центра силы. В физике консервативные силы (потенциальные силы) — это силы, работа которых не зависит от вида траектории, точки приложения этих сил и закона их движения, и определяется только начальным и конечным положением этой точки. Равносильным определением является и следующее: консервативные силы — это такие силы, работа которых по любой замкнутой траектории равна 0. В теоретической физике выделяют только четыре типа сил, каждая из которых является консервативной. В школьной программе по физике силы разделяют на консервативные и неконсервативные. Примерами консервативных сил являются: сила тяжести, сила упругости, сила кулоновского взаимодействия. Примером неконсервативной силы является сила трения. Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется.

Д ля консервативных сил выполняются следующие равенства:

{\displaystyle \int \limits _{C_{1}}{\vec {F}}\cdot {\vec {dl}}=\int \limits _{C_{2}}{\vec {F}}\cdot {\vec {dl}}} — работа, производимая консервативной силой, определяется только начальным и конечным положением точки её приложения и не зависит от выбора траектории, по которой перемещается тело. {\displaystyle \oint \limits _{C}{{\vec {F}}d{\vec {l}}}=0} — работа консервативных сил по произвольному замкнутому контуру равна 0; {\displaystyle \nabla \times {\vec {F}}=0} — ротор консервативных сил равен 0; {\displaystyle {\vec {F}}=\nabla U}— консервативная сила является градиентом некой скалярной функции {\displaystyle U}U , называемой силовой. Эта функция равна потенциальной энергии{\displaystyle E_{p},}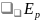  взятой с обратным знаком. Соответственно,  {\displaystyle {\vec {F}}} и  {\displaystyle E_{p}} связаны соотношением . 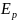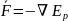{\displaystyle {\vec {F}}=-\nabla E_{p}.}Таким образом, потенциальная сила всегда направлена в сторону уменьшения потенциальной энергии.Диссипативные силы — силы, при действии которых на механическую систему её полная механическая энергия убывает (то есть диссипирует), переходя в другие, немеханические формы энергии, например, в теплоту. В отличие от потенциальных сил зависят не только от взаимного расположения тел, но и от их относительных скоростей.

Принцип суперпозиции один из самых общих законов во многих разделах физики. В самой простойформулировке принцип суперпозиции гласит:

• результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этихсил.

Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что напряженностьэлектростатического поля, создаваемого в данной точке системой зарядов, есть сумманапряженностей полей отдельных зарядов.

Принцип суперпозиции может принимать и иные формулировки, которые полностью эквивалентны приведённой выше:

• Взаимодействие между двумя частицами не изменяется при внесении третьей частицы, такжевзаимодействующей с первыми двумя.

• Энергия взаимодействия всех частиц в многочастичной системе есть просто сумма энергий парныхвзаимодействий между всеми возможными парами частиц. В системе нет многочастичныхвзаимодействий.

• Уравнения, описывающие поведение многочастичной системы, являются линейными по количеству частиц.

Именно линейность фундаментальной теории в рассматриваемой области физики есть причинавозникновения в ней принципа суперпозиции. Пример: Принцип суперпозиции полей.

Р езультат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.

 Принцип суперпозиции полей, или принцип наложения, является условностью, согласно которой некоторый сложный процесс взаимодействия между определённым числом объектов можно представить в виде суммы взаимодействий между отдельными объектами. Принцип суперпозиции применим лишь к тем системам, которые описываются линейными уравнениями. Графически принцип суперпозиции полей можно представить в виде геометрической суммы векторов силы, которые действуют на пробный заряд, помещённый в поле точечных электрических зарядов.

  Если поле создано простейшей совокупностью зарядов, которая состоит из положительного и отрицательного зарядов, находящихся на некотором расстоянии друг от друга, то результирующее поле в точке наблюдения находится с помощью правила параллелограмма. Нельзя применять принцип суперпозиции к взаимодействию атомов и молекул между собой. Например, если взять два атома, у которых электроны находятся во взаимодействии, и поднести к ним третий такой же атом. Часть электронов от первых двух атомов притянется и вступит во взаимодействие с третьим атомом. Т.е. первоначальное распределение энергии в системе изменится. Изначальная сила взаимодействия между электронами и ядрами первых двух атомов уменьшится. Т.е. третий атом влияет не только на электроны, но и на ядра атомов. Также принцип суперпозиции нельзя применять для нелинейных систем.