31. Закон Био-Савара-Лапласа для магнитной индукции поля, создаваемого элементом тока. Принцип суперпозиции магнитных полей.

Закон Био-Савара-Лапласа для проводника с током I, элемент dl которого создает в некоторой точке A индукцию поля dB, записывается в виде: 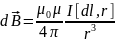, где dl – вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током; r – радиус-вектор, проведенный из элемента проводника в точку A исследуемого поля, r – модуль радиуса-вектора ; μ₀ –магнитная постоянная (4π10^-7 Гн/м); μ – магнитная проницаемость среды, которая в воздухе и в вакууме равна единице. Направление dB перпендикулярно и, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление враще­ния головки винта дает направление, если поступательное движение винта соответ­ствует направлению тока в элементе.

Модуль вектора определяется выражением 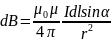, где α – угол между векторами и. Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности: . Расчет характеристик магнитного поля (и H) по приведенным формулам в общем случае сложен. Однако если распределение тока имеет определенную сим­метрию, то применение закона Био-Савара-Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля.

32. Магнитное поле, создаваемое равномерно движущимся зарядом.

Каждый проводник с током создает в ок­ружающем пространстве магнитное поле. Электрический же ток представляет собой упорядоченное движение электрических зарядов. Поэтому можно сказать, что лю­бой движущийся в вакууме или среде за­ряд создает вокруг себя магнитное поле. В результате обобщения опытных данных был установлен закон, определяющий по­ле В точечного заряда Q, свободно движу­щегося с нерелятивистской скоростью v. Под свободным движением заряда по­нимается его движение с постоянной ско­ростью.

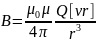
где r — радиус-вектор, проведенный от за­ряда Q к точке наблюдения М. Согласно выражению, вектор В направлен перпендикулярно плоскости, в которой расположены векторы v и г, а именно: его направление совпадает с на­правлением поступательного движения правого винта при его вращении от v к г. Модуль магнитной индукции вычисляется по формуле

33. Сила Лоренца. Движение заряда по окружности в постоянном магнитном поле.

Сила Лоренца всегда перпендикулярна скорости движения заряда. Это означает, что сила Лоренца не может изменить величину скорости движения, но изменяет её направление. Поэтому в однородном магнитном поле заряд, влетевший в магнитное поле перпендикулярно его силовым линиям, будет двигаться по окружности. Если на заряд действует только сила Лоренца, то движение заряда подчиняется следующему уравнению, составленному на основе второго закона Ньютона: ma=F_л. Поскольку сила Лоренца перпендикулярна скорости, постольку ускорение заряженной частицы является центростремительным (нормальным): a=v²/R(здесьR – радиус кривизны траектории заряженной частицы). Используя выражение для расчёта ускорения и заменив F_лнаqvB, получаем mv²/R=qvB. Отсюда следует, что радиус окружности, по которой будет двигаться заряд в однородном магнитном поле, равен R=mv/qB.

Если заряженная частица влетит в однородное магнитное поле под углом к силовым линиям, то её траектория будет более сложной.

Для того чтобы установить форму траектории и её параметры, разложим скорость частицы на две компоненты – параллельную v_|| =vcosи перпендикулярную v_=vsin силовым линиям магнитного поля. Компонента скорости v_||не изменяется, так как сила Лоренца не действует на заряженную частицу, движущуюся параллельно силовым линиям магнитного поля. За счёт этой компоненты заряд будет равномерно двигаться вдоль силовых линий.

К омпонента скорости v_ не будет меняться по величине, но будет непрерывно изменяться её направление. За счёт этой компоненты заряд будет двигаться по окружности, плоскость которой перпендикулярна силовым линиям. Заряженная частица одновременно будет участвовать в этих движениях, поэтому её траектория будет представлять собой винтовую линию. Период обращения заряженной частицы равен времени, за которое она пройдёт один виток, T=2πR/ v_.

Шаг винтовой линии равен расстоянию, которое заряд пройдёт за один период: L=v_||T.