
- •Тести з навчальної дисципліни „Вища математика”
- •1 Курс «Економіка і підприємництво» («Облік та аудит, «Економіка підприємства», «Фінанси та кредит»)
- •1,2 Семестри, теми 1 -7
- •Тема 1. Елементи теорії матриць і визначників
- •Тема 2. Загальна теорія систем лінійних алгебраїчних рівнянь.
- •Тема 3. Елементи векторної алгебри та аналітичної геометрії.
- •Тема 4. Елементи теорії границь
- •Тема 5. Диференціальне числення функції однієї змінної.
- •Тема 6. Дослідження функцій та побудова їх графіків.
- •Тема 7. Основні поняття функції багатьох змінних
- •Тема 8. Інтегральне числення.
- •Тема 9. Економічна динаміка та її моделювання: диференціальні та різницеві рівняння.
- •Тема 10. Ряди та їх застосування.
Тема 3. Елементи векторної алгебри та аналітичної геометрії.
Вектори
задані координатами
|
|
|
* |
|
Коли вектори на площині будуть перпендикулярні?: |
їх скалярний добуток дорівнює одиниці |
їх скалярний добуток дорівнює добутку модулів цих векторів |
*їх скалярний добуток дорівнює нулю |
їх скалярний добуток не можна» знайти |
Чому
дорівнює векторний добуток двох
векторів
|
* |
|
|
|
Векторний
добуток одиничних векторів
|
|
* |
|
|
Векторний
добуток ортів ̃ |
* |
|
|
|
Вкажіть
рівність, яка виконується для векторного
добутку двох векторів
|
|
|
= - |
*
=- |
Коли два вектори вважаються рівними? |
їх модулі рівні |
напрями збігаються |
*напрями збігаються, а модулі рівні |
модулі рівні, а напрям протилежний |
Як називаються два вектори, які лежать в одній площині або в паралельних площинах? |
спів напрямленими |
колінеарними |
*компланарними |
ортогональними |
Як називаються два вектори, які лежать на одній прямій? |
*колінеарними |
компланарними |
спів напрямленими |
ортогональними |
Є
вектор
|
одержимо нуль – вектор |
напрям вектора |
*протилежний вектору |
перпендикулярний вектору |
З означення векторного добутку вкажіть правильну властивість таких векторів? |
∙ |
∙ = - |
∙ = + |
* ∙ = - ∙ |
Є вектор і число =3. Який напрямок буде мати вектор ? |
одержимо нуль – вектор |
*напрям вектора |
протилежний вектору |
перпендикулярний вектору |
Знайдіть правильну відповідь для скалярного добутку двох векторів і |
|
|
|
* |
Чому дорівнює довжина вектора заданого координатами (3;5)? |
*6 |
5 |
4 |
8 |
Косинус кута між двома векторами і визначається формуло? |
|
* |
+ |
|
За
якою формулою обчислюється модуль
вектора
|
* |
|
|
|
Назвіть правильну відповідь для векторного добутку двох векторів і ? |
|
|
|
* |
Яким співвідношенням пов’язані паралельні вектори? |
* |
|
|
|
Які вектори називають протилежними? |
колінеарні і однакової довжини |
однакової довжини і колінеарні |
протилежно спрямовані |
*колінеарні, однакової довжини і протилежно спрямовані |
Розглянемо
вектор
|
* |
|
|
|
За
якою формулою обчислюється скалярний
добуток векторів
|
|
* |
|
|
Чому
дорівнює скалярний добуток одиничних
векторів
|
*0 |
1 |
-1 |
2 |
Чому
дорівнює скалярний добуток ортів
|
|
* |
|
|
Чому чисельно дорівнює векторний добуток двох векторів ? |
подвійна площа паралелограма, побудованого на цих векторах |
площі трикутника |
*площі паралелограма, побудованого на векторах |
площі кола, радіус якого дорівнює довжині вектора |
Чому дорівнює векторний добуток двох векторів? |
додатному числу |
від'ємному число |
сумі векторів |
*вектору |
Чому дорівнює добуток вектора на число λ, якщо =(3,-2,4) а λ=2 |
|
(5, 0, -4) |
*(6, -4, 8) |
(1, 0, 2) |
Чому дорівнює скалярний добуток двох векторів і , якщо = ? |
2 |
1 |
+ |
* |
Яка ознака колінеарності векторів , ? |
|
|
* |
|
Яка рівність виконується для векторного добутку двох векторів , ? |
|
|
|
*
=- |
Що
визначає будь-яке рівняння першого
ступеня відносно
|
поверхню |
лінію |
*площину |
півплощину |
Вказати
рівняння лінії, яка утворює з віссю
ОХ кут
|
* |
|
|
|
Вказати
рівняння лінії, яка утворює кут
з віссю
|
|
|
* |
|
Вказати
формулу відстані від точки
|
|
|
|
* |
Вказати
формулу відстані між двома точками
|
* |
|
|
|
Вказати рівняння прямої, яка проходить через точку А (2, -1) і паралельна осі ОУ? |
х = -1 |
*х = 2 |
у = -1 |
у = 2 |
Вкажіть загальне рівняння прямої на площині? |
|
|
|
* |
Знайдіть рівняння прямої, яка паралельна осі ОХ? |
|
* |
|
|
Вкажіть рівняння прямої, яка паралельна осі ОУ? |
* |
|
|
|
Знайдіть загальне рівняння прямої, яка проходить через початок координат? |
* |
|
|
|
Запишіть рівняння прямої, що паралельна осі ОХ і проходить через точку А = (-3, 2) ? |
|
|
* |
|
Що означає геометричний зміст k в рівнянні прямої y=kx+b? |
Це відрізок, який відтинає пряма на осі координат |
Це відрізок, який відтинає пряма на осі абсцис |
Це тангенс кута, утвореного прямою з віссю ОY |
*Це тангенс кута, утвореного прямою з додатнім напрямком осі ОХ |
Дві прямі задані загальним рівнянням. При якій умові вони будуть паралельні? |
|
* |
|
|
Дві прямі задані загальним рівнянням. При якій умові вони будуть перпендикулярні? |
|
|
* |
|
Дві прямі паралельні, то яким співвідношенням пов’язані їх кутові коефіцієнти K1 і K2? |
K1>K2 |
K1<K2 |
* |
K1∙K2=1 |
Довжина
відрізка між двома точками з координатами
|
|
|
|
* |
Яке рівняння відповідає загальному рівнянні площини у просторі ? |
* |
|
|
|
Записано
дві прямі:
|
*прямі перпендикулярні. |
прямі паралельні. |
прямі перетинаються під гострим кутом. |
правильної відповіді немає. |
Маємо
рівняння кола
|
|
|
|
* |
Запишіть канонічне рівняння гіперболи? |
|
* |
|
|
Запишіть канонічне рівняння еліпса? |
|
|
|
* |
Чому дорівнює канонічне рівняння параболи, віссю симетрії якої є вісь ОУ? |
|
|
* |
|
Чому дорівнює канонічне рівняння параболи, віссю симетрії якої є вісь ОХ? |
|
|
|
* |
Координати
середини відрізка
|
|
* |
|
|
Координати точки , що ділить відрізок у заданому відношенні , знаходяться за формулами? |
|
|
* |
|
Назвіть рівняння прямої у відрізках на осях? |
|
* |
|
|
Вкажіть
рівняння прямої, що проходить через
дві задані точки
|
|
|
|
* |
Назвіть
рівняння прямої, що проходить через
задану точку з координатами
|
* |
|
|
|
Вкажіть рівняння прямої, що проходить через точку з координатами (2, 4)? |
* |
|
|
|
Відносно
якої осі симетрична парабола
|
*осі ординат |
осі абсцис |
бісектриси І і ІІІ координатних кутів |
прямої
|
Відносно
якої осі симетрична парабола
|
прямої
|
*прямої |
прямої
|
прямої
|
Нехай
пряма проходить через точки
|
|
|
* |
|
Пряма
проходить через точку
|
|
* |
|
|
Назвіть
рівняння
, де
|
параболи |
*гіперболи |
еліпса |
кола |
Назвіть рівняння , де ? |
параболи |
кола |
гіперболи |
*еліпса |
Оберіть
рівняння кола з центром в точці
|
|
* |
|
|
Як пряма орієнтована відносно осей координат, якщо її рівняння AX+BY=0? |
Пряма, що відтинає на осі ОХ відрізок А |
пряма , що відтинає на осі ОY відрізок B |
пряма , що паралельна осі ОХ |
*пряма , що проходить через початок координат |
Яку
криву описує рівняння: |
коло |
*еліпс |
гіперболу |
параболу |
Якщо
в загальному рівнянні другого порядку
|
еліпса |
*кола |
гіперболи |
параболи |
Якщо в рівнянні коефіцієнти А і В різних знаків, то яку фігуру описує це рівняння? |
еліпса |
кола |
*гіперболи |
параболи |
Якщо в рівнянні коефіцієнти А і В одного знаку, але не рівні, то яку фігуру описує це рівняння? |
*еліпса |
кола |
гіперболи |
параболи |
Якщо дві прямі паралельні, то яким співвідношенням пов’язані їх кутові коефіцієнти K1 і K2? |
K1>K2 |
K1<K2 |
*К1 = К2 |
K1*K2=1 |
Якщо прямі паралельні, то якому співвідношенню задовольняють їх кутові коефіцієнти? |
|
* |
|
|
Якщо прямі перпендикулярні то якому співвідношенню задовольняють їх кутові коефіцієнти ? |
|
|
|
* |
Як пряма BY+С=0 орієнтована відносно осей координат ? |
*пряма паралельна осі ОХ |
пряма паралельна осі ОY |
пряма проходить через початок координат |
пряма перетинає вісь ОX |
Як пряма АХ+С=0 орієнтована відносно осей координат на площині? |
пряма проходить через початок координат |
пряма паралельна осі ОХ |
*пряма паралельна осі ОY |
пряма перетинає вісь ОY |
Якщо в рівнянні, , А = 0, або В = 0, то якої фігури це рівняння? |
еліпса |
кола |
гіперболи |
*параболи |
Як називають вектор, у якого початок і кінець збігаються? |
початковим |
*нульовим |
одиничним |
компланарним |
Мішаним
добутком векторів
|
*дорівнює
скалярному добутку вектора
|
дорівнює простому добутку вектора на векторний добуток векторів і |
дорівнює векторному добутку вектора на векторний добуток векторів і |
дорівнює сумі вектора і |
Вкажіть властивість мішаного добутку? |
* |
|
|
Немає вірної відповіді |
Вкажіть канонічне рівняння прямої у просторі? |
* |
|
|
Немає вірної відповіді |

 ,
,
 ,
яка властивість векторів, якщо вони
колінеарні?
,
яка властивість векторів, якщо вони
колінеарні?

 ;
;


 ?:
?:





 дорівнює відповідно
дорівнює відповідно



 самих на себе дорівнює
самих на себе дорівнює





 ,
,
 :
:
 =
+
=
+

 і число
=-3.
Який напрямок буде мати вектор
і число
=-3.
Який напрямок буде мати вектор
 ?
? =
∙
=
∙







 ?
?







 ,
(
-
дійсне число)
,
(
-
дійсне число)

 =0
=0 ,
початок якого збігається з початком
координат, а кінець з точкою
,
початок якого збігається з початком
координат, а кінець з точкою
 .
Якій запис називається Розкладом
вектора
.
Якій запис називається Розкладом
вектора
 в базисі
в базисі
 ?
?




 і
і
 ?
?



 ?
? системи координат самих на себе?
системи координат самих на себе?










 =
+
=
+
 =
-
=
-

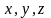 геометрично?
геометрично? і проходить через точку А = (-5, 5)
і проходить через точку А = (-5, 5)



 і проходить через точку А (2,-2).
і проходить через точку А (2,-2).



 до прямої, якщо пряма задана загальним
рівнянням?
до прямої, якщо пряма задана загальним
рівнянням?



 і
і
 на площині?
на площині?






















 і
(
і
( )
за якою формулою визначається?
)
за якою формулою визначається?





 як вони взаємно розташовані на площині?
як вони взаємно розташовані на площині? .
Вкажіть координати центра кола і його
радіус?
.
Вкажіть координати центра кола і його
радіус? ,
,
 ,
, ,
, ,
,









 визначаються формулою?
визначаються формулою? ,
,

 ,
,

 ,
,

 ,
,

 ;
;
 ;
; ;
;

 ;
;

 ;
;




 і
і
 ?
?


 .
. ?
?







 ?
?
 ?
?


 і
і
 .
Назвіть рівняння прямої у відрізках?
.
Назвіть рівняння прямої у відрізках?



 і утворює з віссю ОХ
кут
.
Написати рівняння прямої?
і утворює з віссю ОХ
кут
.
Написати рівняння прямої?



 :?
:? ?
?


 ?
? коефіцієнти
А і В одного знаку і рівні, то яку фігуру
описує це рівняння?
коефіцієнти
А і В одного знаку і рівні, то яку фігуру
описує це рівняння?







 називається число, що відповідає
умові?
називається число, що відповідає
умові? на векторний добуток векторів
і
на векторний добуток векторів
і






